高三数学第二次诊断性考试
高三数学试题(文科)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分。考试时间120
分钟。
2.考生一律不准使用计算器。
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合P={1,2,3,4,5},集合![]() ,那么下列结论正确的是( )
,那么下列结论正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知![]() “m≠0”是“mn≠0”的 ( )
“m≠0”是“mn≠0”的 ( )
A.必要但不充分条件 B.充分但不必要条件
C.充要条件 D.即不充分也不必要条件
3.下列不等式中解集为实数集R的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.在等差数列![]() 中,有
中,有![]() ,则此数列的前13项之和为 ( )
,则此数列的前13项之和为 ( )
A.24 B.39 C.52 D.104
5.在实数等比数列![]() 中,有
中,有![]() ( )
( )
A.-8 B.8 C.±8 D.±16
6.![]() ,则a的值等于 ( )
,则a的值等于 ( )
A.3 B.2 C.1.5 D.4
7.已知![]() 的夹角是 ( )
的夹角是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设函数![]() 是定义在R上的奇函数,若
是定义在R上的奇函数,若![]() ,则a的取值范围是
,则a的取值范围是
( )
A.![]() B.
B.![]() 且
且![]() C.
C.![]() 且
且![]() D.-1<
D.-1<![]()
9.若函数![]() 是定义在(0,+
是定义在(0,+![]() )上的增函数,且对一切x>0,y>0满足
)上的增函数,且对一切x>0,y>0满足![]() ,则不等式
,则不等式![]() 的解集为 ( )
的解集为 ( )
A.(-8,2) B.(2,+![]() ) C.(0,2) D.(0,+
) C.(0,2) D.(0,+![]() )
)
|
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.设O是△ABC内部一点,且![]() 的面积之比为( )
的面积之比为( )
A.2 B.![]() C.1 D.
C.1 D.![]()
12.已知函数![]() 的导数
的导数![]() 处取到极大值,则a的取值范围是 ( )
处取到极大值,则a的取值范围是 ( )
A.(-![]() ,-1) B.(-1,0) C.(0,1) D.(0,+
,-1) B.(-1,0) C.(0,1) D.(0,+![]() )
)
|
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
13.已知平面向量![]() 。
。
14.不等式![]() 的解集是
。
的解集是
。
15.已知实数x,y满足不等式组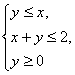 那么目标函数
那么目标函数![]() 的最大值是
。
的最大值是
。
16.在数列中,已知![]() ,这个数列的通项公式是
,这个数列的通项公式是![]() =
。
=
。
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)已知集合![]()
(1)若![]() ,求a的取值范围;
,求a的取值范围;
(2)若![]() ,求a的取值范围。
,求a的取值范围。
18.(本小题满分12分)已知函数![]() 在点x0处取得极小值-5,其导函数
在点x0处取得极小值-5,其导函数![]() 的图象经过点(0,0),(2,0)。
的图象经过点(0,0),(2,0)。
(1)求a,b的值;
(2)求x0及函数![]() 的表达式。
的表达式。
19.(本小题满分12分)已知函数![]() 有两实根
有两实根![]()
(1)求函数![]() 的解析式;
的解析式;
(2)设k>1,解关于x的不等式![]()
20.(本小题满分12分)设函数![]() 对任意x,y
对任意x,y![]() ,都有
,都有![]() ,
,![]() <0;f(1)=-2.
<0;f(1)=-2.
(1)求证![]() 是奇函数;
是奇函数;
(2)试问在![]()
![]() 是否有最值?如果有求出最值;如果没有,说明理由。
是否有最值?如果有求出最值;如果没有,说明理由。
21.(本小题满分14分)已知p>1,设函数![]()
(1)求![]() 的定义域;
的定义域;
(2)![]() 是否存在最大值或最小值?如果存在,请把它求出来;若不存在,请说明理由。
是否存在最大值或最小值?如果存在,请把它求出来;若不存在,请说明理由。
22.(本小题满分14分)已知数列![]() 中,
中,![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]()
(3)设![]() 是否存在最大的整数m,使得对任意
是否存在最大的整数m,使得对任意![]() ,均有
,均有![]() 成立?若存在,求出m,若不存在,请说明理由。
成立?若存在,求出m,若不存在,请说明理由。
高三数学第二次诊断性考试
数学试题(文科)参考答案
|
1—6 CADCB 7—12 ACCCDBB
二、填空题
13.-6; 14.![]() ; 15.4 16.
; 15.4 16.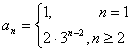
三、解答题
17.(本小题满分10分)
解:![]()
(1)![]()
![]()
a<0时,![]()
a<0时,![]()
a=0时,![]() 显然不符合条件。
显然不符合条件。
![]() ……………………6分
……………………6分
(2)要满足![]() 时成立
时成立
∵此时B![]()
故所求的a值为3。…………………………10分
18.(本小题满分12分)
解:(1)由题设可得![]()
![]() 的图像过点(0,0),(2,0)
的图像过点(0,0),(2,0)
![]()
解之得:![]() ……………………6分
……………………6分
(2)由![]() >0,得x>2,或x<0;
>0,得x>2,或x<0;
![]()
上![]()
![]()
![]() 上递增,
上递增,
在(0,2)上递减,
因此![]() 处取得极小值,所以x0=2
处取得极小值,所以x0=2
由f(2)=-5,得c=-1
![]()
19.(本小题满分12分)
解:(1)将x1=3,x2=4分别代入方程![]() 得
得
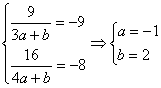
所以![]() ……………………6分
……………………6分
(2)不等式即为![]()
即![]()
①当1<k<2时,解集为![]() ;
;
②当k=2时,解集为![]() ;
;
③当k>2时,解集为![]() ……………………12分
……………………12分
20.(本小题满分12分)
解:(1)证明:令x=y=0,则有f(0)=2f(0)![]() f(0)=0
f(0)=0
令![]() ,则有
,则有![]()
即![]()
![]() 是奇函数…………………………5分
是奇函数…………………………5分
(2)任取![]()
且![]()
![]()
![]() 在R上为减函数。
在R上为减函数。
因此![]() 为函数的最大值。
为函数的最大值。
![]()
![]()
∴函数最大值为6,最小值为-6……………………12分
21.(本小题满分14分)
解:(1)由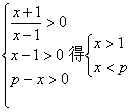
所以![]() 的定义域为(1,p)……………………5分
的定义域为(1,p)……………………5分
(2)![]()
![]() 既无最大值又无最小值;
既无最大值又无最小值;
![]()
![]() 时,
时,
![]() 但没有最小值。
但没有最小值。
p>3,![]() 有最大值
有最大值![]() ,但没有最小值………………14分
,但没有最小值………………14分
综上可知:![]() ,
,![]() 既无最大值也无最小值。
既无最大值也无最小值。
22.(本小题满分14分)
解:(1)![]() ……………………5分
……………………5分
(2)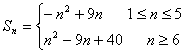 ……………………10分
……………………10分
(3)由(1)可得![]()
则![]()
![]()
![]() ……………………12分
……………………12分
由Tn为关于n的增函数,
故![]() ,于是欲使
,于是欲使![]() 恒成立
恒成立
则![]()
∴存在最大的整数m=7满足题意…………………………14分