高三数学联合调研考试试题
(试卷总分:150分 考试时间:120分钟)
一 .填空题:(本大题10个小题,每小题5分,共50分,把答案填在题中横线上)
1. 已知集合M={xx<3},N={xlog2x<1},则M∩N= ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 在![]() 中,
中,![]() 则
则![]() 形状为(
)
形状为(
)
A . 直角三角形 B. 等腰或直角三角形
C . 正三角形 D . 等腰直角三角形
3. 已知直线a、b和平面![]() ,则
,则![]() 的一个必要不充分条件是( )
的一个必要不充分条件是( )
A. ![]() B.
B.
![]()
C. ![]() D.
D.
![]() 与平面
与平面![]() 成等角
成等角
4.若![]()
![]() 且
且![]() ,则下列不等式正确的是
,则下列不等式正确的是
A.![]() B.
B. ![]()
C. ![]() D.
以上均不正确
D.
以上均不正确
5. 正项等比数列{an}满足:a1·a5=1, ![]() = 3, bn=log3an
,则数列{bn}的前10项的和是
= 3, bn=log3an
,则数列{bn}的前10项的和是
A. 65 B. -65 C. 25 D. -25
6. 函数![]()
![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
7. 某餐厅供应客饭,每位顾客可以在餐厅提供菜肴中任选2荤2素共4个不同的品种。现在餐厅准备了5种不同的荤菜,若要保证每位顾客有200种以上的不同选择,则餐厅至少还要准备不同素菜品种
A.5种 B.7种 C. 9种 D. 10种
8. 已知双曲线![]()
![]() 的右焦点为F,右准线为L,过F作
的右焦点为F,右准线为L,过F作![]() 轴的垂线交双曲线于P、Q两点,且
轴的垂线交双曲线于P、Q两点,且![]() 等于直线PQ与L间的距离的4倍,则双曲线的离心率等于
等于直线PQ与L间的距离的4倍,则双曲线的离心率等于
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
9. 在正三棱柱![]() 中,若AB=2,
中,若AB=2,![]() ,则点A到平面
,则点A到平面![]() 的距离为
的距离为
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
10. 已知![]() 和
和![]() 是定义在
是定义在
![]() {
{![]() 1≤
1≤![]() ≤
≤![]() }上的函数,对任意的
}上的函数,对任意的![]() ,存在常数
,存在常数![]() ,使得
,使得![]() ≥
≥![]() ,
,![]() ≥
≥![]() ,且
,且![]() =
=![]() ,则
,则![]() 在A上的最大值为
在A上的最大值为
A.![]() B.
B.![]() C.5 D.
C.5 D.![]()
二 .填空题:(本大题6个小题,每小题5分,共30分,把答案填在题中横线上)
11. 定义”等积数列”:在一个数列中,如果每一项与它的后一项的积都为同一个常数,那么这个数列叫等积数列,这个常数叫做该数列的公积.已知数列![]() 是公积为2的等积数列,且
是公积为2的等积数列,且![]() 则该数列的前
则该数列的前![]()
![]() .
.
12. ![]() 的解集为
的解集为![]() ,则
,则![]() 的最小值为 .
的最小值为 .
13. 直线![]() 有公共点,但 直线不过圆心,则
有公共点,但 直线不过圆心,则![]() 的取值范围是
.
的取值范围是
.
14. 某县城有三所高中,A学校共有学生4000人,B学校生共有学生2000人,C学校共有学生3000人,现欲抽样分析某次考试的情况,由抽取的 900份试卷进行分析,则从A学校抽取的试卷份数应为 .
15. 当![]() ∈[0,
∈[0,![]() ]时,函数
]时,函数![]() 的最大值为4,则
的最大值为4,则![]()
16. 如果函数![]() 在(0,1)内存在与
在(0,1)内存在与![]() 轴平行的切线,则
轴平行的切线,则
实数![]() 的取值范围是
.
的取值范围是
.
三、解答题(本大题共5题;共70分.解答应写出文字说明、证明过程或推演步骤.)
 17.(本小题满分12分)
17.(本小题满分12分)
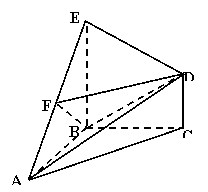
如图,在几何体ABCDE中,△ABC是等腰直角三角形,
∠ABC =900,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.
(1)求证:DF∥平面ABC;
(2)求AB与平面BDF所成角的余弦值的大小.
18.(本小题满分14分)
已知A袋中有4个白球,2个黑球,B袋中有3个白球,4个黑球.
(1)从A袋中任取2个球,求取出的球均为白球的概率;
(2)从A,B两个袋中各取两个球交换放回,求A袋中恰有4个白球的概率.
19. (本小题满分14分)已知函数![]() 在区间[0,1]上单调递增,在区间[1,2]上单调递减.
在区间[0,1]上单调递增,在区间[1,2]上单调递减.
(1)求a的值;
(2)设![]() ,若方程
,若方程![]() 的解集恰有3个元素,求b的取值范围;
的解集恰有3个元素,求b的取值范围;
20. (本小题满分16分)已知数列{an}中,a1>0, 且an+1=![]() ,
,
(1)试求a1的值,使得数列{an}是一个常数数列;
(2)试求a1的取值范围,使得an+1>an对任何自然数n都成立;
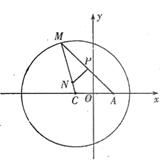
21. (本小题满分14分)如图所示,已知圆![]() 为圆上一动点,点P在AM上,点N在CM上,且满足
为圆上一动点,点P在AM上,点N在CM上,且满足![]() 的轨迹为曲线E.
的轨迹为曲线E.
(1)求曲线E的方程;
(2)过点A且倾斜角是45°的直线l交曲线E于两点H、Q,求HQ.
|
参考答案
1.C 提示: log2x<1=
log22 ![]()
![]() , N={x0<x<2},
, N={x0<x<2},
![]() M∩N={x0<x<2=
M∩N={x0<x<2=
2. 答案:A
提示:![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() 为直角三角形.
为直角三角形.
3. 答案:D.
提示:![]()
![]()
![]() 与平面
与平面![]() 成等角,但是,
成等角,但是,![]() 与平面
与平面![]() 成等角并不一定有
成等角并不一定有
![]() .故
.故![]() 与平面
与平面![]() 成等角是
成等角是![]() 的一个必要不充分条件.
的一个必要不充分条件.
4. 答案:B
提示:![]()
![]() 且
且![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ;
;
![]()
![]() . (
. (![]()
![]()
![]() .
.
5. 答案:D提示:![]() a1·a5=1,
a1·a5=1,![]()
![]()
![]() 公比
公比![]() ,
,
![]() ,
,![]() bn=log3an
=
bn=log3an
=![]() ,
,
![]() {bn}的前10项的和
{bn}的前10项的和![]() -25
-25
6. 答案:A
提示:![]()
![]()
![]() ,
,
![]()
![]()
![]() ,即
,即![]() 时,
时,![]() 有最大值
有最大值![]() .
.
7. 答案:B
提示:设至少还要准备![]() 个不同素菜品种,则每位顾客有
个不同素菜品种,则每位顾客有![]() 种的不同选择,
种的不同选择,
![]()
![]()
![]()
![]() ,即至少还要准备7个不同素菜品种.
,即至少还要准备7个不同素菜品种.
8. 答案:C提示:把![]() 代入
代入![]() 解得
解得 ![]() ,
,![]()
![]()
![]()
![]() ,
,
又![]() PQ与L间的距离为
PQ与L间的距离为 ![]() ,
,![]()
![]() ,
,![]() .
.
 9. 答案:B 提示:如右图,取BC的中点M,做AO
9. 答案:B 提示:如右图,取BC的中点M,做AO![]()
![]() ,易知AO
,易知AO![]() 平面
平面![]() ,
,
线段AO的长度即A到平面![]() 的距离,
的距离,
![]() AO=
AO=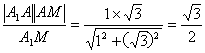
10. 答案:C
提示:![]()
![]() ≥
≥![]() ,
,![]() ≥
≥![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,![]() 在A上的最大值为
在A上的最大值为![]() .
.
12. 答案:3提示:
![]() 的解集为
的解集为![]() ,
,![]()
![]()
13. 答案:![]()
提示:因为有公共点,所以圆心(5,6)到直线![]() 的距离
的距离
![]()
又![]() 直线不过圆心,
直线不过圆心,![]()
![]()
![]() 的取值范围是
的取值范围是![]() .
.
14. 答案:400. 提示:A学校抽取的试卷份数应为![]() 份.
份.
15. 答案:∵ ![]() ,
,![]() ], ∴
], ∴ ![]() .
.
∴ 当![]() 即
即![]() 时,
时,![]() .∵ 3+a=4,∴ a=1.
.∵ 3+a=4,∴ a=1.
16. 答案:![]() 提示:存在与
提示:存在与![]() 轴平行的切线即
轴平行的切线即![]() 有解,
有解,![]() .
.
17. 18.(1)解:取AB的中点G,连CG,FG,
则FG∥BE,且FG=![]() BE,
BE,
∴ FG∥CD且FG=CD, ……3
∴ 四边形FGCD是平行四边形,∴ DF∥CG,
又∵ CG![]() 平面ABC,
平面ABC,
∴ DF∥平面ABC. ………6分
(2)解法一:设A到平面BDF的距离为h,
由 ![]() 得
得 ![]() .
.
在△BDF中,BF=![]() ,BD=DF=
,BD=DF=![]() ,∴
,∴ ![]() =
=![]() ,又
,又![]() =1,
=1,
且CB=2.∴ ![]() .
…..10分
.
…..10分
又设AB与平面BDF所成的角为![]() ,则
,则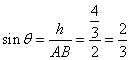 ,
,
故AB与平面BDF所的角的余弦值为![]() .
………12分
.
………12分
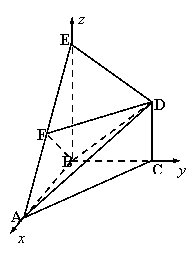 解法二:以点B为原点,BA、BC、BE所在的直线分别为 x、y、z轴,建立如图的空间直角坐标系,则
解法二:以点B为原点,BA、BC、BE所在的直线分别为 x、y、z轴,建立如图的空间直角坐标系,则
B(0,0,0), A(2,0,0), C(0,2,0),
D(0,2,1), E(0,0,2), F(1,0,1).
∴ ![]() =(0,2,1),
=(0,2,1),![]() =(1,-2,0)
=(1,-2,0)
设平面BDF的一个法向量为![]() =(2,a,b),
=(2,a,b),
∵ ![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
∴ 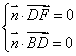 ,
,
即![]() ,解得
,解得![]() ,∴
,∴ ![]() ……..10分
……..10分
又设AB与平面BDF所成的角为![]() ,则法线
,则法线![]() 与
与![]() 所成的角为
所成的角为![]() ,
,
∴ ![]() =
=![]() =
=![]() ,
,
即 ![]() ,故AB与平面BDF所成的角的余弦值为
,故AB与平面BDF所成的角的余弦值为![]() .
…… 12分
.
…… 12分
18.解(1)2球均为白球的概率为![]() ………………..4分(文6分)
………………..4分(文6分)
(2) A袋中恰有4个白球的概率为
![]() ……………..8分(文12分)
……………..8分(文12分)
19. 解(1)![]() , ………………..2分
, ………………..2分
由已知![]() 上的值恒为正,在
上的值恒为正,在![]() 上的值恒为负,
上的值恒为负,
![]()
![]() ……..……6分
……..……6分
(2)由![]()
![]() 有三个相异实根, ………….8分
有三个相异实根, ………….8分
故方程![]() 有两个相异的非零根.
有两个相异的非零根. ![]() …………..12分
…………..12分
21. 解:(1)![]()
∴NP为AM的垂直平分线,∴NA=NM. …………………..2分
又![]()
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.
且椭圆长轴长为![]() 焦距2c=2.
焦距2c=2.
![]() …………5分
…………5分
∴曲线E的方程为![]() ……………..6分
……………..6分
(2)直线![]() 的斜率
的斜率![]() ∴直线
∴直线![]() 的方程为
的方程为 ![]() ………..8分
………..8分
由  …………………..10分
…………………..10分
设![]() ,
,
![]() ……12分
……12分