三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)
| |
|
(Ⅱ)若![]() ,求实数a的取值范围.
,求实数a的取值范围.
16.(本小题满分13分)
已知函数![]()
(Ⅰ)求![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)若不等式![]() 都成立,求实数m的最大值.
都成立,求实数m的最大值.
17.(本小题满分13分)
一盒中放有除颜色不同外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(Ⅰ)从盒中同时摸出两个球,求两球颜色恰好相同的概率;
(Ⅱ)从盒中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
18.(本小题满分13分)
已知等比数列![]() 中,
中,![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)试比较![]() 的大小,并说明理由.
的大小,并说明理由.
19.(本小题满分14分)
已知向量![]() 且满足
且满足![]() ,其中O为坐标原点,K为参数.
,其中O为坐标原点,K为参数.
(Ⅰ)求动点M的轨迹方程,并判断曲线类型;
(Ⅱ)如果动点M的轨迹是一条圆锥曲线,其离心率e满足![]() ,求实数K的取值范围.
,求实数K的取值范围.
15.解:(Ⅰ)因为![]() 所以
所以![]()
![]() ……2分
……2分
|
所以( ![]()
…………………………………………………………………………6分
|
|
|
|
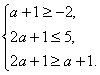
解得![]() ……………………………………………………………9分
……………………………………………………………9分
当![]()
![]() ,即
,即![]() 时
时![]() 此时有P=
此时有P=![]()
![]() ,
,
所以![]() 为所求.
为所求.
综上,实数a的取值范围是![]() …………………………13分
…………………………13分
16.解:(Ⅰ)因为![]()
![]() ……………………2分
……………………2分
![]() ………………………………4分
………………………………4分
由![]()
得![]()
所以![]() 的单调增区间是
的单调增区间是![]() ……………………8分
……………………8分
(Ⅱ)因为![]()
所以![]() …………………………………………9分
…………………………………………9分
所以![]() ………………………………10分
………………………………10分
所以![]() 的最大值为1.……………………………………13分
的最大值为1.……………………………………13分
17.解(Ⅰ)从盒中同时摸出两个球有![]() 种可能情况.……………………2分
种可能情况.……………………2分
摸出两球颜色恰好相同即两个黑球或两个白球,
若有![]() 种可能情况.……………………………………5分
种可能情况.……………………………………5分
故所求概率为![]() ………………………………7分
………………………………7分
(Ⅱ)有放回地摸两次,两球颜色不同,即“先黑后白”或“先白后黑”,
菜有![]() 种可能情况.
种可能情况.
故所求概率为![]() ………………13分
………………13分
18.解:(Ⅰ)设数列![]() 的公比为q,则根据条件得
的公比为q,则根据条件得
|
|
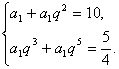 即
即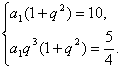 …………………………2分
…………………………2分
②÷①得![]() 代入①解得
代入①解得![]() …………………………5分
…………………………5分
所以![]() ………………………………6分
………………………………6分
(Ⅱ)因为![]() …………………………7分
…………………………7分
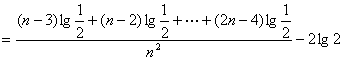
![]()
![]() ………………………………9分
………………………………9分
![]()
![]() ……………………………………………………10分
……………………………………………………10分
设![]()
因为![]() 的减函数,所以
的减函数,所以![]()
即![]()
所以![]() ………………………………13分
………………………………13分
19.解(Ⅰ)设![]()
则由![]() 且O为原点A(2,0),B(2,1),C(0,1).
且O为原点A(2,0),B(2,1),C(0,1).
从而![]()
![]() …………………………………………………………………………2分
…………………………………………………………………………2分
代入![]() 为所求轨迹方程.…………………………………………………………………………3分
为所求轨迹方程.…………………………………………………………………………3分
当K=1时,得![]() 轨迹为一条直线;……………………………………4分
轨迹为一条直线;……………………………………4分
当![]()
若K=0,则为圆;………………………………………………5分
若![]() ,则为双曲线;…………………………………………6分
,则为双曲线;…………………………………………6分
若![]() ,则为椭圆.……………………………………7分
,则为椭圆.……………………………………7分
(Ⅱ)因为![]() ,所以方程表示椭圆.……………………………………9分
,所以方程表示椭圆.……………………………………9分
对于方程![]()
①当![]()
此时![]() ……………………11分
……………………11分
②当![]()
![]()
所以![]() ……………………13分
……………………13分
所以![]() ……………………………………………………14分
……………………………………………………14分