三、解答题:（本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.）
15.（本小题满分13分）
在三角形
中，
、
、
的对边分别为
、
、
，若
（Ⅰ）求的大小
（Ⅱ）若
、
，求三角形的面积.
16．（本小题共13分）
已知圆
方程为：
.
（Ⅰ）直线
过点
，且与圆交于
、
两点，若
，求直线的方程;
（Ⅱ）过圆上一动点
作平行于
轴的直线
，设与
轴的交点为
，若向量
，求动点
的轨迹方程，并说明此轨迹是什么曲线.
17.（本小题满分13分）
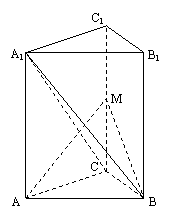如图, 在直三棱柱ABC－A1B1C1中，∠ACB=90°，CB=1,CA=
, AA1=
,M为侧棱CC1上一点, 
.
（I）求证:
AM^平面
；
（II）求二面角B－AM－C的大小;
（Ⅲ）求点C到平面ABM的距离.
19.（本小题满分14分）
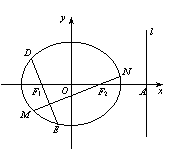设椭圆
的焦点分别为
，右准线交轴于点A，且
.
（Ⅰ）试求椭圆的方程；
（Ⅱ）过
、
分别作互相垂直的两直线与椭圆分别交于D、E、
M、N四点（如图所示），试求四边形DMEN面积的最大值和最小值.
15．本小题满分13分
解（Ⅰ）由已知及正弦定理可得
2分
∴
又在三角形
中，
3分
∴
，即
，
5分
6分
（Ⅱ）∵
∴
8分
又∵
∴
10分
∴
即
13分
16．本小题满分13分
解（Ⅰ）①当直线
垂直于
轴时，则此时直线方程为
，与圆的两个交点坐标为
和
，其距离为
满足题意
1分
②若直线不垂直于轴，设其方程为
，即
2分
设圆心到此直线的距离为
，则
，得
3分
∴
，
，
4分
故所求直线方程为
5分
综上所述，所求直线为或
6分
（Ⅱ）设点
的坐标为
（
），
点坐标为
则
点坐标是
7分
∵
，
∴
即
，
9分
又∵
，∴
11分
∴点的轨迹方程是
，
12分
轨迹是一个焦点在轴上的椭圆，除去短轴端点。
13分
注：多端点时，合计扣1分。
17．本小题满分13分
解：（I）在直三棱柱ABC－A1B1C1中，易知面ACC1A1⊥面ABC，
∵∠ACB=90°，
∴BC⊥面ACC1A1，……………… 2分
∵
面ACC1A1
∴BC⊥AM
∵，且
∴ AM^平面………………4分
（II）设AM与A1C的交点为O，连结BO，由（I）可知AM ^ OB，且AM ^ OC，
所以∠BOC为二面角B－AM－C的平面角， ………………………5分
在RT△ACM和RT△A1AC中，∠OAC+∠ACO=90°，
∴∠AA1C=∠MAC
∴RT△ACM∽RT△A1AC
∴
∴
…………… 7分
∴在RT△ACM中，
∵
∴
∴在RT△BCO中，
∴
，故所求二面角的大小为45°……………… 9分
（Ⅲ）设点C到平面ABM的距离为h，易知
，
可知
…………………10分
∵
…………………11分
∴
∴
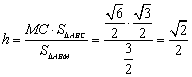
∴点C到平面ABM的距离为
………………13分
19．本小题满分14分
解（Ⅰ）由题意，
， ∴
，
2分
∵ ∴为A的中点
3分
∴
，
即
椭圆方程为
.
5分
（Ⅱ）当直线DE与轴垂直时，
，
此时
，四边形
的面积为
.
同理当MN与轴垂直时，也有四边形的面积为. 7分
当直线DE，MN均与轴不垂直时，设
，代入椭圆方程，消去得：
.
设
，
，则
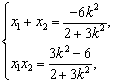8分
所以，
，
所以，
，
同理，
.
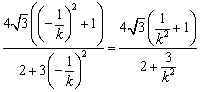10分
所以，四边形的面积
=
=
，
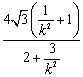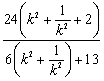令
，得
因为
，
当
时，
，且S是以
为自变量的增函数，
所以
综上可知，四边形DMEN面积的最大值为4，最小值为
.
14分