三、解答题:本大题共6小题,共80分. 解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分12分)已知![]() 、
、![]() 、
、![]() 三点的坐标分别为
三点的坐标分别为![]() (
(![]() ,
,![]() ,
,
![]() (
(![]() ,
,![]() ,
,![]() (
(![]() ,0).
,0).
(Ⅰ)求向量![]() 和向量
和向量![]() 的坐标;
的坐标;
(Ⅱ)设![]() ,求
,求 ![]() 的最小正周期;
的最小正周期;
(Ⅲ)求当![]() ,
,![]() 时,
时,![]() 的最大值及最小值.
的最大值及最小值.
16.(本小题满分13分)
已知函数![]() 是
是![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() 取得极值
取得极值![]() .
.
(Ⅰ)求函数![]() 的解析式; (Ⅱ)求
的解析式; (Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)当![]()
![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
17.(本小题满分13分)
已知数列{![]() }满足
}满足![]() ,且
,且![]() .
.
(Ⅰ)求![]() ,
,![]() ;(Ⅱ)证明数列{
;(Ⅱ)证明数列{![]() }是等差数列;(Ⅲ)求数列{
}是等差数列;(Ⅲ)求数列{![]() }的前
}的前![]() 项之和
项之和![]() .
.
18.(本小题满分14分)
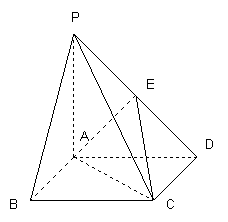
如图,在四棱锥![]() 中,四边形
中,四边形![]() 为正方形,
为正方形,![]() 点在平面
点在平面![]() 内的射影为
内的射影为![]() ,且
,且![]() ,
,![]() 为
为![]() 中点.
中点.
 (Ⅰ)证明:
(Ⅰ)证明:![]() //平面
//平面![]() ;
;
(Ⅱ)证明:平面![]() 平面
平面![]() ;
;
(Ⅲ)求二面角![]() 的大小.
的大小.
15.(本小题满分12分)
解:(Ⅰ)![]() =
=![]() ,
,![]() ,
,
![]() =
=![]() ,
,![]() .
…………………………………2分
.
…………………………………2分
(Ⅱ)![]()
![]()
= ![]() …………4分
…………4分
= ![]()
= ![]() …………………………………6分
…………………………………6分
= ![]()
=![]() …………………………………8分
…………………………………8分
∴![]() 的最小正周期
的最小正周期![]() .
…………………………………9分
.
…………………………………9分
(Ⅲ)∵ ![]()
![]() , ∴
, ∴![]() .
.
∴ 当![]() ,即
,即![]() =
=![]() 时,
时,![]() 有最小值
有最小值![]() , ………………11分
, ………………11分
当![]() ,即
,即![]() =
=![]() 时,
时,![]() 有最大值
有最大值![]() . ……………12分
. ……………12分
16.(本小题满分13分)
解:(Ⅰ)由![]() 是R上的奇函数,有
是R上的奇函数,有![]() ,
…………………………1分
,
…………………………1分
即![]() ,所以
,所以![]() .
.
因此![]() .
…………………………………2分
.
…………………………………2分
对函数![]() 求导数,得
求导数,得![]() . ……………………………3分
. ……………………………3分
由题意得![]() ,
,![]() , ……………………………4分
, ……………………………4分
所以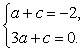 …………………………………5分
…………………………………5分
解得![]() ,
,
因此![]() . …………………………………6分
. …………………………………6分
(Ⅱ)![]()
![]() .
………………………7分
.
………………………7分
令![]() >0,解得
>0,解得![]() <
<![]() 或
或![]() >
>![]() ,
,
因此,当![]() (-∞,-1)时,
(-∞,-1)时,![]() 是增函数;
是增函数;
当![]() (1,+∞)时,
(1,+∞)时,![]() 也是增函数. …………………………………8分
也是增函数. …………………………………8分
再令![]() <0,
解得
<0,
解得![]() <
<![]() <
<![]() ,
,
因此,当![]() (-1,1)时,
(-1,1)时,![]() 是减函数. ……………………………9分
是减函数. ……………………………9分
(Ⅲ)令![]() =0,得
=0,得![]() =-1或
=-1或![]() =1.
=1.
当![]() 变化时,
变化时,![]() 、
、![]() 的变化如下表.
的变化如下表.
|
|
|
| -1 |
| 1 |
| 3 |
|
|
| + | 0 | - | 0 | + |
|
|
|
| ↗ |
| ↘ |
| ↗ | 18 |
…………………………………11分
从上表可知,![]() 在区间
在区间![]() 上的最大值是18 .
上的最大值是18 .
原命题等价于m大于![]() 在
在![]() 上的最大值,
上的最大值,
∴![]() . …………………………………13分
. …………………………………13分
17.(本小题满分13分)
解:(Ⅰ)![]() ,
,
![]() .
…………………………………2分
.
…………………………………2分
(Ⅱ)![]() ,
,
∴![]() , …………………………………3分
, …………………………………3分
即![]() . …………………………………4分
. …………………………………4分
∴数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列. …………5分
的等差数列. …………5分
(Ⅲ)由(Ⅱ)得
![]() ……………………………7分
……………………………7分
∴![]() .
……………………………8分
.
……………………………8分
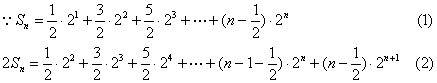
……………………………10分
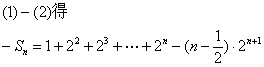
![]()
![]()
![]() .
.
∴![]() .
……………………………13分
.
……………………………13分
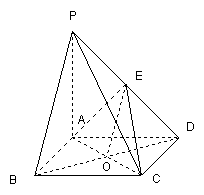 18.(本小题满分14分)
18.(本小题满分14分)
(Ⅰ)
证明:连结BD交AC于点O,连结EO.
![]() O为BD中点,E为PD中点,
O为BD中点,E为PD中点,
∴EO//PB. ……………………1分
![]() EO
EO![]() 平面AEC,PB
平面AEC,PB![]() 平面AEC,
……………………2分
平面AEC,
……………………2分
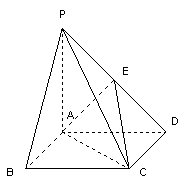 ∴ PB//平面AEC.
……………………3分
∴ PB//平面AEC.
……………………3分
(Ⅱ)
证明:![]() P点在平面ABCD内的射影为A,
P点在平面ABCD内的射影为A,
∴PA⊥平面ABCD.
![]()
![]() 平面ABCD,
平面ABCD,
∴![]() .
……………………4分
.
……………………4分
又![]() 在正方形ABCD中
在正方形ABCD中![]() 且
且![]() , ……………………5分
, ……………………5分
∴CD![]() 平面PAD.
……………………6分
平面PAD.
……………………6分
又![]()
![]() 平面PCD,
平面PCD,
∴平面![]() 平面
平面![]() .
……………………7分
.
……………………7分
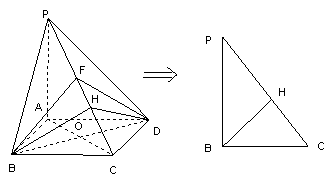 (Ⅲ)
(Ⅲ)
解法一:过点B作BH![]() PC于H,连结DH.
……………………8分
PC于H,连结DH.
……………………8分
易证![]() ,
,![]() DH
DH![]() PC,BH=DH,
PC,BH=DH,
∴![]() 为二面角B—PC—D的平面角.
……………………10分
为二面角B—PC—D的平面角.
……………………10分
![]() PA⊥平面ABCD,
PA⊥平面ABCD,
∴AB为斜线PB在平面ABCD内的射影,
又BC⊥AB,
∴BC⊥PB.
又BH![]() PC,
PC,
∴![]() ,
,
![]() ,
……………………11分
,
……………………11分
在![]() 中,
中,
![]()
=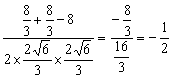 , ……………………12分
, ……………………12分
∴ ![]() ,
……………………13分
,
……………………13分
∴二面角B—PC—D的大小为![]() .
……………………14分
.
……………………14分