三、解答题：本大题共6小题，共80分. 解答应写出文字说明，证明过程或演算步骤.
15．（本小题满分12分）
已知{
}是等差数列，
（I）求{}的通项公式；
（II）设{}的前n项和
，求n的值.
16．（本小题13分）
已知函数
（I）求
的定义域；
（II）求的值域；
（III）设α的锐角，且
的值.
17．（本小题13分）
在一天内甲、乙、丙三台设备是否需要维护相互之间没有影响，且甲、乙、丙在一天内不需要维护的概率依次为0.9、0.8、0.85. 则在一天内
（I）三台设备都需要维护的概率是多少？
（II）恰有一台设备需要维护的概率是多少？
（III）至少有一台设备需要维护的概率是多少？
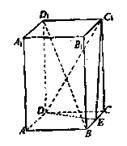
18．（本小题13分）
|
（I）求异面直线AA1和BD1所成角的大小；
（II）求证：BD1∥平面C1DE；
（III）求二面角C1—DE—C的大小.
19．（本小题满分13分）
设
函数
（I）求的反函数
；
（II）若在[0，1]上的最大值与最小值互为相反数，求a的值；
（III）若的图象不经过第二象限，求a的取值范围.
三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.
15．（本小题满分12分）
（Ⅰ）解：
设等差数列
则
……………………2分
解得
…………………………4分
所以数列
的通项为
……………………6分
（Ⅱ）解：
数列的前n项和
…………………………9分
由
即
所以
……………………………………12分
16．（本小题满分12分）
（I）解：由
…………………………………………………………1分
得
，……………………………………………………3分
所以的定义域为
.……………………………4分
（III）解：因为α是锐角，且
，从而
，…………5分
，………………………………………………………………8分
…………………………………………………………11分
故
.………………………………………………12分
17．（本小题满分13分）
解：记甲、乙、丙三台设备在一天内不需要维护的事件分别为A，B，C，
则
（I）解：三台设备都需要维护的概率
……………………………………2分
=（1－0.9）×（1－0.8）×（1－0.85）=0.003.
答：三台设备都需要维护的概率为0.003.…………………………………4分
（II）解：恰有一台设备需要维护的概率
=（1－0.9）×0.8×0.85+0.9×(1－0.8)×0.85+0.9×0.8×(1－0.85)
=0.329.
答：恰有一台设备需要维护的概率为0.329.…………………………8分
（III）解：三台设备都不需要维护的概率
，………………11分
所以至少有一台设备需要维护的概率
答：至少有一台设备需要维护的概率为0.388.……………………13分
18．（本小题满分14分）
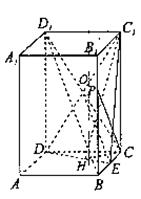
（I）解：连接B1D1.∵在正四棱柱ABCD—A1B1C1D1中，AA1//BB1，
是异面直线
所成的角.……………………2分
即在侧棱BB1上不存在点P，使得CP⊥平面C1DE.………………………14分
在
，
即异面直线所成角的大小为
……………………4分
|
∵CDD1C1是矩形，∴O是CD1的中点，
又E是BC的中点，∴EO∥BD1.………………2分
又BD1
平面C1DE，EO
平面C1DE，
∴BD1∥平面C1DE.……………………………4分
（III）解：过点C作CH⊥DE于H，连接C1H.
在正四棱柱ABCD—A1B1C1D1中，CC1⊥平面ABCD，
∴C1H⊥DE，∠C1HC是二面角C1—DE—C的平面角.……………………………………11分
在
在
…………………………13分
∴二面角C1—DE—C的大小为
…………………………14分
19．（本小题满分14分）
（Ⅰ）解：因为
所以的值域是
…………………………2分
设
所以的反函数为
……4分
（Ⅱ）解：当
时，
函数
为
上的增函数，………………6分
所以
即
解得
……………………………………8分
（Ⅲ）解：当时，函数是上的增函数，且经过定点（－1，－1）.
所以的图象不经过第二象限的充要条件是的图象与x轴的交点位于x轴的非负半轴上. ……………………………………11分
令
解得
由
………………………………14分