三．解答题：本大题共6小题，满分75分。解答应写出文字说明，证明过程或演算步骤。
1.(本大题满分12分)设
，已知
，
，其中
．(1)若
，且a = 2b，求
的值；
(2)若
，求
的值．
|
|
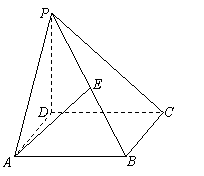
2.(本大题满分12分)如图，在四棱锥P－ABCD中，底面ABCD为正方形，PD⊥平面ABCD，且PD = AB
= a，E是PB的中点，F为AD中点．
(1)求异面直线PD、AE所成的角；
(2)求证：EF⊥平面PBC．
(3)求二面角F－PC－E的大小．
3.(本大题满分12分)已知10件产品中有3件是次品．
(1)任意取出3件产品作检验，求其中至少有1件是次品的概率；
(2)为了保证使3件次品全部检验出的概率超过0.6，最少应抽取几件产品作检验？
4.(本大题满分12分)在平面直角坐标系中，已知点A(1，0)，向量e = (0，1)，点B为直线
上的动点，点C满足
，点M满足
，
．
(1)试求动点M的轨迹E的方程；
(2)试证直线CM为轨迹E的切线．
三．解答题：
16．(1)解：∵，∴a =
(1，
)，b =
(
，
) 2分
由a = 2b，得
，∴
(k ÎZ) 6分
(2)解：∵a·b =
2cos2
=
8分
∴
，即 
10分
整理得
，∵，∴
． 12分
17．(1)解：连AC、BD交于H，连结EH，则EH∥PD，
∴∠AEH异面直线PD、AE所成的角 2分
∵
，
∴
，即异面直线AE、DP所成角为
． 4分
(2)解：F为AD中点．
连EF、HF，∵H、F分别为BD、AD中点，∴HF∥AB，故HF⊥BC
又EH⊥BC，∴BC⊥平面EFH，因此BC⊥EF 6分
又
，
E为PB中点，∴EF⊥PB，∴EF⊥平面PBC． 8分
(3)解：∵PD⊥平面ABCD，∴CD是PC在平面ABCD上的射影．
又∵CD⊥BC，由三垂线定理，有PC⊥BC．
取PC的中点G，连结EG，则EG∥BC，∴EG⊥PC
连结FG，∵EF⊥平面PBC，∴EG是FG在平面PBC上的射影，且PC⊥EG，
∴FG⊥PC，∴∠FGE为二面角F－PC－E的平面角 10分
∵
，
∴
，∴二面角F－PC－E的大小为． 12分
18．(1)解：任意取出3件产品作检验，全部是正品的概率为
3分
至少有一件是次品的概率为
6分
(2)设抽取n件产品作检验，则3件次品全部检验出的概率为
8分
由
得：
整理得：
， 10分
∵n∈N*，n≤10，∴当n = 9或n = 10时上式成立
∴任意取出3件产品作检验，其中至少有1件是次品的概率为
；为了保证使3件次品全部检验出的概率超过0.6，最少应抽取9件产品作检验 12分
19．(1)解：设B (
，m)，C(x1，y1)），
由，得：2(x1，y1) = (1，0) + (－1，m)，解得x1 = 0，
2分
设M(x，y)，由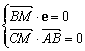
，得
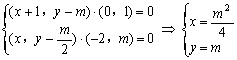， 4分
消去m得E的轨迹方程
． 6分
(2)解：由题设知C为AB中点，MC⊥AB，故MC为AB的中垂线，MB∥x轴，
设M(
)，则B(－1，y0)，C(0，
)，
当y0≠0时，
，MC的方程
8分
将MC方程与联立消x，整理得：
，
它有唯一解
，即MC与只有一个公共点，
又
，所以MC为的切线． 10分
当y0 = 0时，显然MC方程x = 0为轨迹E的切线
综上知，MC为轨迹E的切线．