高三数学八校联考测试试题
一、填空题(4′×12):
1、不等式![]() 的解集是
的解集是 ![]() 。
。
2、(理)设![]() 、
、![]() 是方程
是方程![]() 的两根,则
的两根,则![]()
![]() 。
。
(文)设![]() 、
、![]() 是方程
是方程![]() 的两根,则
的两根,则![]()
![]() 。
。
3、数列![]() 中的第2010项是
中的第2010项是 ![]() 。
。
4、集合![]() 非空,则
非空,则![]() 中所有元素的和是
中所有元素的和是 ![]() 。
。
5、若![]() ,则复数
,则复数![]() 的模是
的模是 ![]() 。
。
6、已知函数![]() 的反函数是
的反函数是![]() ,则方程
,则方程![]() 的解是
的解是 ![]() 。
。
7、已知数列![]() 是公差不为零的等差数列,设
是公差不为零的等差数列,设![]() ,则数列
,则数列![]() 的前
的前![]() 项和
项和![]() 的表达式可以
的表达式可以
是 ![]() 。(用
。(用![]() 中的项表示)
中的项表示)
8、关于函数![]() 有下列命题:①
有下列命题:①![]() 的定义域是
的定义域是![]() ;②
;②![]() 是偶函数;③
是偶函数;③![]() 在定义域内是增函数;④
在定义域内是增函数;④![]() 的最大值是
的最大值是![]() ,最小值是
,最小值是![]() 。其中正确的命题是 ②④ 。(写出你所认为正确的所有命题序号)
。其中正确的命题是 ②④ 。(写出你所认为正确的所有命题序号)
9、走廊上有一排照明灯共![]() 盏,为了节约用电,要关掉其中的三盏。如果关掉的三盏灯不是两端的灯,且任意两盏都不相邻,就不会影响照明,那么随机关掉其中的三盏灯,影响照明的概率是
盏,为了节约用电,要关掉其中的三盏。如果关掉的三盏灯不是两端的灯,且任意两盏都不相邻,就不会影响照明,那么随机关掉其中的三盏灯,影响照明的概率是
![]() 。
。 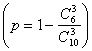
10、(理)设函数![]() 的图像与直线
的图像与直线![]() 及
及![]() 轴所围成图形的面积称为函数
轴所围成图形的面积称为函数![]() 在
在![]() 上的面积。已知函数
上的面积。已知函数![]() 在
在![]() 上的面积为
上的面积为![]() ,则函数
,则函数![]() 在
在![]() 上的面积为
上的面积为 ![]() 。
。
(文)设函数![]() 的图像与直线
的图像与直线![]() 及
及![]() 轴所围成图形的面积称为函数
轴所围成图形的面积称为函数![]() 在
在![]() 上的面积。已知函数
上的面积。已知函数![]() 在
在![]() 上的面积为
上的面积为![]() ,则函数
,则函数![]() 在
在![]() 上的面积为
上的面积为 ![]() 。
。
11、用锤子以均匀的力敲击铁钉入木板。随着铁钉的深入,铁钉所受的阻力会越来越大,使得每次钉入木板的钉子长度后一次为前一次的![]() 。已知一个铁钉受击
。已知一个铁钉受击![]() 次后全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的
次后全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的![]() ,请从这个实事中提炼出一个不等式组是
,请从这个实事中提炼出一个不等式组是 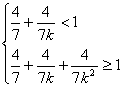 。
。
12、(理)已知![]() ,记
,记![]() ,(其中
,(其中![]() ),例如:
),例如:![]()
![]() 。设
。设![]() ,且满足
,且满足![]() ,则有序数组
,则有序数组![]()
是 ![]() 。
。 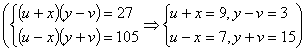
(文)在![]() 中,
中,![]() 的面积为
的面积为![]() ,则
,则![]() 的值为
的值为 ![]() 。
。
二、选择题(4′×4):
13、设![]() 、
、![]() 是两个集合,对于
是两个集合,对于![]() ,下列说法正确的是
( D
)
,下列说法正确的是
( D
)
A.存在![]() ,使
,使![]() B.
B.![]() 一定不成立 C.
一定不成立 C.![]() 不可能为空集 D.
不可能为空集 D.![]() 是
是![]() 的充分条件
的充分条件
14、(理)若![]() ,则
,则![]() 一定不属于的区间是
( C )
一定不属于的区间是
( C )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
(文)若![]() ,则
,则![]() 一定不属于的区间是
( D )
一定不属于的区间是
( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
15、(理)满足不等式![]() 的正整数
的正整数![]() 的个数记为
的个数记为![]() ,
,![]() 的前
的前![]() 项和记
项和记
为![]() ,则
,则![]()
![]() ( A
)
( A
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文)已知等比数列![]() 的公比是不为
的公比是不为![]() 的正数,数列
的正数,数列![]() 满足
满足![]() ,当
,当![]() ,
,
![]() 时,数列
时,数列![]() 的前
的前![]() 项和最大,则
项和最大,则![]() 的值为
( C
)
的值为
( C
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
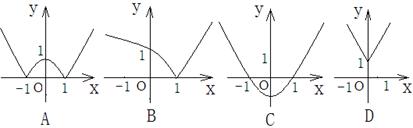 16、已知函数
16、已知函数![]() ,则函数
,则函数![]() 的图像可能是
(
A )
的图像可能是
(
A )
二、解答题(本大题满分86分,共6题):
17、(12′=9′+3′)(理)设![]() 表示幂函数
表示幂函数![]() 在
在![]() 上是增函数的
上是增函数的![]() 的集合;
的集合;![]() 表示不等式
表示不等式
![]() 对任意
对任意![]() 恒成立的
恒成立的![]() 的集合。(1)求
的集合。(1)求![]() ;(2)试写出一个解集为
;(2)试写出一个解集为![]() 的不等式。
的不等式。
(文)设![]() 表示幂函数
表示幂函数![]() 在
在![]() 上是增函数的
上是增函数的![]() 的集合;
的集合;![]() 表示不等式
表示不等式![]() 对任
对任
意![]() 恒成立的
恒成立的![]() 的集合。(1)求
的集合。(1)求![]() ;(2)试写出一个解集为
;(2)试写出一个解集为![]() 的不等式。
的不等式。
解:(理)(1)∵幂函数![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() ,即
,即![]() ,
,
又不等式![]() 对任意
对任意![]() 恒成立,∴
恒成立,∴![]() ,即
,即![]() ,
,
![]() ∴
∴![]() 。
。
(2)一个解集为![]() 的不等式可以是
的不等式可以是 ![]() 。
。
(文)(1)∵幂函数![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() ,即
,即![]() ,
,
又不等式![]() 对任意
对任意![]() 恒成立,∴
恒成立,∴![]() ,即
,即![]() ,
,
∴![]() 。
。
(2)一个解集为![]() 的不等式可以是
的不等式可以是 ![]() 。
。
18、(12′=6′+6′)已知复数![]() ,
,
(1)当![]() 时,求
时,求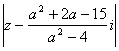 的取值范围;
的取值范围;
(2)(理)是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由。
的值;若不存在,说明理由。
(文)是否存在实数![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由。
的值;若不存在,说明理由。
解:(1)∵![]() ,∴
,∴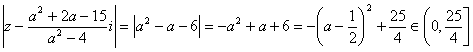 。
。
(2)(理)∵![]() ,∴
,∴![]() 为纯虚数,∴
为纯虚数,∴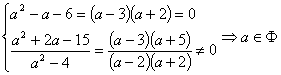
(文)∵![]() ,∴
,∴![]() ,∴
,∴![]() (舍去)
(舍去)![]() 。
。
19、(14′=9′+5′)已知![]() ,关于
,关于![]() 的一元二次方程
的一元二次方程![]() 的两实数根
的两实数根![]() 、
、![]() 满足
满足
![]()
![]()
![]() ,且
,且![]() ,
,
(1)求数列![]() 和
和![]() 的通项公式;(2)求
的通项公式;(2)求![]() 的值。
的值。
解:(1)∵![]()
![]()
![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() 是一个以
是一个以![]() 为首项,
为首项,![]() 为公差的等差数列。∴
为公差的等差数列。∴![]() ,
,
∴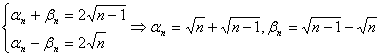 。
。
 (2)
(2)![]()
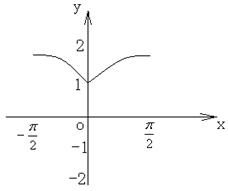
![]() 。20、(16′=4′+12′)已知函数
。20、(16′=4′+12′)已知函数![]() ,
,
(1)在右侧坐标系中作出函数的草图;
(2)研究其值域、奇偶性和单调性,并分别加以证明。
解:(1)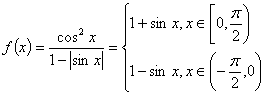 ,
,
(2)![]() 的值域为
的值域为![]() 。
。
∵![]() ,∴
,∴![]() 是偶函数。
是偶函数。
任取![]() ,则
,则![]() ,即
,即![]() ,∴
,∴![]() 在
在![]() 上是增函数,
上是增函数,
又![]() 是偶函数,∴
是偶函数,∴![]() 在
在![]() 上是减函数。
上是减函数。
21、(14′=8′+6′)为了能更好地了解鲸的生活习性,某动物研究所在受伤的鲸身上安装了电子监测装置。从海岸放归点![]() 处(如图所示)把它放归大海,并沿海岸线由西向东不停地对鲸进行了
处(如图所示)把它放归大海,并沿海岸线由西向东不停地对鲸进行了![]() 分钟的跟踪观测,每隔
分钟的跟踪观测,每隔![]() 分钟踩点测得数据如下表(设鲸沿海面游动)。然后又在观测站
分钟踩点测得数据如下表(设鲸沿海面游动)。然后又在观测站![]() 处对鲸进行生活习性的详细观测。已知
处对鲸进行生活习性的详细观测。已知![]() ,观测站
,观测站![]() 的观测半径为
的观测半径为![]() 。
。
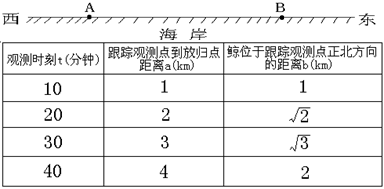 |
(Ⅰ)根据表中数据:①计算鲸沿海岸线方向运动的速度,②写出![]() 、
、![]() 满足的关系式并画出鲸的运动路线简图;
满足的关系式并画出鲸的运动路线简图;
(Ⅱ)若鲸继续以(Ⅰ)中②的运动路线运动,则鲸大约经过多少分钟(从放归时计时),可进入前方观测站![]() 的观测范围(精确到
的观测范围(精确到![]() 分钟)?
分钟)?
解:(Ⅰ)由表中数据知:①鲸沿海岸线方向运行的速度为![]() (km/分钟),②
(km/分钟),②![]() 、
、![]() 满足的关系式为
满足的关系式为![]() ,
,
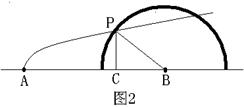
鲸的运动路线图如图![]() :
:
 | |||
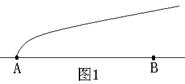 | |||
(Ⅱ)如图![]() ,设鲸所在的位置为点
,设鲸所在的位置为点![]() ,点
,点![]() 位于点
位于点![]() 的正北方向
的正北方向![]() ,点
,点![]() 位于点
位于点![]() 的正东方向
的正东方向![]()
由(Ⅰ)知![]() 。
。
又![]() ,依题意,当鲸到观测站
,依题意,当鲸到观测站![]() 的距离不大于
的距离不大于![]() 时进入观测站
时进入观测站![]() 的观测范围,∴
的观测范围,∴![]() ,∴
,∴![]() ,即
,即 ![]() , ∴
, ∴![]() 。
。
故鲸从A点进入前方观测站B所用的时间大约为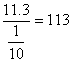 (分钟)。
(分钟)。
答:鲸大约经过113分钟进入B站的观测范围。
22、(18′=4′+8′+6′)(理)已知![]()
![]() 为正常数。
为正常数。
(1)可以证明:定理“若![]() 、
、![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
(2)若![]() 在
在![]() 上恒成立,且函数
上恒成立,且函数![]() 的最大值大于
的最大值大于![]() ,求实数
,求实数![]() 的取值范围,并由此猜测
的取值范围,并由此猜测![]() 的单调性(无需证明);
的单调性(无需证明);
(3)对满足(2)的条件的一个常数![]() ,设
,设![]() 时,
时,![]() 取得最大值。试构造一个定义在
取得最大值。试构造一个定义在
![]() 上的函数
上的函数![]() ,使当
,使当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以![]() 为首项的等差数列。
为首项的等差数列。
解:(1)若![]() 、
、![]() 、
、![]() ,则
,则![]() (当且仅当
(当且仅当![]() 时取等号)。
时取等号)。
(2)![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
又∵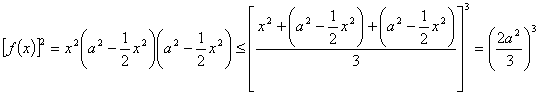
∴![]() ,即
,即![]() 时,
时,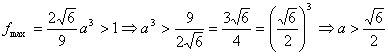 ,
,
又∵![]()
![]() ,∴
,∴![]() 。
综上,得
。
综上,得![]() 。
。
易知,![]() 是奇函数,∵
是奇函数,∵![]() 时,函数有最大值,∴
时,函数有最大值,∴![]() 时,函数有最小值。
时,函数有最小值。
故猜测: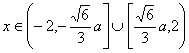 时,
时,![]() 单调递减;
单调递减;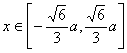 时,
时,![]() 单调递增。
单调递增。
(3)依题意,只需构造以![]() 为周期的周期函数即可。
为周期的周期函数即可。
如对![]() ,
,![]() ,此时
,此时![]() ,
,
即 ![]() 。
。
(文)已知函数![]() ,
,![]() ,
,![]()
(Ⅰ)当![]() 时,若
时,若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对![]() :当
:当![]() 是整数时,存在
是整数时,存在![]() ,使得
,使得![]() 是
是![]() 的最大值,
的最大值,![]() 是
是![]() 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对![]() ,试构造一个定义在
,试构造一个定义在![]() ,且
,且![]() 上的函数
上的函数![]() ,使当
,使当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以![]() 为首项的等差数列。
为首项的等差数列。
解:(Ⅰ)当![]() 时,
时,![]() ,
,
若![]() ,
,![]() ,则
,则![]() 在
在![]() 上单调递减,不符题意。
上单调递减,不符题意。
故![]() ,要使
,要使![]() 在
在![]() 上单调递增,必须满足
上单调递增,必须满足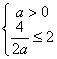 ,∴
,∴![]() 。
。
(Ⅱ)若![]() ,
,![]() ,则
,则![]() 无最大值,故
无最大值,故![]() ,∴
,∴![]() 为二次函数,
为二次函数,
要使![]() 有最大值,必须满足
有最大值,必须满足![]() ,即
,即![]() 且
且![]() ,
,
此时,![]() 时,
时,![]() 有最大值。
有最大值。
又![]() 取最小值时,
取最小值时,![]() ,依题意,有
,依题意,有![]() ,则
,则![]() ,
,
∵![]() 且
且![]() ,∴
,∴![]() ,得
,得![]() ,此时
,此时![]() 或
或![]() 。
。
∴满足条件的实数对![]() 是
是![]() 。
。
(Ⅲ)当实数对![]() 是
是![]() 时,
时,![]()
依题意,只需构造以2(或2的正整数倍)为周期的周期函数即可。
如对![]() ,
,![]() ,
,
此时,![]() ,
,
故![]() 。
。