高三数学复习参考题(35题)
一、选择题
1. (命题人:启东中学)
函数f(x)=x2-a 在区间[-1,1]上的最大值M(a)的最小值是
A.![]() B.
B.![]() C.1
D.2
C.1
D.2
【解析】选B.f(x)是偶函数,所以M(a)是在[0,1]内的最大值,当a≤0时,f(x)=x2-a,则M(a)=1-a;当a>0时,由图像可知,若![]() ,则M(a)=a,若
,则M(a)=a,若![]() ,则M(a)=f(1)=1-a,
,则M(a)=f(1)=1-a,
从而M(a)= 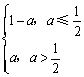 , M(a)min=
, M(a)min=![]() .
.
2. (命题人:海门中学吴健,审题人:沈永飞)
在网络游戏《变形》中,主人公每过一关都以![]() 的概率变形(即从“大象”变为“老鼠”或从“老鼠”变为“大象”),若将主人公过n关不变形的概率计为Pn,则
的概率变形(即从“大象”变为“老鼠”或从“老鼠”变为“大象”),若将主人公过n关不变形的概率计为Pn,则
A.P5>P4 B.P8<P7 C.P11<P12 D.P15>P16
【解析】由题![]() (
(![]() ,
,
即![]() (
(![]() ,以n+1代n,得
,以n+1代n,得![]() ,
,
所以![]() (
(![]() .
.
而![]() ,所以
,所以![]() (
(![]() ).
).
所以![]() 所以偶数项比它相邻项大,所以答案为C.
所以偶数项比它相邻项大,所以答案为C.
3. (命题人:海门市悦来中学何振华,审题人:沈康生)
在矩形ABCD中,AB=3,AD=4,P在AD和DC上运动,设![]() ,将
,将![]() 沿BP折起,使得二面角
沿BP折起,使得二面角![]() 成直二面角,当
成直二面角,当![]() 为( )时,AC长最小.
为( )时,AC长最小.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
 【解析】过A作AH
【解析】过A作AH![]() BP于H,连CH,∴
BP于H,连CH,∴![]() .
.
![]()
![]() ∴
∴![]() .
.
在![]() ,
,
∴在![]() ,
,![]() ,∴
,∴![]() 时,AC长最小;选B.
时,AC长最小;选B.
4. (命题人:通州中学陈颖,审题人:严东来)
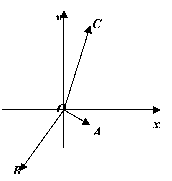
如图,非零向量![]() 与
与![]() 轴正半轴的夹角分
轴正半轴的夹角分
别为 ![]() 和
和![]() ,且
,且![]() ,则
,则
![]() 与
与![]() 轴正半轴的夹角的取值范围是
轴正半轴的夹角的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【解析】![]() 与
与![]() 轴正半轴的夹角的取值范围应在向量
轴正半轴的夹角的取值范围应在向量
![]() 与
与![]() 轴正半轴的夹角之间,故选B.
轴正半轴的夹角之间,故选B.
5. (命题人:通州中学严东来,审题人:王淦华)
已知函数![]() 的定义域是
的定义域是![]() ,值域是
,值域是![]() ,则满足条件的整数对
,则满足条件的整数对![]() 共有
共有
A.2个 B.5个 C.6个 D.无数个
【解析】![]() 在R上是偶函数,故
在R上是偶函数,故![]() 的图象关于y轴对称,作出
的图象关于y轴对称,作出![]() 的图象,截取值域是
的图象,截取值域是![]() 的一段,发现a,b的取值只可能在-2,-1,0,1,2中取得,但必须取0,-2﹑2必须至少取一个,故选B.
的一段,发现a,b的取值只可能在-2,-1,0,1,2中取得,但必须取0,-2﹑2必须至少取一个,故选B.
6. (命题人:平潮高级中学吴杰,审题人:宋军)
三角形ABC中AP为BC边上的中线,![]() ,
,![]() ,则
,则![]() =
=
A.2 B.3 C.![]() D.
D.![]()
【解析】![]() ,即
,即![]() ,
,![]() ,
,
![]()
![]() ,故选C.
,故选C.
7. (命题人:如皋中学薛钧,审题人:冒红玉)
已知双曲线![]() 的左右两焦点分别为
的左右两焦点分别为![]() ,
,![]() 是双曲线右支上的一点,
是双曲线右支上的一点,![]() 点满足
点满足![]() ,
,![]() 在
在![]() 上的投影的大小恰为
上的投影的大小恰为![]() ,且它们的夹角为
,且它们的夹角为![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【解析】因为![]() ,所以
,所以![]() 是一对同向向量,且
是一对同向向量,且![]() .
.
又因为![]() 在
在![]() 上的投影的大小恰为
上的投影的大小恰为![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() 又
又![]() ,
,
所以![]() ,所以
,所以![]()
![]() ,故选A.
,故选A.
8. (命题人:如皋一中潘佩,审题人:戴圩章)
如图1,设P、Q为△ABC内的两点,且![]() ,
,![]() =
=![]()
![]() +
+![]()
![]() ,则△ABP的面积与△ABQ的面积之比为
,则△ABP的面积与△ABQ的面积之比为
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
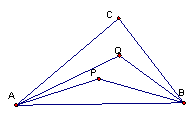
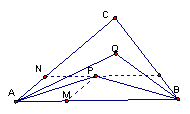
图1 图2
【解析】如图2,设![]() ,
,![]() ,则
,则![]() .由平行四边形法则,知NP∥AB,所以
.由平行四边形法则,知NP∥AB,所以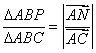 =
=![]() ,同理可得
,同理可得![]() .故
.故![]() ,选B.
,选B.
9. (命题人:海安中学王光华,审题人:王光华)
现准备将![]() 台型号相同的电脑分配给
台型号相同的电脑分配给![]() 所小学,其中
所小学,其中![]() 、
、![]() 两所希望小学每个学校至少
两所希望小学每个学校至少![]() 台,其他小学允许
台,其他小学允许![]() 台也没有,则不同的分配方案共有
台也没有,则不同的分配方案共有
A.![]() 种
B.
种
B.![]() 种
C.
种
C.![]() 种
D.
种
D.![]() 种
种
【解析】法一:分类,“42000型”,共有2种方案;“33000型”,共有1种方案;“32100型”,共有种![]() 种方案;“22200型”,共有3种方案;“22110型”,共有3种方案;故共有15种不同的分配方案.选B.
种方案;“22200型”,共有3种方案;“22110型”,共有3种方案;故共有15种不同的分配方案.选B.
10.(命题人:南通市小海中学夏志辉,审题人:夏志辉)
已知f (x)=x+1,g (x)=2x+1,数列{an}满足:a1=1,an+1=则数列{an}的前2007项的和为
A.5×22008-2008 B.3×22007-5020 C.6×22006-5020 D.6×21003-5020
【解析】∵a2n+2=a2n+1+1=(2a2n+1)+1=2a2n+2,∴a2n+2+2==2(a2n+2),
∴数列{a2n+2}是以2为公比、以a2=a1+1=2为首项的等比数列.
∴a2n+2=2×2 n-1,∴a2n=2 n-2.
又a2n+a2n+1= a2n+2a2n+1=3a2n+1,∴数列{an}的前2007项的和为
a1+( a2+ a3)+ ( a4+ a5)+ ( a6+ a7)+ …+ ( a2006+ a2007)
= a1+(3a2+1)+ (3a4+1)+ (3a6+1)+ …+ (3a2006+1)
= 1+(3×2-5)+ (3×22-5)+ (3×23-5)+ …+ (3×21003-5)
= 1+(3×2-5)+ (3×22-5)+ (3×23-5)+ …+ (3×21003-5)
= 3×(2+22+23+…+21003+1-5×1003
=6×(21003-1)+1-5×1003=6×21003- 5020 ,故选D.
二、填空题
11.(命题人:启东中学)
在直三棱柱ABC-A1B1C1中,底面为直角三角形,ÐACB=90°,AC=6,BC=CC1=![]() ,P是BC1上一动点,则CP+PA1的最小值是___________.
,P是BC1上一动点,则CP+PA1的最小值是___________.
【解析】答案:5 .连A1B,沿BC1将△CBC1展开与△A1BC1在同一个平面内,连A1C,则A1C的长度就是所求的最小值.通过计算可得ÐA1C1C=90°.
又ÐBC1C=45°,\ÐA1C1C=135° 由余弦定理,可求得A1C=5.
12.(命题人:海门中学吴健,审题人:沈永飞 )
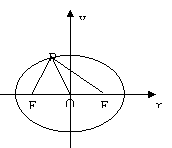
已知函数f(x)、g(x)满足x∈R时,f′(x)>g′(x),则x1<x2时,则f(x1)-f(x2)___
g(x1)-g(x2).(填>、<、=)
【解析】记![]() ,则
,则![]() .
.
由已知,![]() ,所以
,所以![]() 在R上单调递增,
在R上单调递增,
 所以x1<x2时,
所以x1<x2时,![]() ,即f(x1)-f(x2) < g(x1)-g(x2).
,即f(x1)-f(x2) < g(x1)-g(x2).
13.(命题人:通州中学王淦华,审题人:瞿国华)
△ABC内接于以O为圆心的圆,且![]() .
.
则 ![]() =
,
=
,![]() =
.
=
.
【解析】通过画图,可求![]() ,即
,即![]() 与
与![]() 的夹角,再
的夹角,再
通过圆心角与圆周角的关系,求得![]() ,而
,而![]() 是
是![]() 的一 半,可用半角公式进行计算.
的一 半,可用半角公式进行计算.
答案:![]() ,
,![]() .
.
14.(命题人:平潮高级中学吴杰,审题人:宋军)
若关于x的方程![]() 有不同的四解,则a的取值范围为
.
有不同的四解,则a的取值范围为
.
【解析】x=0是方程的一个根,其余根即方程![]() (x>0)的根.
(x>0)的根.
由f(x)=![]() (x>0)与y=1的交点个数,可知a>0.
(x>0)与y=1的交点个数,可知a>0.
且f(![]() )>1,得a>2.
)>1,得a>2.
15.(命题人:如东中学赵延贵,审题人:刘卫东)
已知![]() 为正整数,方程
为正整数,方程![]() 的两实根为
的两实根为![]() ,且
,且![]() ,则
,则![]() 的最小值为________________________.
的最小值为________________________.
【解析】提示:依题意,可知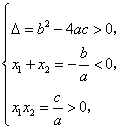 从而可知
从而可知![]() ,所以有
,所以有
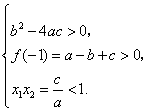
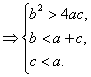 又
又![]() 为正整数,取
为正整数,取![]() ,则
,则
![]() ,所以
,所以![]() .从而
.从而![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,因此
,因此![]() 有最小值为
有最小值为![]() .
.
下面可证![]() 时,
时,![]() ,从而
,从而![]() ,所以
,所以![]() .
.
 又
又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
综上可得,![]() 的最小值为11.
的最小值为11.
16.(命题人:如东县马塘中学张志军,审题人:徐永华)
如图,在![]() 中,
中,![]() ,
,![]() ,
,
l为BC的垂直平分线,E为l上异于
D的一点,则![]() 等于____.
等于____.
【解析】![]() ,又
,又![]() ,
,
![]()
![]() .
.
17.(命题人:海安中学游余祥,审题人:王光华)
O为坐标原点,正△OAB中A、B在抛物线![]() 上,正△OCD中C、D在抛物线
上,正△OCD中C、D在抛物线![]() 上,则△ OAB与△OCD的面积之比为
.
上,则△ OAB与△OCD的面积之比为
.
【解析】设△OAB的边长为![]() ,则不妨设
,则不妨设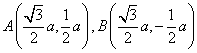 ,代入
,代入![]() ,得
,得

![]() ;同理,设△OCD的边长为
;同理,设△OCD的边长为![]() ,可得
,可得![]() .
.![]() ,
,![]() .
.
18.(命题人:南通中学陆玉英,审题人:顾军)
如图,在∠AOB的两边上分别为![]() ,
,
![]() 共9个点,连结线段
共9个点,连结线段![]() ,
,
如果其中两条线段不相交,则称之为一对“和睦线”,则图
中共有___________对“和睦线”
【解析】一个四边形,有且只有一对“和睦线”,这9个点可组成![]() 个四边形,故图中关于60对“和睦线”.
个四边形,故图中关于60对“和睦线”.
19.(命题人:南通一中秦志国)
已知二次函数f(x)=x2-2x+6,设向量a=(sinx,2),b=(2sinx,![]() ),c=(cos2x,1),d=(1,2).当x∈[0,π]时,不等式f(a·b)>f(c·d)的解集为___________.
),c=(cos2x,1),d=(1,2).当x∈[0,π]时,不等式f(a·b)>f(c·d)的解集为___________.
【解析】a·b=2sin2x+1≥1, c·d=cos2x+1≥1 ,f(x)图象关于x=1对称,
∴f(x)在(1,+∞)内单调递增.
由f(a·b)>f(c·d)![]() a·b>c·d,即2sin2x+1>2cos2x+1,
a·b>c·d,即2sin2x+1>2cos2x+1,
又∵x∈[0,π] ,∴x∈(![]() ).故不等式的解集为(
).故不等式的解集为(![]() ).
).
20.(命题人:南通市小海中学夏志辉,审题人:夏志辉)
设P为双曲线![]() 上除顶点外的任意一点,
上除顶点外的任意一点,![]() 分别为左右点,
分别为左右点,![]() 的内切圆交实轴于点M,则
的内切圆交实轴于点M,则![]() 值为
.
值为
.
【解析】 由已知,得 ![]() .
.
又![]() ,
,![]() .
.
因此![]() .
.
三、解答题
21.(命题人:海门中学吴健,审题人:沈永飞)
已知函数![]() 为实常数.
为实常数.
(1)a在什么范围内时,![]() 只有一个公共点?
只有一个公共点?
(2)若![]() 上有最小值2,求a的值.
上有最小值2,求a的值.
【解析】(1)![]() .
.
①当![]() 时,
时,![]() ,所以
,所以![]() 在R上单调增,此时
在R上单调增,此时![]() 只有一个公共点;
只有一个公共点;
②当![]() 时,
时,![]() .由
.由![]() ,得
,得![]() .
.
在![]() 上列表:
上列表:
|
|
|
|
|
|
|
|
| + | 0 | ─ | 0 | + |
|
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
因为![]() 只有一个公共点,所以
只有一个公共点,所以![]() 或
或![]() .
.
所以![]() ,得
,得![]() .
.
综上,![]() ,
,![]() 只有一个公共点.
只有一个公共点.
(2)![]() .
.
由![]() ,可知
,可知![]() 为偶函数,则原题即为
为偶函数,则原题即为![]() 在
在![]() 上有最小值2.
上有最小值2.
设![]() (
(![]() ),则
),则![]() .
.
①![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调增,所以
上单调增,所以![]() .
.
因为![]() 在
在![]() 上有最小值2,所以
上有最小值2,所以![]() ,所以
,所以![]() .
.
②![]() 时,
时,![]() ,无最小值,不合题意.
,无最小值,不合题意.
③![]() 时,
时,![]() ,
,![]() .
.
(I)![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调减,所以
上单调减,所以![]() ,
,
此时![]() 在
在![]() 上的最小值为
上的最小值为![]() ,不合.
,不合.
(II)![]() 时,由
时,由![]() ,得
,得![]() .
.
在![]() 上列表:
上列表:
|
|
|
|
| 2 |
|
| ─ | 0 | + | |
|
| ↘ | 极小值 | ↗ |
|
∴![]() .
.
综上,![]() 的值为
的值为![]() .
.
22.(命题人:海门市悦来中学邢素琴,审题人:董卫平)
设![]() =
=![]() (a>0)为奇函数,且
(a>0)为奇函数,且![]() min=
min=![]() ,数列{an}与{bn}满足如下关系:
,数列{an}与{bn}满足如下关系:
a1=2,![]() ,
,![]() .
.
(1)求f(x)的解析表达式;
(2)证明:当n∈N+时,有bn![]()
![]() .
.
【解析】(1)由f(x)是奇函数,得 b=c=0.
由f(x)min=![]() ,得a=2,故f(x)=
,得a=2,故f(x)= ![]() .
.
(2) ![]() =
=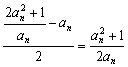 ,
,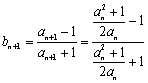 =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() =…=
=…=![]() .而b1=
.而b1=![]() ,∴
,∴![]() =
=![]() .
.
当n=1时,b1=![]() ,命题成立.
,命题成立.
当n≥2时,∵2n-1=(1+1)n-1=1+![]() ≥1+
≥1+![]() =n,
=n,
∴![]() <
<![]() ,即
bn≤
,即
bn≤![]() .
.
23.(命题人:通州中学陈颖,审题人:王淦华)
椭圆![]() 的两焦点为
的两焦点为![]() ,(
,(![]() 为坐标原点),P为椭圆上一点,
为坐标原点),P为椭圆上一点,![]() 的斜率分别为
的斜率分别为![]() 和
和![]() .
.
(1)求证:![]() ;
;
(2)若△![]() 的面积为3,求椭圆方程.
的面积为3,求椭圆方程.
【解析】解法一 (1) 依题意,
令![]() ,则
,则![]() .
.
∴![]() .∴
.∴![]() ,所以
,所以![]() .
.
(2)在Rt△![]() 中,
中,![]() ,
,
所以![]() .
.
所以椭圆方程为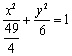 .
.
解法二 (1)令![]() ,由题意,得
,由题意,得
![]() , ①
, ① ![]() . ②
. ②
由①、②,可知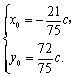
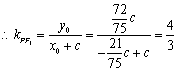 .
.
∴![]() ,∴
,∴![]() .
.
24.(命题人:通州中学陈颖,审题人:羌达勋)
某地区1986年以来人口总数和居民住宅总面积分别按等比数列和等差数列逐年递增.已知1986年底人均住房面积为10![]() ,2006年底人均住房面积为20
,2006年底人均住房面积为20![]() .据此计算:
.据此计算:
(1)1996年底人均住房面积超过14![]() ,试给出证明;
,试给出证明;
(2)若人口年平均增长率不超过3﹪,能否确保2008年底人均住房面积比2006年底有所增加?为什么?
【解析】(1)设86年底人口总数为a,住宅总面积10a,年人口增长的公比为![]() (即后一年是前一年人口的
(即后一年是前一年人口的![]() 倍),年住宅总面积的公差为
倍),年住宅总面积的公差为![]() ,则2006年底人均住房面积为
,则2006年底人均住房面积为![]() ,则
,则![]() ,故1996年底人均住房面积
,故1996年底人均住房面积![]() .
.
(2)2008年底人均住房面积![]() ,
,
2008年与2006年底人均住房面积之差![]() .
.
∵![]() ,∴只需考虑分子
,∴只需考虑分子![]() .
.
∵![]() ,∴
,∴![]() 单调递减.
单调递减.
又![]() ,
,
∴![]() .
.
∴![]() .
.
此即表明,2008年底人均住房面积仍超过2006年底人均住房面积.
25.(命题人:平潮高级中学吴杰,审题人:宋军)
已知焦点在x轴上的双曲线C的两条渐近线过坐标原点,且两条渐近线与以点![]() 为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称.
为圆心,1为半径为圆相切,又知C的一个焦点与A关于直线y=x对称.
(1)求双曲线C的方程;
(2)若Q是双曲线C上的任一点,F1、F2为双曲线C的左、右两个焦点,从F1引∠F1QF2的平分线的垂线,垂足为N,试求点N的轨迹方程;
(3)设直线y=mx+1与双曲线C的左支交于A、B两点,另一直线L经过M(-2,0)及AB的中点,求直线L在y轴上的截距b的取值范围.
【解析】(1)设双曲线C的渐近线方程为y=kx,即kx-y=0.
∵该直线与圆![]() 相切,∴双曲线C的两条渐近线方程为
相切,∴双曲线C的两条渐近线方程为![]() .
.
设双曲线C的方程为![]() ,∵双曲线C的一个焦点为
,∵双曲线C的一个焦点为![]() ,
,
∴![]() .∴双曲线C的方程为
.∴双曲线C的方程为![]() .
.
(2)若Q在双曲线的右支上,则延长QF2到T,使QT=OF1;
若Q在双曲线的左支上,则在QF2上取一点T,使QT=QF1.
根据双曲线的定义,TF2=2,所以点T在以F2![]() 为圆心,2为半径的圆上,即点T的轨迹方程是
为圆心,2为半径的圆上,即点T的轨迹方程是![]() . ①
. ①
由于点N是线段F1T的中点,设N(x,y),T(![]() ),
),
则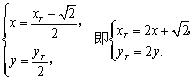
代入①并整理,得点N的轨迹方程为 ![]() .
.
(3)由![]() .令
.令![]() ,
,
直线与双曲线左支交于两点,等价于方程 ![]() 上有两个不等实根,
上有两个不等实根,
因此 .
.
又AB的中点为![]() ,∴直线L的方程为
,∴直线L的方程为![]() .
.
令x=0,得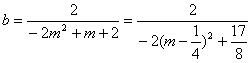 .
.
∵![]() ,∴
,∴![]() .
.
∴故b的取值范围是![]() .
.
26.(命题人:如东中学赵延贵,审题人:刘卫东)
已知![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,
, ![]() .
.
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)当n取何值时,![]() 取最大值,并求出最大值;
取最大值,并求出最大值;
(3)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【解析】(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即![]() .
.
又![]() ,可知对任何
,可知对任何![]() ,
,![]() ,所以
,所以![]() .
.
∵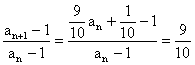 ,∴
,∴![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列.
的等比数列.
(2)由(I),可知![]() =
=![]() (
(![]() ).
).
∴![]() ,
,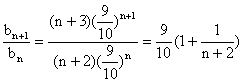 .
.
当n=7时,![]() ,
,![]() ;当n<7时,
;当n<7时,![]() ,
,![]() ;当n>7时,
;当n>7时,![]() ,
,![]() .
.
∴当n=7或n=8时,![]() 取最大值,最大值为
取最大值,最大值为![]() .
.
(3)由![]() ,得
,得![]() . (*)
. (*)
依题意,(*)式对任意![]() 恒成立,
恒成立,
①当t=0时,(*)式显然不成立,因此t=0不合题意.
②当t<0时,由![]() ,可知
,可知![]() (
(![]() ).
).
而当m是偶数时![]() ,因此t<0不合题意.
,因此t<0不合题意.
③当t>0时,由![]() (
(![]() ),
),
∴![]() ,∴
,∴![]() (
(![]() ).
).
设![]() (
(![]() ),
),
∵![]() =
=![]() ,
,
∴![]() .
.
∴![]() 的最大值为
的最大值为![]() .所以实数
.所以实数![]() 的取值范围是
的取值范围是![]() .
.
27.(命题人:如东中学葛张勇,审题人:刘卫东)
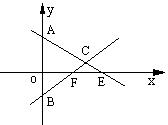 在△ABC中,已知A(0,1),B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且
在△ABC中,已知A(0,1),B(0,-1),AC、BC两边所在的直线分别与x轴交于E、F两点,且![]() =4.
=4.
(1)求点C的轨迹方程;
(2)若![]() ,
,
①试确定点F的坐标;
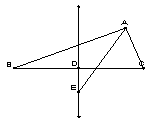
②设P是点C的轨迹上的动点,猜想△PBF的周长最大时点P的位置,并证明你的猜想.
【解析】(1)如图,设点C(x,y)(x≠0),E(xE,0),F(xF,0),由A,C,F三点共线,![]() ,xE=
,xE=![]() .同理,由B、C、F三点共线可得xF=
.同理,由B、C、F三点共线可得xF=![]() .
.
化简,得点C的轨迹方程为x2+4y2-4(x≠0).
 ∵
∵![]() =4,∴xE·xF=
=4,∴xE·xF=![]() =4.
=4.
(2)若![]() ,
,
①设F(xF,0),C(xC,yC),
∴![]()
![]() (xc,yc+1)=-8(xF-xc,yc).
(xc,yc+1)=-8(xF-xc,yc).
∴xc=![]() ,yC=
,yC=![]() .
.
代入x2+4y2=4, 得xF=±![]() .∴F(±
.∴F(±![]() ,0),即F为椭圆的焦点.
,0),即F为椭圆的焦点.
②猜想:取F(![]() ,0),设F1(-
,0),设F1(-![]() ,0)是左焦点,则当P点位于直线BF1与椭圆的交点处时,△PBF周长最大,最大值为8.
,0)是左焦点,则当P点位于直线BF1与椭圆的交点处时,△PBF周长最大,最大值为8.
证明如下:PF+PB=4-PF1+PB≤4+BF1,
∴△PBF的周长≤4+BF1+BF≤8.
28.(命题人:如东县马塘中学张志军,审题人:徐永华)
已知三角形ABC的两顶点A、B分别是曲线![]() 的左右焦点,且内角满足
的左右焦点,且内角满足![]() .
.
(1)求顶点C的轨迹方程E;
(2)若x轴上有两点![]() ,过N的直线与曲线E的交点是D、E.求
,过N的直线与曲线E的交点是D、E.求![]() 的值.
的值.
【解析】由![]() ,得
,得![]() ,
,![]() ,
,
所以顶点C的轨迹E的方程为![]() .
.
(2)设l:![]() (斜率不存在时不合题意),
(斜率不存在时不合题意),![]()
由![]() 得
得![]() ,则
,则![]() 时,有
时,有![]() .
.
![]()
![]() .
.
29.(命题人:如皋中学姚新国,审题人:薛钧)
第一行是等差数列0,1,2,3,…,2006,将其相邻两项的和依次写下作为第二行,第二行相邻两项的和依次写下作为第三行,依此类推,共写出2007行.
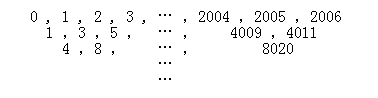
(1)求证:第1行至第2006行各行都构成等差数列.(定义只有两项的数列![]() 也称等差数列);
也称等差数列);
(2)各行的公差组成数列![]() .求通项公式
.求通项公式![]() ;
;
(3)各行的第一个数组成数列![]() ,求通项公式
,求通项公式![]() ;
;
(4)求2007行的这个数.
【解析】(1)记![]() 表示第
表示第![]() 行第
行第![]() 列的项.由已知知第1行是等差数列;
列的项.由已知知第1行是等差数列;
![]() ,
,
所以第2行数列是等差数列.
![]() ,
,
所以第3行数列是等差数列.
同理可证,第4,5,…,都是等差数列.
(2)![]() ,
,
![]() ,则
,则![]() 是等差数列,
是等差数列,![]() .
.
(3)![]() ,
,![]() .
.
∴数列![]() 是等差数列,
是等差数列,![]() ,所以
,所以![]() .
.
(4)![]() .
.
30.(命题人:如皋中学姚新国,审题人:刘建华)
已知集合![]() .
.
(1)求![]() ;
;
(2)若以![]() 为首项,
为首项,![]() 为公比的等比数列前
为公比的等比数列前![]() 项和记为
项和记为![]() ,对于任意的
,对于任意的![]() ,均有
,均有![]() ,求
,求![]() 的取值范围.
的取值范围.
【解析】(1)由![]() 得
得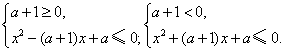
当![]() 时,
时,![]() .当
.当![]() 时,
时, ![]() ,当
,当![]() 时,
时,![]() .
.
综上,![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;当
;当![]() 时,
时, ![]() .
.
(2)当![]() 时,
时,![]() .而
.而![]() ,故
,故![]() 时,不存在满足条件的
时,不存在满足条件的![]() ;
;
当![]() 时,
时,![]() ,而
,而![]() 是关于
是关于![]() 的增函数,所以
的增函数,所以![]() 随
随![]() 的增大而增大,当
的增大而增大,当![]() 且无限接近
且无限接近![]() 时,对任意的
时,对任意的![]() ,
,![]() ,只须
,只须![]() 满足
满足
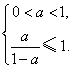 解得
解得![]() .
.
当![]() 时,
时,![]() .
.
显然![]() ,故不存在实数
,故不存在实数![]() 满足条件.
满足条件.
当![]() 时,
时,![]() .
.![]() ,适合.
,适合.
当![]() 时,
时,![]() .
.
![]() ,
,
![]() ,
,
![]() ,且
,且![]()
故![]() .
.
故只需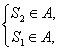 即
即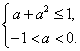 解得
解得![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.
31.(命题人:如皋一中潘佩,审题人:戴圩章)
设![]() 轴、
轴、![]() 轴正方向上的单位向量分别是
轴正方向上的单位向量分别是![]() 、
、![]() ,坐标平面上点
,坐标平面上点![]() 、
、![]()
![]() 分别满足下列两个条件:
分别满足下列两个条件:
①![]() 且
且![]() =
=![]() +
+![]() ;②
;②![]() 且
且![]() =
=![]() .
.
(1)求![]() 及
及![]() 的坐标;
的坐标;
(2)若四边形![]() 的面积是
的面积是![]() ,求
,求![]()
![]() 的表达式;
的表达式;
(3)对于(2)中的![]() ,是否存在最小的自然数M,对一切
,是否存在最小的自然数M,对一切![]() 都有
都有![]() <M成立?若存在,求M;若不存在,说明理由.
<M成立?若存在,求M;若不存在,说明理由.
【解析】(1)![]()
![]() .
.
![]()
![]()
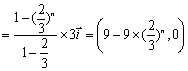 .
.
(2)![]()
![]() .
.
(3)![]()
![]() .
.
∴ ![]() ,
,![]() ,
,![]() .
.![]() ,
,
![]() ,
,![]() ,等等.
,等等.
即在数列![]() 中,
中,![]() 是数列的最大项,所以存在最小的自然数
是数列的最大项,所以存在最小的自然数![]() ,对一切
,对一切![]() ,都有
,都有![]() <M成立.
<M成立.
32.(命题人:海安中学游余祥,审题人:王光华)
函数![]() 的定义域为
的定义域为![]() ,设
,设![]() .
.![]()
![]()
(1)求证:![]() ;
;
(2)确定t的范围使函数![]() 在
在![]() 上是单调函数;
上是单调函数;
(3)求证:对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() ;并确定这样的
;并确定这样的![]() 的个数.
的个数.
【解析】(1)设![]() ,则
,则![]()
![]()
![]()
![]() ,所以
,所以![]() .
.
(2)![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() 时,
时,![]() ,
,![]() 是递增函数;
是递增函数;
当![]() 时,显然
时,显然![]() 在
在![]() 也是递增函数.
也是递增函数.
∵![]() 是
是![]() 的一个极值点,∴当
的一个极值点,∴当![]() 时,函数
时,函数![]() 在
在![]() 上不是单调函数.
上不是单调函数.
∴当![]() 时,函数
时,函数![]() 在
在![]() 上是单调函数.
上是单调函数.
(3)由(1),知![]() ,∴
,∴![]() .
.
又∵![]() , 我们只要证明方程
, 我们只要证明方程![]()
![]() 在
在![]() 内有解即可.
内有解即可.
记![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
∴![]() .
.
①当![]() 时,
时,![]() ,
,
方程![]() 在
在![]() 内有且只有一解;
内有且只有一解;
②当![]() 时,
时,![]() ,
,![]() ,
,
又![]() ,∴方程
,∴方程![]() 在
在![]() 内分别各有一解,方程
内分别各有一解,方程![]() 在
在![]() 内两解;
内两解;
③当![]() 时,方程
时,方程![]() 在
在![]() 内有且只有一解
内有且只有一解![]() ;
;
④当![]() 时,方程
时,方程![]() 在
在![]() 内有且只有一解
内有且只有一解![]() .
.
综上,对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() .
.
当![]() 时,满足
时,满足![]() ,
,![]() 的
的![]() 有且只有一个;
有且只有一个;
当![]() 时,满足
时,满足![]() ,
,![]() 的
的![]() 恰有两个.
恰有两个.
33.(命题人:南通一中朱柏华)
两名大学毕业生去某单位应聘,该单位要从参加应聘的人中录用5人,且两人同时被录用的概率为![]() .
.
(1)求参加应聘的人数;
(2)求两人中至少有一人被录用的概率.
【解析】(1)设参加应聘的人数为x,则![]() ,得x=20.
,得x=20.
(2)设两人中至少有一人被录用的概率为![]()
![]() ,则
,则![]() =1-
=1-![]() =
=![]() .
.
34.(命题人:南通市小海中学夏志辉,审题人:夏志辉)
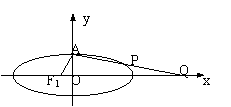
设椭圆![]() +
+![]() =1,a>b>0的左焦点为F1,上顶点为A,过点A与AF1垂直的直线分别交椭圆和x轴正半轴于P、Q两点,且P分向量
=1,a>b>0的左焦点为F1,上顶点为A,过点A与AF1垂直的直线分别交椭圆和x轴正半轴于P、Q两点,且P分向量![]() 所成的比为λ.
所成的比为λ.
(1)当λ∈(1,2)时,探求椭圆离心率(![]() -e)2的取值范围;
-e)2的取值范围;
(2)当λ=![]() 时,过A、Q、F1三点的圆恰好与直线L:x+
时,过A、Q、F1三点的圆恰好与直线L:x+![]() y+3=0相切,求椭圆的方程.
y+3=0相切,求椭圆的方程.
【解析】(1)设Q(x0,0),F1(-c,0),A(0,b),∵P分向量![]() 所成的比为λ,
所成的比为λ,
∴P(![]() ,
,![]() ),∴(
),∴(![]() )2
)2![]() +(
+(![]() )2
)2![]() =1. ①
=1. ①
而![]() =(c,b),
=(c,b),![]() =(x0,-b),
=(x0,-b),![]() ·
·![]() =0,∴cx0-b2=0. ②
=0,∴cx0-b2=0. ②
 由①、②消去x0,得(
由①、②消去x0,得(![]() )2
)2![]() +(
+(![]() )2=1,
)2=1,
即λ2![]() =(1+λ)2-1,即(
=(1+λ)2-1,即(![]() -e)2=1+
-e)2=1+![]() ∈(2,3).
∈(2,3).
(2)当λ=![]() 时,e-
时,e-![]() =-
=-![]() ,∴e=
,∴e=![]() ,a=2c.
,a=2c.
又∵△AF1Q是直角三角形,其外接圆圆心是斜边中点,
∴圆心为(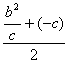 ,0)=(
,0)=(![]() ,0)=(c,0),
,0)=(c,0),
半径为r=![]() =
=![]() =a.
=a.
由圆恰好与直线L:x+![]() y+3=0相切,得
y+3=0相切,得![]() =a,∴a=2,b=
=a,∴a=2,b=![]() .
.
∴椭圆方程为![]() +
+![]() =1.
=1.
35.(命题人:南通市小海中学夏志辉,审题人:夏志辉)
设一动点M在x轴正半轴上,过动点M与定点![]() 的直线交y=x(x>0)于点Q,动点M在什么位置时,
的直线交y=x(x>0)于点Q,动点M在什么位置时,![]() 有最大值,并求出这个最大值.
有最大值,并求出这个最大值.
【解析】 设![]() ,要它与
,要它与![]() 相交,则
相交,则![]() .
.
令![]() ,令
,令![]() ,得
,得![]() .
.
∴![]() .
.
∴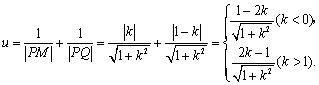
于是![]() .
.
由![]() ,∴
,∴![]() .
.
而当l的方程为x=2时,u=2,
∴![]() 对应得k=-2,进而求得
对应得k=-2,进而求得![]() .
.