高三数学第一学期期末质量调研试题
命题人:杨敏忠 孙福明 审卷人:于新华 徐淮源 周敏泽
注意事项
考生在答题前请认真阅读本注意事项及各题答题要求
1.本试卷分为第Ⅰ卷(必做题)和第Ⅱ卷(附加题)两部分.第Ⅰ卷(必做题)包括选择题和解答题两种题型,满分为160分,考试时间为120分钟;第Ⅱ卷(附加题)由解答题组成,满分40分,考试时间为30分钟.选修历史的考生只需完成第Ⅰ卷(必做题),选修物理的考生需完成第Ⅰ卷(必做题)和第Ⅱ卷(附加题).
2.请将本试卷答案做在答题卡上的指定位置,在其它位置作答一律无效.
第I卷(必做题)
一、填空题:本大题共14小题,每小题5分,共70分.
1.函数![]() 的最小正周期是 ▲ .
的最小正周期是 ▲ .
2. 抛物线![]() 的焦点坐标是 ▲ .
的焦点坐标是 ▲ .
3. 已知复数![]() 满足(
满足(![]() +2i)
+2i)![]() =5(i为虚数单位),则
=5(i为虚数单位),则![]() =____▲____.
=____▲____.
 4.已知
4.已知![]() ,则
,则![]() 值为
▲ .
值为
▲ .
5. 右边是根据所输入的![]() 值计算
值计算![]() 值的一个算法程序, 若
值的一个算法程序, 若![]() 依次取数列
依次取数列![]()
![]() 中的前200项,则所得
中的前200项,则所得![]() 值中的最小值为 ▲ .
值中的最小值为 ▲ .
6. 已知一正方体的棱长为![]() ,表面积为
,表面积为![]() ;一球的半径为
;一球的半径为![]() 表面积为
表面积为![]() ,若
,若![]() ,则
,则![]() = ▲ .
= ▲ .
7. 某人有甲乙两只电子密码箱,欲存放三份不同的重要文件,则此人使用同一密码箱存放放这三份重要文件的概率是 ▲ .
8. 若![]() ,试写出方程
,试写出方程![]() 表示双曲线的一个充分不必要条件 ▲ .
表示双曲线的一个充分不必要条件 ▲ .
9. 已知样本![]() 的平均数是
的平均数是![]() ,标准差是
,标准差是![]() ,则
,则![]() 的值为 ▲ .
的值为 ▲ .
10.
若函数![]() 在
在![]() 上有意义,则实数
上有意义,则实数![]() 的取值范围是 ▲ .
的取值范围是 ▲ .
11. 两个正数![]() 的等差中项是5,等比中项是4.若
的等差中项是5,等比中项是4.若![]() ,则椭圆
,则椭圆![]() 的离心率e的大小为 ▲ .
的离心率e的大小为 ▲ .
12. 已知向量![]() 直线l过点
直线l过点![]() 且与向量
且与向量![]() 垂直,则直线l的一般方程是 ▲ .
垂直,则直线l的一般方程是 ▲ .
13. 已知![]() 均为实数,设数集
均为实数,设数集![]() ,且A、B都是集合
,且A、B都是集合![]() 的子集.如果把
的子集.如果把![]() 叫做集合
叫做集合![]() 的“长度”,那么集合
的“长度”,那么集合![]() 的“长度”的最小值是 ▲ .
的“长度”的最小值是 ▲ .
14.设![]() 为正整数,两直线
为正整数,两直线![]() 的交点是
的交点是![]() ,对于正整数
,对于正整数![]() ,过点
,过点![]() 的直线与直线
的直线与直线![]() 的交点记为
的交点记为![]() .则数列
.则数列![]() 通项公式
通项公式![]() =
▲
.
=
▲
.
二、解答题:本大题共6小题,共90分,解答时需写出文字说明、证明过程或演算步骤.
15. (本小题满分14分)
在![]() 中,
中, ![]() 所对边分别为
所对边分别为![]() .
.
已知![]()
![]() ,且
,且![]() .
.
(Ⅰ)求![]() 大小.
大小.
(Ⅱ)若![]() 求
求![]() 的面积S的大小.
的面积S的大小.
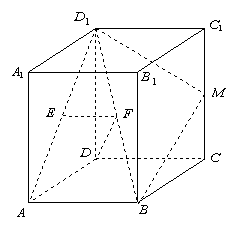 16. (本小题满分15分)
16. (本小题满分15分)
如图,已知长方体![]() 底面
底面![]() 为正方形,
为正方形,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点.
的中点.
(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)设![]() 的中点,当
的中点,当![]() 的比值为多少时,
的比值为多少时,![]() 并说明理由.
并说明理由.
17. (本小题满分15分)
已知圆C与两坐标轴都相切,圆心C到直线![]() 的距离等于
的距离等于![]() .
.
(Ⅰ)求圆C的方程.
(Ⅱ)若直线![]()
![]() 与圆C相切,求证:
与圆C相切,求证:![]()
18. (本小题满分14分)
为了研究某高校大学新生学生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列![]() 的前四项,后6组的频数从左到右依次是等差数列
的前四项,后6组的频数从左到右依次是等差数列![]() 的前六项.
的前六项.
(Ⅰ)求等比数列![]() 的通项公式;
的通项公式;
(Ⅱ)求等差数列![]() 的通项公式;
的通项公式;
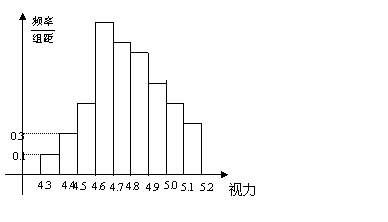 (Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率
(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率![]() 的大小.
的大小.
19.(本小题满分16分)
已知函数![]() 的导数
的导数![]()
![]()
![]() 为实数,
为实数,![]() .
.
(Ⅰ)若![]() 在区间
在区间![]() 上的最小值、最大值分别为
上的最小值、最大值分别为![]() 、1,求
、1,求![]() 、
、![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求经过点![]() 且与曲线
且与曲线![]() 相切的直线
相切的直线![]() 的方程;
的方程;
(Ⅲ)设函数![]() ,试判断函数
,试判断函数![]() 的极值点个数.
的极值点个数.
20. (本小题满分16分)
数列![]() 中,
中,![]() ,其前
,其前![]() 项的和为
项的和为![]() .
.
(Ⅰ)设![]() ,求证:数列
,求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求![]() 的表达式;
的表达式;
(Ⅲ)求证:![]() .
.
第Ⅱ卷(附加题)
注意事项: 1.附加题包括必考题和选考题,第1、2题为必考题,每个考生都必须做答.第3、4、5、6题为选考题,考生根据要求做答.
2.附加题满分为40分,考试时间为30分钟,解答时需写出文字说明、证明过程或演算步骤.
一、必做题:
1. (本小题满分10分)
如图,在三棱锥![]() 中,顶点
中,顶点![]() 在空间直角坐标系的原点处,顶点
在空间直角坐标系的原点处,顶点![]() 分别在
分别在![]() 、
、![]() 、
、![]() 轴上,
轴上, ![]() 是
是![]() 的中点,且
的中点,且![]() ,∠
,∠![]() .
.
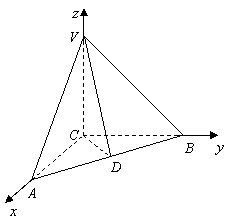 (Ⅰ)当
(Ⅰ)当![]() 时,求向量
时,求向量![]() 与
与![]() 夹角
夹角![]() 的余弦值的大小;
的余弦值的大小;
(Ⅱ)当角![]() 变化时,求直线
变化时,求直线![]() 与平面
与平面![]() 所成角的取值范围.
所成角的取值范围.
2.(本小题满分10分)
在一个盒子中,放有标号分别为![]() ,
,![]() ,
,![]() ,4的四个小球,现从这个盒子中,有放回地先后摸出两个小球,它们的标号分别为
,4的四个小球,现从这个盒子中,有放回地先后摸出两个小球,它们的标号分别为![]() 、
、![]() ,记
,记![]() .
.
(Ⅰ)求随机变量![]() 的分布列;
的分布列;
(Ⅱ)求随机变量![]() 的数学期望;
的数学期望;
(Ⅲ)设“函数![]()
![]()
![]()
![]() (
(![]() )在区间
)在区间![]() 上有且只有一个零点”为事件
上有且只有一个零点”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
二、选做题:请考生在第3、4、5、6题中任选两题作答.如果多做,则以第3、4两题记分.
3. (本小题满分10分)
 从⊙
从⊙![]() 外一点
外一点![]() 向圆引两条切线
向圆引两条切线![]() 、
、![]() (
(![]() 、
、![]() 为切点)和割线
为切点)和割线![]()
![]() 与⊙
与⊙![]() 交于
交于![]() 、
、![]() 两点
两点![]() 从
从![]() 点作弦
点作弦![]() 平行于
平行于![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,连结
,连结![]() ,
,
求证:(Ⅰ)![]() ;
;
(Ⅱ)![]() .
.
4. (本小题满分10分)
给定矩阵![]() =
=![]() ,
,![]() =
=![]() .
.
(Ⅰ)求![]() 的特征值
的特征值![]() ,
,![]() 及对应特征向量
及对应特征向量![]() ,
,
(Ⅱ)求![]() .
.
5.(本小题满分10分)
设点![]() 为坐标原点,直线
为坐标原点,直线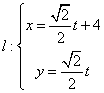
![]() 与曲线
与曲线![]() :
:![]() (参数
(参数![]() )交于
)交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求直线![]() 与曲线
与曲线![]() 的普通方程;
的普通方程;
(Ⅱ)求证:![]() .
.
6.(本小题满分10分)
已知关于![]() 的不等式
的不等式![]() (
(![]() ).
).
(Ⅰ)当![]() 时,求此不等式的解集;
时,求此不等式的解集;
(Ⅱ)若此不等式的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.