高三数学第一学期第3次月考试卷
一、填空(4¢×12=48¢)
1.若角x=-arccos![]() ,则tg2x= 。
,则tg2x= 。
2.不等式x<a的一个充分条件为0<x<1,则a的取值范围为 。
3.数列{![]() }的通项公式为
}的通项公式为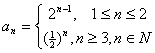 ,则
,则![]() 。
。
4.若复数z=sin2![]() 1+
1+![]() 为纯虚数,则角θ组成的集合为 。
为纯虚数,则角θ组成的集合为 。
5.已知函数![]() ,若f(x0)>1,则x0
,若f(x0)>1,则x0![]() 。
。
6.△ABC中,若![]() ,则△ABC为 三角形。
,则△ABC为 三角形。
7.(川中班)(理)在极坐标系中,A(1,![]() ),点B在直线ρcosθ+ρsinθ=0上运动,当线
),点B在直线ρcosθ+ρsinθ=0上运动,当线
段AB长最短时,点B的极坐标为 。
(川中班)(文)实数x、y满足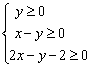 ,则
,则![]() 的取值范围为 。
的取值范围为 。
(川中南校班) ![]() 。
。
8.若数列{an}为等差数列,a1>0,a2005+a2004>0,a2005·a2004<0,则使前n项和Sn>0的最大自然数n= 。
9.若a,b![]() ,则使
,则使![]() 恒成立的最小正数m= 。
恒成立的最小正数m= 。
10.6人分乘两辆出租车,每辆最多四人,则甲、乙两人坐在同一辆车的概率为 。
(答案用分数表示)
11.规定a△b=![]() ,a、b
,a、b![]() ,若1△k=3,则函数f(x)=k△x的值域为 。
,若1△k=3,则函数f(x)=k△x的值域为 。
12.为了保证信息安全传输,有一种称为秘密密钥密码系统,其加密、解密原理如下图:
![]()
明文 密文 密文 明文,
现在加密密钥为y=loga(x+2),如下所示:明文“6”通过加密后得到密文“3”,
再发送,接受方通过解密密钥解密得明文“6”,问“接受方接到密文”4“,则解密
后得到明文为 。
二、选择(4¢×4=16)
13.已知数列{an}中,an=an (a>0),则![]() ( )
( )
(A)-1; (B)-1或![]() ; (C)-1或
; (C)-1或![]() 或2; (D)不能确定。
或2; (D)不能确定。
14.若log![]() ,则sinx的取值范围为 ( )
,则sinx的取值范围为 ( )
(A)![]() ; (B)
; (B)![]() ;
;
(C)![]()
![]()
![]() ; (D)
; (D)![]()
![]()
![]() 。
。
15.已知f(x)是周期为2的奇函数,当x![]() 时,f(x)=2x,则f
时,f(x)=2x,则f![]() 值 (
)
值 (
)
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() 。
。
16.关于函数f(x)=sin2x![]() ,有下列四个结论:
,有下列四个结论:
① f(x)为偶函数; ② 当x>2003时,f(x) >![]() 恒成立;
恒成立;
③ f(x)的最大值为![]() ; ④ f(x)的最小值为
; ④ f(x)的最小值为![]() 。其中结论正确个数为 ( )
。其中结论正确个数为 ( )
(A)1个; (B)2个; (C)3个; (D)4个。
三、解答题(10+12¢+14¢+16¢+16¢+18¢)
17.已知A=![]() ,B=
,B=![]()
(1)求A; (2)若A![]() ,求a的取值范围。
,求a的取值范围。
解:
18.某客运公司买了每辆2a万元的大客车投入运营,根据调查得知,每辆客车每年客运收
入约为a万元,且每辆客车第n年的油料费,维修费及其他各种管理费用总和P(n)(万
元)与年数n成正比,又知第3年每辆客车上述费用是该年客运收入的48%。
(1)写出每辆客车运营的总利润y(万元)与n的函数表达式;
(2)每辆客车运营多少年可使其运营的年平均利润最大?
解:
19.已知:z1=2cosx+![]() sinx,z2=a+b
sinx,z2=a+b![]() ,a、b
,a、b![]() ,
,![]() 为虚数单位,f(x)=cosx·Re
为虚数单位,f(x)=cosx·Re![]()
且f(0)=2,f![]() ,
,
(1)求z2 ;
(2)求函数f(x)在(![]() 上的单调递增区间;
上的单调递增区间;
(3)若![]() ,且
,且![]() ,求
,求![]() 的值。
的值。
解:
20.设f(k)是满足不等式log2x+log2(3·2k-1-x)≥2K-1,(k![]() 的自然数x的个数,
的自然数x的个数,
(1)求f(x)的解析式;
(2)记Sn=f(1)+f(2)+……+f(n),求Sn解析式;
(3)记Pn=n-1,设Tn=![]() ,对任意n
,对任意n![]() 均有Tn<m成立,
均有Tn<m成立,
求出整数m的最小值。
解:
21.给出函数封闭的定义:若对于定义域D内的任一个自变量x0,都有函数值f(x0)![]() ,则
,则
称函数y=f(x)在D上封闭。
(1)若定义域D1=(0,1),判断下列函数中哪些在D1上封闭,且给出推理过程
f1(x)=2x-1,f2(x)=![]() ,f3(x)=2x-1,f4(x)=cosx.;
,f3(x)=2x-1,f4(x)=cosx.;
(2)若定义域D2=(1,2),是否存在实数a使函数f(x)=![]() 在D2上封闭,若存在,
在D2上封闭,若存在,
求出a的值,并给出证明,若不存在,说明理由。
解:
22.函数f(x)满足2f(x)-f![]() =4x
=4x![]() ,数列{an}和{bn}满足下列条件:a1=1,an+1=2an+f(n),
,数列{an}和{bn}满足下列条件:a1=1,an+1=2an+f(n),
bn=an+1-an,n![]() ;
;
(1)f(x)的解析式;
(2)求数列bn的通项公式;
(3)试比较2an与bn的大小,且证明你的结论。
解:
高三数学第一学期第3次月考试卷解答
1
一、填空(4¢×12=48¢)
1.若角x=-arccos![]() ,则tg2x= -24/7 。
,则tg2x= -24/7 。
2.不等式x<a的一个充分条件为0<x<1,则a的取值范围为 a≥1 。
3.数列{![]() }的通项公式为
}的通项公式为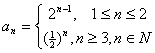 ,则
,则![]() 55/18 。
55/18 。
4.若复数z=sin2![]() 1+
1+![]() 为纯虚数,则角θ组成的集合为
为纯虚数,则角θ组成的集合为![]() 。
。
5.已知函数![]() ,若f(x0)>1,则x0Î (-¥ ,-1)È(1,+¥) 。
,若f(x0)>1,则x0Î (-¥ ,-1)È(1,+¥) 。
6.△ABC中,若![]() ,则△ABC为 等腰直角 三角形。
,则△ABC为 等腰直角 三角形。
7.(川中班)(理)在极坐标系中,A(1,![]() ),点B在直线ρcosθ+ρsinθ=0上运动,当线
),点B在直线ρcosθ+ρsinθ=0上运动,当线
段AB长最短时,点B的极坐标为 (![]() ,
,![]() ) 。
) 。
(川中班)(文)实数x、y满足
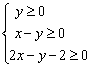 ,则
,则![]() 的取值范围为 [
的取值范围为 [![]() ,1] 。
,1] 。
(川中南校班) ![]()
![]() 。
。
8.若数列{an}为等差数列,a1>0,a2005+a2004>0,a2005·a2004<0,则使前n项和Sn>0的最大
自然数n= 4008 。
9.若a,b![]() ,则使
,则使![]() 恒成立的最小正数m=
恒成立的最小正数m= ![]() 。
。
10.6人分乘两辆出租车,每辆最多四人,甲、乙两人坐在同一辆车的概率为 ![]() 。
。
(答案用分数表示)
11.规定a△b=![]() ,a, b
,a, b![]() ,若1△k=3,则函数f(x)=k△x的值域为 (1,+¥ ) 。
,若1△k=3,则函数f(x)=k△x的值域为 (1,+¥ ) 。
12.为了保证信息安全传输,有一种称为秘密密钥密码系统,其加密、解密原理如下图:
![]()
明文 密文 密文 明文,
现在加密密钥为y=loga(x+2),如下所示:明文“6”通过加密后得到密文“3”,
再发送,接受方通过解密密钥解密得明文“6”,问“接受方接到密文”4“,则解密后得
到明文为 14 。
二、选择(4¢×4=16)
13.已知数列{an}中,an=an
(a>0),则![]() ( C )
( C )
(A)-1; (B)-1或![]() ;
;
(C)-1或![]() 或2; (D)不能确定。
或2; (D)不能确定。
14.若log![]() ,则sinx的取值范围为 ( B )
,则sinx的取值范围为 ( B )
A)![]() ; (B)
; (B)![]() ;
;
(C)![]()
![]()
![]() ; (D)
; (D)![]()
![]()
![]() 。
。
15.已知f(x)是周期为2的奇函数,当x![]() 时,f(x)=2x,则f
时,f(x)=2x,则f![]() 值为 ( B )
值为 ( B )
(A)![]() ; (B)
; (B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() 。
。
16.关于函数f(x)=sin2x![]() ,有下列四个结论:
,有下列四个结论:
① f(x)为偶函数; ② 当x>2003时,f(x) >![]() 恒成立;
恒成立;
③ f(x)的最大值为![]() ; ④ f(x)的最小值为
; ④ f(x)的最小值为![]() 。其中结论正确个数为 ( B
)
。其中结论正确个数为 ( B
)
(A)1个; (B)2个; (C)3个; (D)4个。
三、解答题(10+12¢+14¢+16¢+16¢+18¢)
17.已知A=![]() ,B=
,B=![]()
(1)求A; (2)若A![]() ,求a的取值范围。
,求a的取值范围。
解:(1)A=![]() ,Þ A=(-¥,-3)È[4,+¥);
,Þ A=(-¥,-3)È[4,+¥);
(2)B=![]() ,Þ
,Þ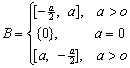 ,∵A
,∵A![]() ,
,
当a>0时,Þ![]() ,Þ 0<a<4; 当a=0时,Þ A
,Þ 0<a<4; 当a=0时,Þ A![]() ,Þ a=0,
,Þ a=0,
当a<0时,Þ![]() ,Þ -3≤a<0; 综上,Þ -3≤a<4
,Þ -3≤a<0; 综上,Þ -3≤a<4
18.某客运公司买了每辆2a万元的大客车投入运营,根据调查得知,每辆客车每年客运收
入约为a万元,且每辆客车第n年的油料费,维修费及其他各种管理费用总和P(n)(万
元)与年数n成正比,又知第3年每辆客车上述费用是该年客运收入的48%。
(1)写出每辆客车运营的总利润y(万元)与n的函数表达式;
(2)每辆客车运营多少年可使其运营的年平均利润最大?
解:(1)∵客车第n年的各种费用总和P(n)与年数n成正比,设![]() ,k为待定常数,
,k为待定常数,
∵第3年费用是该年客运收入的48%,Þ![]() ,∴
,∴![]() ,Þ
,Þ![]() ,
,
∴运营的总利润![]() ,nÎN
,nÎN
(2)![]() ,
,
当且仅当![]() 时成立,nÎN,Þ n2=25,Þ n=5,∴运营5年可使其运营的年平
时成立,nÎN,Þ n2=25,Þ n=5,∴运营5年可使其运营的年平
均利润最大且最大值为0.12a 。
19.已知:z1=2cosx+![]() sinx,z2=a+b
sinx,z2=a+b![]() ,a、b
,a、b![]() ,
,![]() 为虚数单位,f(x)=cosx·Re
为虚数单位,f(x)=cosx·Re![]()
且f(0)=2,f![]() ,
,
(1)求z2 ;
(2)求函数f(x)在![]() 上的单调递增区间;
上的单调递增区间;
(3)若![]() ,且
,且![]() ,求
,求![]() 的值。
的值。
解:(1)z2=a+bi,a、bÎR,![]()
ÞRe![]()
![]() ,Þ
,Þ![]()
![]() ,∵
,∵![]() ,Þ
,Þ![]() ,Þ z2=1+2
,Þ z2=1+2![]() ;
;
(2)![]() ,∵xÎ
,∵xÎ![]() ,∴
,∴![]() ,
,
Þ![]() ,或
,或![]() ,或
,或![]() ,函数单调递增,
,函数单调递增,
Þ 在![]() 、或
、或![]() 、或
、或![]() 上,函数单调递增;
上,函数单调递增;
∴函数f(x)在![]() 上的单调递增区间为:(-p,-
上的单调递增区间为:(-p,-![]() ]、[-
]、[-![]() ,
,![]() ]、[
]、[![]() ,p) 。
,p) 。
(3)![]() Þ
Þ![]() ,Þ
,Þ![]() 或
或![]() ,
,
kÎZ,Þ![]() 或
或![]() ,kÎZ,∵
,kÎZ,∵![]() ,Þ
,Þ![]() ,kÎZ,Þ
,kÎZ,Þ
![]() 。
。
20.设f(k)是满足不等式log2x+log2(3·2k-1-x)≥2K-1,(k![]() 的自然数x的个数,
的自然数x的个数,
(1)求f(x)的解析式;
(2)记Sn=f(1)+f(2)+……+f(n),求Sn解析式;
(3)记Pn=n-1,设Tn=![]() ,对任意n
,对任意n![]() 均有Tn<m成立,
均有Tn<m成立,
求出整数m的最小值。
解:(1)原不等式ó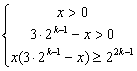 ó
ó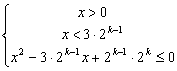
ó![]() (4分)Þ
(4分)Þ![]() . (6¢)
. (6¢)
(2)![]() . (10¢)
. (10¢)
(3)![]() , (12¢)
, (12¢)
当1≤n≤9时,![]() ¯,此时
¯,此时![]() , (14¢)
, (14¢)
当n≥10时,![]() ¯,此时
¯,此时![]() ,
,
∴![]() ,
,![]() . (16¢)
. (16¢)
21.给出函数封闭的定义:若对于定义域D内的任一个自变量x0,都有函数值f(x0)![]() ,则
,则
称函数y=f(x)在D上封闭。
(1)若定义域D1=(0,1),判断下列函数中哪些在D1上封闭,且给出推理过程
f1(x)=2x-1,f2(x)=![]() ,f3(x)=2x-1,f4(x)=cosx.;
,f3(x)=2x-1,f4(x)=cosx.;
(2)若定义域D2=(1,2),是否存在实数a使函数f(x)=![]() 在D2上封闭,若存在,
在D2上封闭,若存在,
求出a的值,并给出证明,若不存在,说明理由。
解:(1)∵f1(![]() )=0Ï(0,1),∴f(x)在D1上不封闭;(2¢)
)=0Ï(0,1),∴f(x)在D1上不封闭;(2¢)
∵f2(x)=-(x+![]() )2+
)2+![]() 在(0,1)上是减函数,∴0<f2(1)<f2(x)<f2(0)=1,
在(0,1)上是减函数,∴0<f2(1)<f2(x)<f2(0)=1,
∴f2(x)Î(0,1)Þf2(x)在D1上封闭;(4¢)
∵f3(x)=2x-1在(0,1)上是增函数,∴0=f3(0)<f3(x)<f3(1)=1,
∴f3(x)Î(0,1)Þf3(x)在D1上封闭;(6¢)
∵f4(x)=cosx在(0,1)上是减函数,∴cos1=f4(1)<f4(x)<f4(0)=1,
∴f4(x)Î(cos1,1)Ì(0,1)Þf4(x)在D1上封闭;(8¢)
(2)f(x)=5-![]() ,假设f(x)在D2上封闭,对a+10讨论如下:
,假设f(x)在D2上封闭,对a+10讨论如下:
若a+10>0,则f(x)在(1,2)上为增函数,故应有![]() Þa=2 (10¢)
Þa=2 (10¢)
若a+10=0,则f(x)=5,此与f(x)Î(1,2)不合,(12¢)
若a+10<0,则f(x)在(1,2)上为减函数,故应有![]() ,无解,(14¢)
,无解,(14¢)
综上可得,a=2时f(x)在D2上封闭.
22.函数f(x)满足2f(x)-f![]() =4x
=4x![]() ,数列{an}和{bn}满足下列条件:a1=1,an+1=2an+f(n),
,数列{an}和{bn}满足下列条件:a1=1,an+1=2an+f(n),
bn=an+1-an,n![]() ,
,
(1)f(x)的解析式;
(2)求数列bn的通项公式;
(3)试比较2an与bn的大小,且证明你的结论。
解:(1)![]() (4¢)
(4¢)
(2)由题设,an+1=2an+2n+1 ①, an+2=2an+1+2n+3 ②, ②-①:an+2-an+1=2(an+1-an)+2 (6¢)
即bn+1=2bn+2Þbn+1+2=2(bn+2),∴{bn+2}为等比数列,q=2,b1=a2-a1=4 (8¢)
bn+2=6·2n-1Þbn=3·2n-2 (10¢)
(3)由上,an+1-an=3·2n-2 ③,an+1-2an=2n+1 ④,③-④:an=3·2n-2n-3 (12)
∴2an-bn=3·2n-4n-4.
n=1时,2a1-b1=-2<0,此时2an<bn;
n=2时,2a2-b2=0,此时2an=bn; (14¢)
n≥3时,3·2n=3(1+1)n=3(1+C![]() +C
+C![]() +…+C
+…+C![]() +C
+C![]() )>3(1+C
)>3(1+C![]() +C
+C![]() )=6n+3>4n+4,
)=6n+3>4n+4,
此时,2an>bn.
综上可得:当n=1时,2an<bn,当n=2时,2an=bn,当n≥3时,2an>bn. (18¢)