高三数学第一学期第4次月考试卷
一、填空（4¢×12=48¢）
1．函数y=
的定义域为
。
2．计算：arc cos(cos
)=
。
3．已知集合 A={xx2＜16}，B={xx≥a}，若A∩B=Æ，则实数a的取值范围是 。
4．已知a、b、c是锐角三角形ABC中角A、B、C的对边，若b=2，c=3，且△ABC的面积为
，
则a= 。
5．（理）
展开式中含有常数项，则正整数n的最小值为
。
（文）在等差数列{an}中，已知a3=2，则a1+a2+a3+a4+a5= 。
6．（理）圆ρ=cosθ-sinθ，（ρ＞0，0≤θ＜2π）的圆心的极坐标是 。
（文）在条件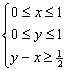
下，使ω=y-2x取得最大值时的点的坐标是 。
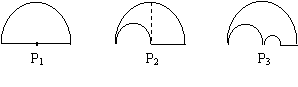7．如图P1是一块半径为1的半圆形纸板，在P1的左下端剪去一个半径为
的半圆得图形P2，然后依次剪去一个更小的半圆（其直径为前一个被剪掉半圆的半径），得图形P3、P4、…、Pn、…。记纸板Pn的面积为Sn，则
。
8．浦东新区二期课改经验交流会打算交流试点学校的论文5篇和非试点学校的论文3篇，排列次序可以任意排列，则最先和最后交流的论文不能来自同类学校的概率是 。
9．已知xÎC，且
，则
= 。
10．设数列{an}的前n项和为Sn，令Tn=
，称Tn为数列a1、a2、…、an的理想数。
已知a1、a2、a3、…、a500的理想数为2004，那么数列6、a1、a2、a3、…、a500的理想数为 。
|
,例如：1*2=1，3*2=2，则函数
的值域为
。
12．已知数列
，把数列{an}的各项排成如右三角形形状，
记A（m，n)表示第m行、第n列的项，则A(10，5)= 。
二、选择（4¢×4=16）
13．已知A={yy=
}，B={yy=
，
，则A
为 （ ）
（A）
； （B）
； （C）[0，]； （D）
。
14．若奇函数f(x)在（0，+∞）是增函数，又f(-3)=0，则{x
＜0}的解集为 （ ）
（A）（-3,0）∪（3, +∞）； （B）（-3,0）∪（0,3）；
（C）（-∞,-3）∪（3,+∞）； （D）(-∞,-3)∪（0,3）。
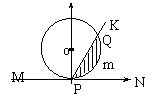
15．如图是半径为2的圆，切直线于点P，射线PK从PN出发，
绕P点按逆时钟方向旋转到PM，旋转过程中，PK交圆于
点Q，设OP按逆时钟方向旋转到OQ所形成的角为x，
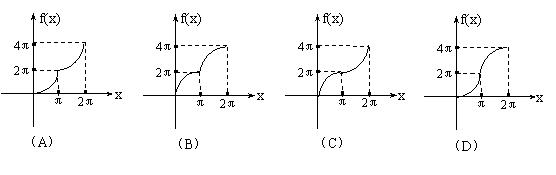
设弓形PmQ的面积为S=f(x)，那么f(x)的图形大致是 （ ）
 |
16．定义在R上函数f(x)既是偶函数，又是周期函数，若f(x)的最小正周期为π，
当xÎ [0，
时，f(x)=sinx，则f(
)的值为 （ ）
（A）； （B）-； （C）-
； （D）。
三、解答题（12¢+12¢+14¢+14¢+16¢+18¢）
17．已知
。
(1)化简f(x)；
(2)若f(x)=
，
，求x；
(3)求出f(x)的值域。
解：
18．已知z为虚数，且2z+15=
。
⑴求z；
⑵设u=(3
)z，若u在复平面上的对应点在第二、四象限的角平分线上，求复数z；
⑶若z2+2
为实数，且z恰好为实系数方程x2+px+q=0的两根，试写出此方程。
解：
19．2005年禽流感的爆发，给某疫区禽类养殖户带来了较大的经济损失，某养殖户原来投资共25万，第一个月损失的金额为投资额的
，以后由于政府重视，积极防治，疫情趋缓，从第二个月起，每一个月的损失是上月损失的
。问：
(1)前三个月中，该养殖户总共损失金额多少万元？
(2)为了维护养殖专业户的利益，政府除了加大防治力度，扑灭疫情之外，还决定给养殖
户一定的经济补偿，该养殖户每月底可向政府领取1.2万元的补偿金，并且每一个月
损失的金额（未补贴前）是上月损失金额的（补贴后）的，问接受了政府补贴后，
该养殖户第3个月损失多少元？又问：与(1)相比较，该养殖户在三个月当中总共可减
少损失多少元？
解：
20．已知f(x)=2x+1，将f(x)的反函数y=f—1(x)的图象向上平移1个单位后，再向右平移2个单位，就得到函数y=g(x)的图象。
(1)写出y=g(x)的解析式；
(2)若h(x)
，求F(x)=h(x)-g(x)的最值。
解：
21．⑴证明：当a＞1时，不等式
成立。
⑵要使上述不等式成立，能否将条件“a＞1”适当放宽？若能，请放宽条件并简述理由；若不能，也请说明理由。
⑶请你根据⑴、⑵的证明，试写出一个类似的更为一般的结论，且给予证明。
解：
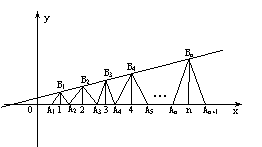
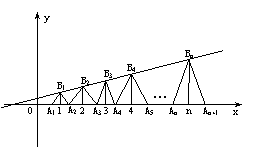22．已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)（n∈N）
顺次为一次函数
图象上的点，
点列A1(x1,0)、A2(x2,0)、…、An(xn,0)（n∈N）
顺次为x轴正半轴上的点，其中x1=a（0＜a＜1），
对于任意n∈N，点An、Bn、An+1构成以
Bn为顶点的等腰三角形。
⑴求{yn}的通项公式，且证明{yn}是等差数列；
⑵试判断xn+2-xn是否为同一常数（不必证明），并求出数列{xn}的通项公式；
⑶在上述等腰三角形AnBnAn+1中，是否存在直角三角形？若有，求出此时a值；若不存在，
请说明理由。
解：
高三数学第一学期第4次月考试卷解答
一、填空（4¢×12=48¢）
1．函数y=的定义域为 (0，10) 。
2．计算：arc cos(cos)= 4p/5（或144°) 。
3．已知集合 A={xx2＜16}，B={xx≥a}，若A∩B=Æ，则实数a的取值范围是 [4，+∞） 。
4．已知a、b、c是锐角三角形ABC中角A、B、C的对边，若b=2，c=3，且△ABC的面积为，
则a=
。
5．（理）展开式中含有常数项，则正整数n的最小值为 3 。
（文）在等差数列{an}中，已知a3=2，则a1+a2+a3+a4+a5= 10 。
6．（理）圆ρ=cosθ-sinθ（ρ＞0，0≤θ＜2π）的圆心的极坐标是
。
（文）在条件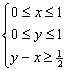 下，使ω=y-2x取得最大值时的点的坐标是 (0，1) 。
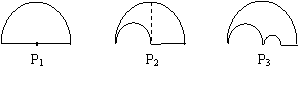7．如图P1是一块半径为1的半圆形纸板，在P1的左下端剪去一个半径为的半圆得图形P2，然后依次剪去一个更小的半圆（其直径为前一个被剪掉半圆的半径），得图形P3、P4、…、Pn、…。记纸板Pn的面积为Sn，则 p/3 。
8．浦东新区二期课改经验交流会打算交流试点学校的论文5篇和非试点学校的论文3篇，排列次序可以任意排列，则最先和最后交流的论文不能来自同类学校的概率是 15/28 。
9．已知xÎC，且，则= -1 。
10．设数列{an}的前n项和为Sn，令Tn=，称Tn为数列a1、a2、…、an的理想数。
已知a1、a2、a3、…、a500的理想数为2004，那么数列6、a1、a2、a3、…、a500的理想数为 2006 。
|
,例如：1*2=1，3*2=2，则函数的值域为
。
12．已知数列，把数列{an}的各项排成如右三角形形状，
记A（(m、n)表示第m行、第n列的项，则A(10、5)=
。
二、选择（4¢×4=16）
13．已知A={yy=}，B={yy=，，则A为 （ C ）
（A）； （B）； （C）[0，]； （D）。
14．若奇函数f(x)在（0，+∞）是增函数，又f(-3)=0，则{x＜0}的解集为 （ B ）
（A）（-3,0）∪（3, +∞）； （B）（-3,0）∪（0,3）；
（C）（-∞,-3）∪（3,+∞）； （D）(-∞,-3)∪（0,3）。
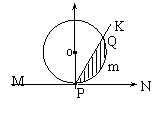15．如图是半径为2的圆，切直线于点P，射线PK从PN出发，
绕P点按逆时钟方向旋转到PM，旋转过程中，PK交圆于
点Q，设OP按逆时钟方向旋转到OQ所形成的角为x，
设弓形PmQ的面积为S=f(x)，那么f(x)的图形大致是 （ D ）
|
16．定义在R上函数f(x)既是偶函数，又是周期函数，若f(x)的最小正周期为π，
当xÎ [0，时，f(x)=sinx，则f()的值为 （ D ）
（A）； （B）-； （C）-； （D）。
三、解答题（12¢+12¢+14¢+14¢+16¢+18¢）
17．已知.
（1）化简
；
（2）若=
，-
，求
；
（3）求出的值域.
解：（1）
Þ
,x¹kp+
,kÎZ (5¢)
（2）
,又-
,∴2x=-
或2x=
Þx=-
或x=
(9¢)
（3）由0＜1-sin2x≤2Þ
≥
Þ的值域为[,+∞) (12¢)
18．已知z为虚数，且2z+15=。
⑴求z；
⑵设u=(3)z，若u在复平面上的对应点在第二、四象限的角平分线上，求复数z；
⑶若z2+2为实数，且z恰好为实系数方程x2+px+q=0的两根，试写出此方程。
解：（1）设z=m+ni(m、nÎR且n¹0)，代入已知式，得 (2m+15)+2ni=
(m+10)+ni
Þ(2m+15)2+4n2=3(m+10)2+3n2Þ4m2+60m+225+n2=3m2+60m+300Þm2+n2=75Þz=5 (4¢)
（2）u=(3-i)(m+ni)=(3m+n)+(3n-m)i,由题设，3m+n+3n-m=0
(6¢),∴
Þ
,或
Þz=2
-i，或z=-2+I (8¢)
（3）
=m2-n2+2mni+2m-2ni=(m2-n2+2m)+2n(m-1)iÎR,且n¹0,∴m=1,又m2+n2=75,
∴
Þ
，∴所求方程为x2-2x+75=0 (12¢)
19．2005年禽流感的爆发，给某疫区禽类养殖户带来了较大的经济损失，某养殖户原来投资共25万，第一个月损失的金额为投资额的，以后由于政府重视，积极防治，疫情趋缓，从第二个月起，每一个月的损失是上月损失的。问：
(1)前三个月中，该养殖户总共损失金额多少万元？
(2)为了维护养殖专业户的利益，政府除了加大防治力度，扑灭疫情之外，还决定给养殖
户一定的经济补偿，该养殖户每月底可向政府领取1.2万元的补偿金，并且每一个月
损失的金额（未补贴前）是上月损失金额的（补贴后）的，问接受了政府补贴后，
该养殖户第3个月损失多少元？又问：与(1)相比较，该养殖户在三个月当中总共可减
少损失多少元？
解：（1）第一个月损失25´=5万元，前3个月的损失费组成首项为5，公比q=的等比数列，
∴S3=
=12.2(万元) (6¢)
（2）第一个月损失5-1.2=3.8万元，第二个月损失3.8´
=1.84万元，第三个月损失
1.84´-1.2=0.272万元，∴第三个月损失了0.227万元. (10¢)
接受补贴后，三个月的损失共为3.8+1.84+0.272=5.912万元，比（1）比较，减少损
失为12.2-5.912=6.288万元 (14¢)
20．已知f(x)=2x+1，将f(x)的反函数y=f—1(x)的图象向上平移1个单位后，再向右平移2个单位，就得到函数y=g(x)的图象。
(1)写出y=g(x)的解析式；
(2)若h(x)，求F(x)=h(x)-g(x)的最值。
解：（1）
(x＞2) (6¢)
（2）
(x＞2). (8¢)(未写范围扣1分)
令u=
≥4´64=96，当x-2=6，即x=8＞2时，上式成立等号，
∴
umin=96 (13¢)，∴
(14¢)
21．⑴证明：当a＞1时，不等式成立。
⑵要使上述不等式成立，能否将条件“a＞1”适当放宽？若能，请放宽条件并简述理由；若不能，也请说明理由。
⑶请你根据⑴、⑵的证明，试写出一个类似的更为一般的结论，且给予证明。
解：（1）证：
,∵a＞1，∴
＞0，
∴原不等式成立 (6¢)
（2）∵a-1与a5-1同号对任何a＞0且a¹1恒成立，∴上述不等式的条件可放宽
为a＞0且a¹1 (9¢)
（3）根据（1）（2）的证明，可推知：若a＞0且a¹1，m＞n＞0，则有
(12¢)
证：左式-右式=
(14¢)
若a＞1，则由m＞n＞0Þam-n＞0,am+n＞0Þ不等式成立；
若0＜a＜1，则由m＞n＞0Þ0＜am-n＜1, 0＜am+n＜1Þ不等式成立.(16¢)
22．已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)（n∈N）
顺次为一次函数图象上的点，
点列A1(x1,0)、A2(x2,0)、…、An(xn,0)（n∈N）
顺次为x轴正半轴上的点，其中x1=a（0＜a＜1），
对于任意n∈N，点An、Bn、An+1构成以
Bn为顶点的等腰三角形。
⑴求{yn}的通项公式，且证明{yn}是等差数列；
⑵试判断xn+2-xn是否为同一常数（不必证明），并求出数列{xn}的通项公式；
⑶在上述等腰三角形AnBnAn+1中，是否存在直角三角形？若有，求出此时a值；若不存在，
请说明理由。
解：（1）
(nÎN),yn+1-yn=
,∴{yn}为等差数列 (4¢)
（2）xn+1-xn=2为常数 (6¢) ∴x1,x3,x5,…,x2n-1及x2,x4,x6,,…，x2n都是公差为2的等差数列，
∴x2n-1=x1+2(n-1)=2n-2+a，x2n=x2+2(n-1)=2-a+2n-2=2n-a，
∴xn=
(10¢)
（3）要使AnBnAn+1为直角三形，则 AnAn+1=2
=2(
)Þxn+1-xn=2()
当n为奇数时，xn+1=n+1-a，xn=n+a-1,∴xn+1-xn=2(1-a).
Þ2(1-a)=2() Þa=
(n为奇数，0＜a＜1)
(*)
取n=1，得a=，取n=3，得a=
，若n≥5，则(*)无解； (14¢)
当偶数时，xn+1=n+a，xn=n-a，∴xn+1-xn=2a.
∴2a=2()Þa=(n为偶数，0＜a＜1)
(*¢)，取n=2，得a=
,
若n≥4，则(*¢)无解.
综上可知，存在直角三形，此时a的值为、、. (18¢)