高三数学第一学期第三次阶段测试
数学试题
一、填空题:本大题共14小题,每小题5分,共70分.答案填在题中横线上
1.已知集合![]() ,
,![]() ,则
,则![]() __ ▲ .
__ ▲ .
2.设![]() 则
则![]() 的值等于__ ▲ .
的值等于__ ▲ .
3.复数![]() 在复平面上对应的点位于第 __ ▲ 象限.
在复平面上对应的点位于第 __ ▲ 象限.
4.在△ABC中,BC=1,![]() ,当△ABC的面积等于
,当△ABC的面积等于![]() 时,
时,![]() __ ▲ .
__ ▲ .
 5.设
5.设![]() 是一次函数,
是一次函数,![]() 且
且![]() 成等比数列, 则
成等比数列, 则![]() …
…![]() __ ▲
__ ▲
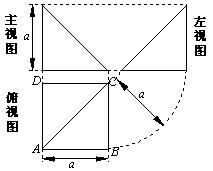
6.四棱锥![]() 的顶点P在底面ABCD中的投影恰好是A,其三视图如右图,则四棱锥
的顶点P在底面ABCD中的投影恰好是A,其三视图如右图,则四棱锥![]() 的表面积为__ ▲
的表面积为__ ▲
7.函数![]()
![]() 的图象恒过定点
的图象恒过定点![]() ,若点
,若点![]() 在一次函数
在一次函数![]() 的图象上,其中
的图象上,其中![]() ,则
,则![]() 的最小值为__ ▲ .
的最小值为__ ▲ .
8.设O是△ABC内部一点,且![]() 的面积之比为__ ▲
的面积之比为__ ▲
9.若函数![]() 是定义在(0,+
是定义在(0,+![]() )上的增函数,且对一切x>0,y>0满足
)上的增函数,且对一切x>0,y>0满足![]() ,则不等式
,则不等式![]() 的解集为__ ▲
的解集为__ ▲
10.(理)若直线![]() 与圆
与圆![]() 交于M、N两点,并且M、N关于直线
交于M、N两点,并且M、N关于直线![]() 对
对
称,则不等式组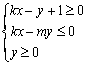 表示的平面区域的面积是__ ▲
表示的平面区域的面积是__ ▲
(文)不等式组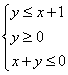 表示的平面区域的面积是__ ▲
表示的平面区域的面积是__ ▲
11.已知函数![]() 的导数
的导数![]() 处取到极大值,则a的取值范围是 ▲
处取到极大值,则a的取值范围是 ▲
12.若从点O所作的两条射线OM、ON上分别有点![]() 、
、![]() 与点
与点![]() 、
、![]() ,则三角形面积之比为:
,则三角形面积之比为: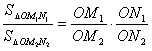 . 若从点O所作的不在同一个平面内的三条射线OP、OQ和OR上分别有点
. 若从点O所作的不在同一个平面内的三条射线OP、OQ和OR上分别有点![]() 、
、![]() 与点
与点![]() 、
、![]() 和
和![]() 、
、![]() ,则类似的结论为:__
▲
,则类似的结论为:__
▲
13.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
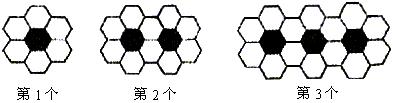
则第n个图案中有白色地面砖__ ▲ 块.
14.给出定义:若![]() (其中
(其中![]() 为整数),则
为整数),则![]() 叫做离实数
叫做离实数![]() 最近的整数,记作
最近的整数,记作![]() ,即
,即 ![]() . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数![]() 的四个命题:
的四个命题:
①函数![]() 的定义域是R,值域是[0,
的定义域是R,值域是[0,![]() ];
];
②函数![]() 的图像关于直线
的图像关于直线![]() (k∈Z)对称;
(k∈Z)对称;
③函数![]() 是周期函数,最小正周期是1;
是周期函数,最小正周期是1;
④ 函数![]() 在
在![]() 上是增函数;
上是增函数;
则其中真命题是__ ▲
二、解答题:本大题共6小题,共90分.解答应写出文字说明,证明过程或演算过程
15.(本小题满分14分) 已知向量![]() =(sinB,1-cosB),且与向量
=(sinB,1-cosB),且与向量![]() (2,0)所成角为
(2,0)所成角为![]() ,其中A, B, C是⊿ABC的内角. (1)求角B的大小; (2)求sinA+sinC的取值范围.
,其中A, B, C是⊿ABC的内角. (1)求角B的大小; (2)求sinA+sinC的取值范围.
16.(本小题满分14分) 已知数列![]() 满足
满足![]()
(Ⅰ)求证:数列![]() 为等差数列;
为等差数列;
(Ⅱ)试问![]() 是否是数列
是否是数列![]() 中的项?如果是,是第几项;如果不是,请说明理由
中的项?如果是,是第几项;如果不是,请说明理由
17.(本小题满分15分) 设有关于![]() 的一元二次方程
的一元二次方程![]() .
.
(Ⅰ)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数,![]() 是从
是从![]() 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率.
(Ⅱ)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数,![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
18.(本小题满分15分)
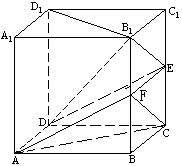
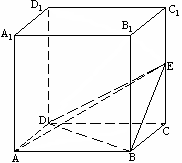
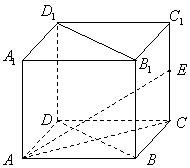 已知:正方体
已知:正方体![]() ,
,![]() ,E为棱
,E为棱![]() 的中点.
的中点.
(Ⅰ) 求证:![]() ;
;
(Ⅱ) 求证:![]() 平面
平面![]() ;
;
(Ⅲ)求三棱锥![]() 的体积
的体积
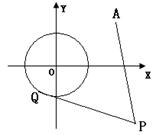 19.(本小题满分16分) (理科做)已知⊙
19.(本小题满分16分) (理科做)已知⊙![]() 由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足
由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足![]()
(1)求实数a,b间满足的等量关系; (2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程。
(文科做)已知二次函数![]() 满足:对任意实数x,都有
满足:对任意实数x,都有![]() ,且当
,且当![]() (1,3)时,有
(1,3)时,有![]() 成立。
成立。
(1)证明:![]() 。
(2)若
。
(2)若![]() 的表达式。
的表达式。
(3)设![]()
![]() ,若
,若![]() 图上的点都位于直线
图上的点都位于直线![]() 的上方,求实数m的取值范围。
的上方,求实数m的取值范围。
20.(本小题满分16分) 已知二次函数![]() 同时满足:①不等式
同时满足:①不等式![]() 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立。设数列
成立。设数列![]() 的前n项和
的前n项和![]() 。
。
(1)求函数![]() 的表达式;
(2)求数列
的表达式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 的整数I的个数称为这个数列
的整数I的个数称为这个数列![]() 的变号数。令
的变号数。令![]() (n为正整数),求数列
(n为正整数),求数列![]() 的变号数
的变号数
高三数学第一学期第三次阶段测试(加试)
(满分40分,答卷时间30分钟)
解答题(共4小题,每小题10分,共40分,解答时应写出文字说明,证明过程或演算步骤)
1. (10分)求由曲线![]() 与
与![]() ,
,![]() ,
,![]() 所围成的平面图形的面积
所围成的平面图形的面积
2. (10分)已知矩阵![]() ,其中
,其中![]() ,若点P(1,1)在矩阵A的变换下得到点P’(0,-3),
,若点P(1,1)在矩阵A的变换下得到点P’(0,-3),
(1)求实数a的值; (2)求矩阵A的特征值及特征向量
3. (10分)某商场举行抽奖促销活动,抽奖规则是:从装有9个白球,1个红球的箱子中每次随机地摸出一个球,记下颜色后放回,摸出一个红球可获得奖金10元;摸出2个红球可获得奖金50元,现有甲,乙两位顾客,规定:甲摸一次,乙摸两次,令x表示甲,乙摸球后获得的奖金总额.
求:(I)x的分布列 (II)x的的数学期望
4. (10分)如图,四面体ABCD中,O、E分别是BD、BC的中点,
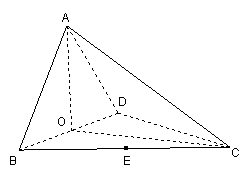
![]()
(I)求证:![]() 平面BCD;
平面BCD;
(II)求点E到平面ACD的距离(用空间向量求解)
高三数学第一学期第三次阶段测试
数学试题必修部分答案
一、填空题:
1. ![]() 2.
2. ![]() 3. 三 4,
3. 三 4,![]() 5,
5,![]() 6,
6,![]() 7,8 8,1
7,8 8,1
9,(0,+![]() ) 10,
) 10,![]() 11,(0,+
11,(0,+![]() ) 12,
) 12,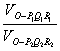
![]() 13,
13,![]()
14,①②③
二、解答题:
15,解:(1)∵![]() =(sinB,1-cosB) , 且与向量
=(sinB,1-cosB) , 且与向量![]() (2,0)所成角为
(2,0)所成角为![]()
∴![]() ………………………3’
………………………3’
∴tan![]() ……………………7’
……………………7’
(2):由(1)可得∴![]() ……10’
……10’
∵![]()
∴![]() ……………………………………………………………………12’
……………………………………………………………………12’
∴![]()
当且仅当![]() …………………………………………14’
…………………………………………14’
16,解:(Ⅰ)当![]() …………2分
…………2分
两边同除以![]() ,…………4分
,…………4分
即![]() 成立,
成立,
∴![]() 为首项,d=4为公差的等差数列. …………7分
为首项,d=4为公差的等差数列. …………7分
(Ⅱ)由(Ⅰ)得,![]() ……9分
……9分
∴![]() …………11分
…………11分
设![]() 是数列
是数列![]() 的第t项,则
的第t项,则![]()
解得,t=11∈N*,………13分
∴![]() 是数列
是数列![]() 的第11项.…………14分
的第11项.…………14分
17. 解:设事件![]() 为“方程
为“方程![]() 有实根”.
有实根”.
当![]() ,
,![]() 时,方程
时,方程![]() 有实根的充要条件为
有实根的充要条件为![]() .
.
(Ⅰ)基本事件共12个:
![]() .其中第一个数表示
.其中第一个数表示![]() 的取值,第二个数表示
的取值,第二个数表示![]() 的取值.
的取值.
事件![]() 中包含9个基本事件,事件
中包含9个基本事件,事件![]() 发生的概率为
发生的概率为![]() .
.
(Ⅱ)试验的全部结束所构成的区域为![]() .
.
构成事件![]() 的区域为
的区域为![]() .
.
所以所求的概率为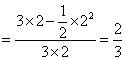 .
.
18. 解:(Ⅰ)证明:连结![]() ,则
,则![]() //
//![]() , …………1分
, …………1分
∵![]() 是正方形,∴
是正方形,∴![]() .∵
.∵![]() 面
面![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() 面
面![]() . ………………4分
. ………………4分
 ∵
∵![]() 面
面![]() ,∴
,∴![]() ,
,
∴![]() . …………………………………………5分
. …………………………………………5分
(Ⅱ)证明:作![]() 的中点F,连结
的中点F,连结![]() .
.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]()
![]()
![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴ ![]() . ………7分
. ………7分
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,∴
,∴![]() .
.
∴四边形![]() 是平行四边形,
是平行四边形,![]() //
//![]() ,
,
 ∵
∵![]() ,
,![]() ,
,
∴平面![]() 面
面![]() . …………………………………9分
. …………………………………9分
又![]() 平面
平面![]() ,∴
,∴![]() 面
面![]() . ………………10分
. ………………10分
(3)![]() . ……………………………12分
. ……………………………12分
![]() 。 ………15分
。 ………15分
19,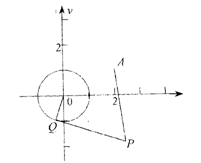 解:(1)连OP,
解:(1)连OP,
![]() 为切点,PQ⊥OQ,由勾股定理有
为切点,PQ⊥OQ,由勾股定理有
![]()
又由已知![]()
即:![]()
化简得实数a、b间满足的等量关系为:
![]() …………………………5分
…………………………5分
(2)由![]() ,得b=-2a+3 。
,得b=-2a+3 。
![]()
![]()
![]()
故当![]() ,即线段PQ长的最小值为
,即线段PQ长的最小值为![]() ………………10分
………………10分
(3)设⊙P的半径为R,
OP设⊙O有公共点,⊙O的半径为1,
![]()
而![]()
![]()
故当![]()
得半径取最小值⊙P的方程为
![]() ……………………16分
……………………16分
本题其它解法参照以上标准酌情给分
(文)解:(1)由条件知 ![]() 恒成立
恒成立
又∵取x=2时,![]() 与恒成立
与恒成立
∴![]() …………4分
…………4分
(2)∵![]() ∴
∴![]() ∴
∴![]() ……6分
……6分
又 ![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
∴![]() , …………10分
, …………10分
解出:![]() ,∴
,∴![]() …………12分
…………12分
(3)由分析条件知道,只要![]() 图象(在y轴右侧)总在直线
图象(在y轴右侧)总在直线 ![]() 上方即可,也就是直线的斜率
上方即可,也就是直线的斜率![]() 小于直线与抛物线相切时的斜率位置,于是:
小于直线与抛物线相切时的斜率位置,于是:
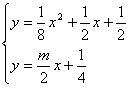 利用相切时△=0,解出
利用相切时△=0,解出 ![]()
∴![]() …………16分
…………16分
解法2:![]() 必须恒成立
必须恒成立
即 ![]() 恒成立
恒成立
①△<0,即 [4(1-m)]2-8<0,解得:![]()
②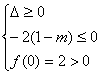 解出:
解出:![]()
总之,![]() ………16分
………16分
20,解(1)![]() 的解集有且只有一个元素,
的解集有且只有一个元素,
![]()
当a=4时,函数![]() 上递减
上递减
故存在![]() ,使得不等式
,使得不等式![]() 成立
成立
当a=0时,函数![]() 上递增
上递增
故不存在![]() ,使得不等式
,使得不等式![]() 成立
成立
综上,得a=4,![]() …………………………5分
…………………………5分
(2)由(1)可知![]()
当n=1时,![]()
当![]() 时,
时,![]()
![]()
![]()
![]() …………………………11分
…………………………11分
(3)由题设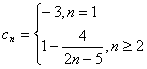 ,
,
![]()
![]()
![]() 递增,
递增,
![]()
即![]() 时,有且只有1个变号数;
时,有且只有1个变号数;
又![]()
∴此处变号数有2个。
综上得数列![]() 的变号数为3。 ………………16分
的变号数为3。 ………………16分
高三数学第一学期第三次阶段测试
数学试题加试部分答案
1.
解:![]()
2.
2. .解:(1)由![]()
![]() =
=![]()
得![]()
(2)由(1)知 ![]()
则矩阵A的特征多项式为
![]()
令![]() ,得矩阵A的特征值为-1或3
,得矩阵A的特征值为-1或3
当![]() 时 二元一次方程
时 二元一次方程![]()
∴矩阵A的属于特征值-1的一个特征向量为![]()
当![]() 时,二元一次方程
时,二元一次方程![]()
∴矩阵A的属于特征值3的一个特征向量为![]()
3. (I) ![]() 取值为0,10,20,50,60.
取值为0,10,20,50,60.
(II) ![]() 元.
元.
4 .解(I)证明:连结OC
![]()
![]()
在![]() 中,由已知可得
中,由已知可得![]()
而![]()
![]()
![]() 即
即![]()
![]()
![]() 平面
平面![]()
(II)解:设平面ACD的法向量为![]() 则
则
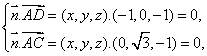
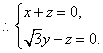
令![]() 得
得![]() 是平面ACD的一个法向量。
是平面ACD的一个法向量。
又![]()
![]() 点E到平面ACD的距离
点E到平面ACD的距离