高三数学第一学期第二次月考卷
一、填空题（本大题共有12个小题，每小题4分，满分共得48分）
1．若
，则r= 。
2. 方程
的解
______.
3．已知集合
，
，则
等于 .
4． 若
=
，则x= 。
5．（理） A、B两点的极坐标分别为A（3，
）、B（2，-
），则A、B两点的距离AB= 。
（文）设x,y满足约束条件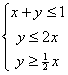
，则目标函数
的最大值是 。
（南校） 
的展开式中的常数项为
.
6．已知函数
，则方程
的解______.
7．把下面不完整的命题补充完整，并使之成为真命题：若函数
的图象
与
的图象关于 对称，则函数= .
8．已知
。
9.对一切实数x，不等式
恒成立，则实数a的取值范围是 。
10. 函数
，使
的取值范围是
。
11．函数
的图象与直线
有且仅有两个不同的交点，则
的取值范围是
。
12．设函数f(x)的图象与直线x=a，x=b及x轴所围成图形的面积称为函数f(x)在[a，b]上的面积，已知函数y＝sinnx在[0，
]上的面积为
（n∈N* ），
那么y＝sin3x在[0,
]上的面积为
，则y＝sin（3x-π）+1在[
，
]上的面积为 。
二、选择题
13. 有甲、乙、丙三项任务，甲需2人，乙、丙各需1人承担，从10人中选派4人承担这三项任务，不同的选法共有 （ ）A．1620种 B．2520种 C．2025种 D．5040种
14．
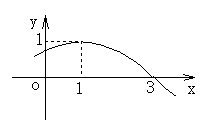函数
（x∈R，
＞0，0≤
＜2
的部分图象如图，则 （ ）
A．＝
，＝
B．＝,＝
C．＝,＝
D．＝,＝
15．设函数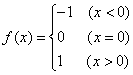
，则当
时，
的值应为（ ）
（A）
； （B）
； （C）
中的较小数； （D）中的较大数。
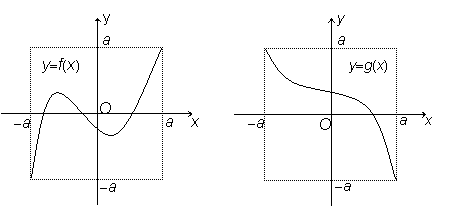
16．定义域和值域均为[-a,a] (常数a>0)的函数y=f(x)和y=g(x)的图像如图所示，
给出下列四个命题中：
(1) 方程f[g(x)]=0有且仅有三个解； (2) 方程g[f(x)]=0有且仅有三个解；
(3) 方程f[f(x)]=0有且仅有九个解； (4)方程g[g(x)]=0有且仅有一个解。
那么，其中正确命题的个数是 ( )
(A) 1； (B) 2； (C) 3； (D) 4。
答题纸
一 、填空（48分）
1.________ , 2.______ _, 3._________ , 4._________ _,
5._________ , 6. _________ , 7._________ , 8.________ ,
9.________ _, 10._________ , 11. , 12.
二、选择（16分）
13._______, 14.___ ____, 15. , 16.
三、解答题
17．已知函数
（
周期为
.
求：当
时
的取值范围.
解：
18．（14分）记函数
的定义域为
，
的定义域为
，
（1）求： （2）若
，求
、
的取值范围。
解：
19. 设函数
，其中
（1）解不等式
（2）求
的取值范围，使
在区间
上是单调减函数。
解：
20．经观测，某公路段在某时段内的车流量（千辆/小时）与汽车的平均速度
（千米/小时）之间有函数关系：
（1）在该时段内，当汽车的平均速度为多少时车流量最大？最大车流量为多少？（精确到
千辆）；
（2）为保证在该时段内车流量知道为10千辆/小时，则汽车的平均速度应控制在什么范围内？
解：
21．(16分已知函数f(
)=sin2－2sincos+3cos2的图象沿轴向左平移m个单位
（m＞0）所得到函数的图象关于直线
对称
①求m的最小值
②证明：当
∈（-
，-
）时，
＜0
③设有不相等的实数，1、2∈（0，
）且f(1)= f(2)=1，求1+2的值
解：
∴
22．（本题满分16分）若函数
对定义域中任一均满足
，则函数
的图像关于点
对称。
（1）已知函数
的图像关于点
对称，求实数
的值；
（2）已知函数在
上的图像关于点
对称，且当
时，
，求函数在
上的解析式；
（3）在（1）、（2）的条件下，若对实数
及
，恒有
，
求实数的取值范围。
解：
2006届川沙中学高三第一学期数学第二次月考卷解答
一、填空题（本大题共有12个小题，每小题4分，满分共得48分）
1．若，则r= 4或6 。
2. 方程的解__2____.
3．已知集合，，则等于
.
4．若=，则x= -
。
5．[理] A、B两点的极坐标分别为A（3，）、B（2，-），则A、B两点的距离AB= 
。
[文] 设
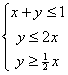满足约束条件，则目标函数的最大值是 5 。
[南校] 的展开式中的常数项为 84 .
6．已知函数，则方程的解___1___.
7．把下面不完整的命题补充完整，并使之成为真命题：若函数的图象
与的图象关于 对称，则函数= .
（注：填上你认为可以成为真命题的一种情形即可，不必考虑所有可能的情形）
(①x轴，
②y轴，
)③原点，
④直线
8．已知__－2__。
9.对一切实数x，不等式恒成立，则实数a的取值范围是[-2，+
) 。
10. 函数，使的取值范围是
或
.
11．函数的图象与直线有且仅有两个不同的交点，则的取值范围是__
_。
12．设函数f(x)的图象与直线x=a，x=b及x轴所围成图形的面积称为函数f(x)在[a，b]上的面积，已知函数y＝sinnx在[0，]上的面积为（n∈N* ），
那么y＝sin3x在[0,]上的面积为，则y＝sin（3x-π）+1在[，]上的面积为 
.
二、选择题
13. 有甲、乙、丙三项任务，甲需2人，乙、丙各需1人承担，从10人中选派4人承担这三项任务，不同的选法共有 （ B ）A．1620种 B．2520种 C．2025种 D．5040种
14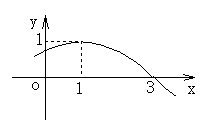．函数（x∈R，＞0，0≤＜2的部分图象如图，则 （ C ）
A．＝，＝
B．＝,＝
C．＝,＝
D．＝,＝
15．设函数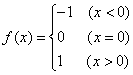，则当时，的值应为（ D ）
（A）； （B）； （C）中的较小数； （D）中的较大数。
16．定义域和值域均为[-a,a] (常数a>0)的函数y=f(x)和y=g(x)的图像如图所示，
给出下列四个命题中：
(1) 方程f[g(x)]=0有且仅有三个解； (2) 方程g[f(x)]=0有且仅有三个解；
(3) 方程f[f(x)]=0有且仅有九个解； (4)方程g[g(x)]=0有且仅有一个解。
那么，其中正确命题的个数是 ( B )
(A) 1； (B) 2； (C) 3； (D) 4。
三、解答题
17．已知函数（周期为.
求：当时的取值范围.
解：
----------------4分（每个公式的应用得2分）
--------------------------2分
因为
，所以
------------------2分
因为
，所以
-----------1分
---------------1分
故 
-------------------------2分
18．（14分）记函数的定义域为，
的定义域为，
（1）求： （2）若，求、的取值范围。
解：（1）
（2）
，由，得
，则
，即
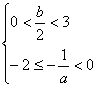
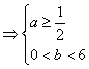
19. 设函数，其中
（1）解不等式 （2）求的取值范围，使在区间上是单调减函数。
解：（1）不等式即为
当
时，不等式解集为
当
时，不等式解集为
当
时，不等式解集为
（2）在上任取
，则
所以要使在递减即
，
只要
即
故当时，在区间上是单调减函数。
20．经观测，某公路段在某时段内的车流量（千辆/小时）与汽车的平均速度（千米/小时）之间有函数关系：
（1）在该时段内，当汽车的平均速度为多少时车流量最大？最大车流量为多少？（精确到千辆）；
（2）为保证在该时段内车流量知道为10千辆/小时，则汽车的平均速度应控制在什么范围内？
解：（1）
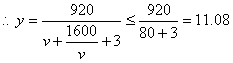， 其中等号成立
当汽车的平均速度为40（千米/小时）时，车流量最大为11.08（千辆/小时）
（2）由题意，
，
为保证车流量至少为10千辆/小时，汽车的速度应控制在25至64千米/小时的范围内。
21．(16分已知函数f()=sin2－2sincos+3cos2的图象沿轴向左平移m个单位
（m＞0）所得到函数的图象关于直线对称
①求m的最小值
②证明：当∈（-，-）时，＜0
③设有不相等的实数，1、2∈（0，）且f(1)= f(2)=1，求1+2的值
解：⑴f()=sin2－2sincos+3cos2=1+2cos2－sin2=
----3’
将f()的图象向左移动m个单位（m＞0）得g()= 
∵ 此时关于=对称：2×+2m+
∴ 2m=
即 m=
(k∈z)
又 ∵ m＞0 ∴ mmin=
--------------6’
⑵ ∵ 
∴
∴f()在（―
，―
）是单调减函数 即1＜2 f(1)＞f(2)---9’
∴ 
＜0 (10分)
⑶ 由f()=1得cos
∴
∴ 
或 
又 ∵ 1、2 
且
∴ 1= 2=
∴
1+2=
--------16分
22．（本题满分16分）
若函数对定义域中任一均满足，则函数的图像关于点对称。
（1）已知函数的图像关于点对称，求实数的值；
（2）已知函数在上的图像关于点对称，且当 时，，求函数在上的解析式；
（3）在（1）、（2）的条件下，若对实数及，恒有，求实数的取值范围。
解：（1）由题设可得
，解得
；……………4分
（2）当时，
； …………………8分
（3）由（1）得
， 其最小值为
，……11分
， ……………………………13分
①当
，即
时，
，得
，15分
②当
，即
时，
，得
，…………17分
由①、②得
。……………………………………………18分