高三年级数学第一学期期终基础学业测评
一、填空题:(本大题共10题,每题4分,满分40分)
1、已知![]() ,且复数
,且复数![]() 的积
的积![]() 是实数,则
是实数,则![]() 的值是__________。
的值是__________。
2、已知![]() ,则
,则![]() 的值是__________。
的值是__________。
3、计算:![]() __________。
__________。
4、已知![]() ,则正整数
,则正整数![]() 的值为__________。
的值为__________。
 5、已知集合
5、已知集合![]() ,
,![]() ,且
,且![]() ,则实数
,则实数![]() 的值是__________。
的值是__________。
6、已知函数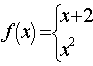
![]() ,若
,若![]() ,则
,则![]() 的值是__________。
的值是__________。
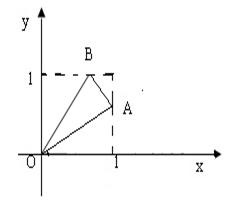
7、如图,在平面直角坐标中有![]() ,其中
,其中![]() 为坐标原点,
为坐标原点,![]() ,当
,当![]() 在
在![]() 内变化时,
内变化时,![]() 面积的最大值为__________。
面积的最大值为__________。
8、从5名学生中选3人参加数学、物理、化学三科竞赛,每科只参加1人,若其中学生甲不能参加化学竞赛,则不同的参赛方案有__________种。
9、在5张卡片上分别写着数字1、2、3、4、5,然后把它们混合再任意排成一行,则得到的五位数能被5或者2整除的概率是__________。(用分数作答)
10、(理)![]() 的展开式中
的展开式中![]() 项的系数是__________。(用数字作答)
项的系数是__________。(用数字作答)
(文)已知![]() 是定义在
是定义在![]() 上的奇函数,又是以3为周期的周期函数,若
上的奇函数,又是以3为周期的周期函数,若![]() ,则
,则![]() 的值是_________。
的值是_________。
二选择题:(本大题共4题,每题4分,共16分)
11、已知![]() 是第二象限角,则
是第二象限角,则![]() 可化简为
可化简为![]() (
)
(
)
![]()
![]()
![]()
![]()
12、已知![]() 、
、![]() 为实数,则
为实数,则![]() 饿充分不必要条件
饿充分不必要条件![]()
![]() ( )
( )
![]()
![]()
![]()
![]()
13、函数![]() 的值域是区间
的值域是区间![]() ,则
,则![]() 与
与![]() 的大小是
的大小是![]() ( )
( )
![]()
![]()
![]()
![]() 无法确定
无法确定
14、已知偶函数![]() 的定义域为
的定义域为![]() ,则正数
,则正数![]() 的值为
的值为![]() ( )
( )
![]()
![]()
![]()
![]()
 三、解答题(本大题共6题,第15、16、17题每题6分,第18、19题每题8分,第20题10分,共44分)
三、解答题(本大题共6题,第15、16、17题每题6分,第18、19题每题8分,第20题10分,共44分)
15.解不等式:![]()
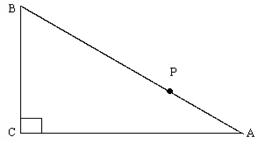
16、已知![]() 中,
中,![]() ,
,![]() 是
是![]() 上动点,求点
上动点,求点![]() 到
到![]() 、
、![]() 的距离乘积的最大值。
的距离乘积的最大值。
17、已知当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
18、已知![]() 是无穷等比数列,且公比
是无穷等比数列,且公比![]() ,它的前
,它的前![]() 项和为
项和为![]() ,计算
,计算![]() 。
。
19、已知数列![]() 的通项公式
的通项公式![]() ,递增的正整数数列
,递增的正整数数列![]() 使
使 ![]() 成等比数列,求数列
成等比数列,求数列![]() 的通项公式。
的通项公式。
20、已知元素为实数的集合![]() 满足下列条件:①1、0
满足下列条件:①1、0![]() ;②若
;②若![]() ,则
,则![]()
![]() 若
若![]() ,求使元素个数最少的集合
,求使元素个数最少的集合![]() ;
;
![]() 在上一小题求得的集合
在上一小题求得的集合![]() 中,任取3个不同元素
中,任取3个不同元素![]() ,求使
,求使![]() 的概率。
的概率。
![]() (本小题选理科的学生做,选文科的学生不做)
(本小题选理科的学生做,选文科的学生不做)
若非空集合![]() 为有限集,则你对集合
为有限集,则你对集合![]() 的元素个数有何猜测?并请证明你的猜测正确。
的元素个数有何猜测?并请证明你的猜测正确。
黄浦区2005学年度第一学期高三年级期终基础学业测评
一、填空题:(本大题共10题,每题4分,满分40分)
1、已知![]() ,且复数
,且复数![]() 的积
的积![]() 是实数,则
是实数,则![]() 的值是____2______。
的值是____2______。
2、已知![]() ,则
,则![]() 的值是____
的值是____ ![]() ______。
______。
3、计算:![]() ____2______。
____2______。
4、已知![]() ,则正整数
,则正整数![]() 的值为______10____。
的值为______10____。
5、已知集合![]() ,
,![]() ,且
,且![]() ,则实数
,则实数![]() 的值是____2______。
的值是____2______。
6、已知函数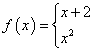
![]() ,若
,若![]() ,则
,则![]() 的值是____
的值是____ ![]() ______。
______。
7、如图,在平面直角坐标中有![]() ,其中
,其中![]() 为坐标原点,
为坐标原点,![]() ,当
,当![]() 在
在![]() 内变化时,
内变化时,![]() 面积的最大值为____
面积的最大值为____ ![]() ______。
______。
8、从5名学生中选3人参加数学、物理、化学三科竞赛,每科只参加1人,若其中学生甲不能参加化学竞赛,则不同的参赛方案有____48______种。
9、在5张卡片上分别写着数字1、2、3、4、5,然后把它们混合再任意排成一行,则得到的五位数能被5或者2整除的概率是____ ![]() ______。(用分数作答)
______。(用分数作答)
10、(理)![]() 的展开式中
的展开式中![]() 项的系数是___165_______。(用数字作答)
项的系数是___165_______。(用数字作答)
(文)已知![]() 是定义在
是定义在![]() 上的奇函数,又是以3为周期的周期函数,若
上的奇函数,又是以3为周期的周期函数,若![]() ,则
,则![]() 的值是___
的值是___ ![]() ______。
______。
二选择题:(本大题共4题,每题4分,共16分)
11、已知![]() 是第二象限角,则
是第二象限角,则![]() 可化简为
可化简为![]() ( B )
( B )
![]()
![]()
![]()
![]()
12、已知![]() 、
、![]() 为实数,则
为实数,则![]() 饿充分不必要条件
饿充分不必要条件![]()
![]() ( C )
( C )
![]()
![]()
![]()
![]()
13、函数![]() 的值域是区间
的值域是区间![]() ,则
,则![]() 与
与![]() 的大小是
的大小是![]() ( A )
( A )
![]()
![]()
![]()
![]() 无法确定
无法确定
14、已知偶函数![]() 的定义域为
的定义域为![]() ,则正数
,则正数![]() 的值为
的值为![]() ( B )
( B )
![]()
![]()
![]()
![]()
三、解答题(本大题共6题,第15、16、17题每题6分,第18、19题每题8分,第20题10分,共44分)
15.解不等式:![]()
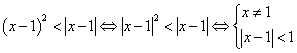
![]() 或
或![]()
另解: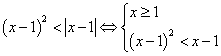 或
或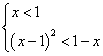
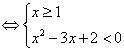 或
或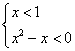
![]() 或
或![]()
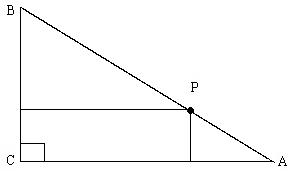 16、已知
16、已知![]() 中,
中,![]() ,
,![]() 是
是![]() 上动点,求点
上动点,求点![]() 到
到![]() 、
、 ![]() 的距离乘积的最大值。
的距离乘积的最大值。
显然![]() ,设
,设![]() ,则点
,则点![]() 到
到![]() 的距离为
的距离为![]() ,点
,点![]() 到
到![]() 的距离为
的距离为![]()
![]() 两距离之积
两距离之积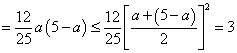
当且仅当![]() 时取到,
时取到,![]() 所求的最大值为3。
所求的最大值为3。
另解:以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴的正半轴建立直角坐标系,
轴的正半轴建立直角坐标系,
则![]() 的方程为
的方程为![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,
,
则点![]() 到
到![]() 的距离分别为
的距离分别为![]()
![]()
当且仅当![]() 时成立,
时成立,![]()
17、已知当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
按题意,![]() 是不等式
是不等式![]() 的解集
的解集![]() 的子集合,
的子集合,
这里![]() 是方程
是方程![]() 的实数根
的实数根![]() ,因此
,因此![]() ,
,![]()
由此推知 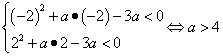
![]() 的取值范围为
的取值范围为![]()
18、已知![]() 是无穷等比数列,且公比
是无穷等比数列,且公比![]() ,它的前
,它的前![]() 项和为
项和为![]() ,计算
,计算![]() 。
。
若![]() ,则
,则![]()
当![]() 时,
时,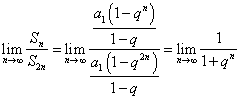
若![]() ,则
,则![]()
若![]() ,则
,则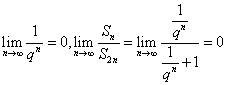
19、已知数列![]() 的通项公式
的通项公式![]() ,递增的正整数数列
,递增的正整数数列![]() 使
使 ![]() 成等比数列,求数列
成等比数列,求数列![]() 的通项公式。
的通项公式。
![]()
![]() 等比数列
等比数列![]() 的公比为
的公比为![]() ,又
,又![]()
故![]()
第一方面![]()
![]()
20、已知元素为实数的集合![]() 满足下列条件:①1、0
满足下列条件:①1、0![]() ;②若
;②若![]() ,则
,则![]()
![]() 若
若![]() ,求使元素个数最少的集合
,求使元素个数最少的集合![]() ;
;
![]() 在上一小题求得的集合
在上一小题求得的集合![]() 中,任取3个不同元素
中,任取3个不同元素![]() ,求使
,求使![]() 的概率。
的概率。
![]() (本小题选理科的学生做,选文科的学生不做)
(本小题选理科的学生做,选文科的学生不做)
若非空集合![]() 为有限集,则你对集合
为有限集,则你对集合![]() 的元素个数有何猜测?并请证明你的猜测正确。
的元素个数有何猜测?并请证明你的猜测正确。
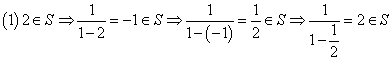 ;
;
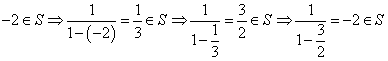
![]() 使
使![]() 的元素个数最少的集合
的元素个数最少的集合![]() 为
为![]()
![]() 设
设![]() 是
是![]() 中三个不同元素,且使
中三个不同元素,且使![]() ,由于
,由于![]() 中仅有2个负数,故只有如下两种可能:
中仅有2个负数,故只有如下两种可能:![]()
![]() 所相对的概率为
所相对的概率为![]()
![]() 非空有限集
非空有限集![]() 的元素个数是3的倍数
的元素个数是3的倍数
证明如下:
设![]() 则
则![]() 且
且
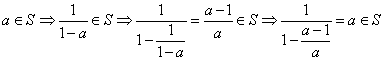
![]()
由于![]() ,但
,但![]() 无实数根
无实数根
故 ![]() 同理
同理![]()
![]()
若存在![]() ,而
,而![]() ,则
,则
![]() 且
且![]()
(若![]() 中有元素
中有元素![]()
![]() ,则利用前述的
,则利用前述的![]() 式可知
式可知![]()
![]() )
)
于是![]()
上述推理还可继续,由于![]() 为有限集,故上述推理有限步可中止
为有限集,故上述推理有限步可中止
![]()
![]() 的元素个数为
的元素个数为![]() 的倍数。
的倍数。