高三年级数学第一学期第三次统一考试
数学试题(文史类)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分.共150分,考试时间120分钟.
第I卷(选择题,共60分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、考号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。
3.考试结束,监考人将本试卷和答题卡一并收回。
参考公式:
如果事件A、B互斥,那么 正棱锥、圆锥的侧面积公式
P(A+B)=P(A)+P(B)
![]()
如果事件A、B相互独立,那么
P(A·B)=P(A)·P(B) 其中c表示底面周长,l表示斜高或母线长
如果事件A在一次试验中发生的概率是 球的体积公式
P,那么n次独立重复试验中恰好发生k
![]()
次的概率![]() 其中R表示球的半径
其中R表示球的半径
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数![]() 是纯虚数,则
是纯虚数,则![]() = ( )
= ( )
A.0 B.1 C.2 D.3
2.抛物线![]() 的焦点到其准线的距离是 ( )
的焦点到其准线的距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
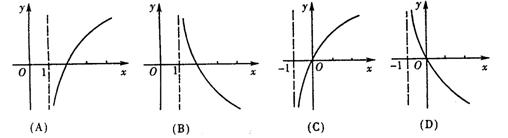
3.用二分法研究函数![]() 的零点时,第一次经计算
的零点时,第一次经计算![]() ,可得其中一个零点
,可得其中一个零点![]() ,第二次应计算 .以上横线上应填的内容为( )
,第二次应计算 .以上横线上应填的内容为( )
A.(0,0.5),![]() B.(0,1),
B.(0,1),![]()
C.(0.5,1),![]() D.(0,0.5),
D.(0,0.5),![]()
|
5.已知a、b表示直线,α、β表示平面,则a∥![]() 的一个充分条件是 ( )
的一个充分条件是 ( )
A.a∥![]() ,
,![]() ∥
∥![]() B.
B. ![]() ⊥
⊥![]() ,a⊥
,a⊥![]()
C.a∥b,b∥![]() D.
D.![]() ,a∥b
,a∥b
6.过抛物线![]() 的焦点,且与圆
的焦点,且与圆![]() 相切的直线方程是 ( )
相切的直线方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
|
A.![]() B.
B.![]()
C.-![]() D.-
D.-![]()
| |
A.5 B.10
C.15 D.20
9.已知函数![]() 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当![]() 时,
时,
![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.2 D.11
C.2 D.11
10.设![]() ,给出下列结论:
,给出下列结论:
①![]() ②
②![]()
③![]() ④
④![]()
其中正确结论的个数是 ( )
A.1个 B.2个 C.3个 D.4个
11.已知等差数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,且A、B、C三点共线(O为该直线外一点),则
,且A、B、C三点共线(O为该直线外一点),则![]() = ( )
= ( )
A.2007 B.![]() C.22007 D.2-2007
C.22007 D.2-2007
12.点P 是双曲线![]() 的右支上一点,M、N分别是圆
的右支上一点,M、N分别是圆![]() =1和圆
=1和圆![]() 上的点,则PM-PN的最大值是 ( )
上的点,则PM-PN的最大值是 ( )
A.2 B.4 C.6 D.8
第II卷(非选择题,共90分)
二、填空题:本大题有4小题,每小题4分,共16分. 把答案填在题中横线上.
 13.某公共汽车站每隔10分钟就有一趟车经过,小王随机赶到车站,则小王等车时间不超过4分钟的概率是 .
13.某公共汽车站每隔10分钟就有一趟车经过,小王随机赶到车站,则小王等车时间不超过4分钟的概率是 .
14.在Rt△ABC中,∠C=90°,∠A=30°,则A、B为
焦点,过点C的椭圆的离心率 .
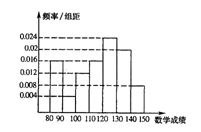
 15.某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中,用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图). 则这10000人中数学成绩在[140,150]段的约是 人.
15.某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试的10000名考生的数学试卷中,用分层抽样的方法抽取500人,并根据这500人的数学成绩画出样本的频率分布直方图(如图). 则这10000人中数学成绩在[140,150]段的约是 人.
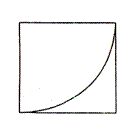
16.一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于 cm3.
| |
三、解答题:本大题有6小题,共74分. 解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
已知数列{![]() }是首项
}是首项![]() 、公比
、公比![]() 的等比数列,
的等比数列,![]() 是其前n项和,且
是其前n项和,且![]() 成等差数列.
成等差数列.
(I)求公比q的值;
(II)求![]() 的值.
的值.
18.(本小题满分12分)
已知函数![]()
(I)求函数![]() 的最小正周期T;
的最小正周期T;
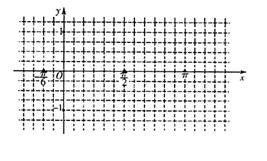
(II)在给定的坐标系中,用“五点法”作出函数![]() 在一个周期上的图象.
在一个周期上的图象.
|
19.(本小题满分12分)
甲乙两人玩一种游戏,每次由甲、乙各出1至5根手指头,若和为偶数算甲赢,否则算乙赢.
(I)若以A表示和为6的事件,求P(A);
(II)现连玩三次,若以B表示甲至少赢一次的事件,C表示乙至少赢两次的事件,试问B与C是否为互斥事件?为什么?
(III)这种游戏规则公平吗?试说明理由.
20.(本小题满分12分)
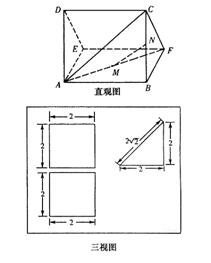
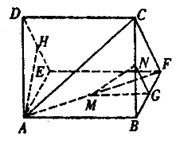
一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点).
(I)求证:MN∥平面CDEF;
|
21.(本小题满分12分)
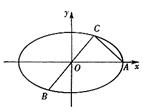
如图,已知A、B、C是椭圆![]() 上的三点,其中点A的坐标为(2
上的三点,其中点A的坐标为(2![]() ,0),BC过椭圆的中心O,且AC⊥BC,BC=2AC.
,0),BC过椭圆的中心O,且AC⊥BC,BC=2AC.
(I)求点C的坐标及椭圆E的方程;
|
22.(本小题满分14分)
已知函数![]() 为常数)是实数集R上的奇函数,函数
为常数)是实数集R上的奇函数,函数![]() 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(I)求a的值;
(II)求λ的取值范围
(III)若![]() 在
在![]() [-1,1]上恒成立,求t的取值范围.
[-1,1]上恒成立,求t的取值范围.
参考答案
一、选择题:本题考查基本知识和基本运算,每小题5分,共60分.
CBADD ACDAA BC
二、填空题:本题考查基本知识和基本运算,每小题4分,共16分.
13.![]() 14.
14.![]() 15.800 16.
15.800 16.![]()
三、解答题: 本大题共6小题,共74分.
17.(本小题满分12分)
解:(I)由已知![]() ,
,![]() ,
,
![]() ,整理得,
,整理得,![]() ………………………………………………3分
………………………………………………3分
解得![]() ,
,
又![]() …………………………………………………………………6分
…………………………………………………………………6分
(II)![]() 构成以
构成以![]() 为首项,以
为首项,以![]() 为公比的等比数列.………………8分
为公比的等比数列.………………8分
![]() ……………………………………………………10分
……………………………………………………10分
![]() …………………………………………12分
…………………………………………12分
18.(本小题满分12分)
解:(I)![]()
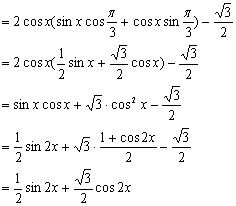
![]() ……………………………………………………4分
……………………………………………………4分
![]() ………………………………………………………………6分
………………………………………………………………6分
(II)列表:
| x |
|
|
|
|
| ||
|
| 0 |
|
|
|
| ||
| sin( | 0 | 1 | 0 | -1 | 0 |
描点画图:
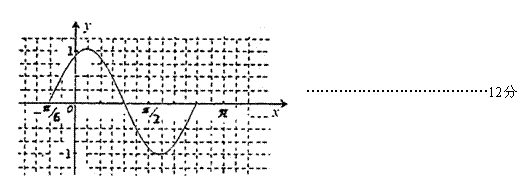 |
19.(本小题满分12分)
解:(I)基本事件空间与点集![]() 中的元素一一对应.
中的元素一一对应.
因为S中点的总数为5×5=25(个),所以基本事件总数为n=25.………………3分
事件A包含的基本事件数共5个;
(1,5)、(2,4)、(3,3)、(4,2)、(5,1)
所以![]() ………………………………………………………………6分
………………………………………………………………6分
(II)B与C不是互斥事件. 因为事件B与C可以同时发生,如甲赢一次,乙赢两次的事件即符合题意.………………………………………………………………………9分
(III)这种游戏规则不公平. 由(I)知和为偶数的基本事件数为13个:
(1,1)、(1,3)、(1,5)、(2,2)、(2,4)、(3,1)、(3,3)、(3,5)、(4,2)、(4,4)、(5,1)、(5,3)、(5,5).
所以甲赢的概率为![]() ,乙赢的概率为
,乙赢的概率为![]() ,
,
所以这种游戏规则不公平.……………………………………………………………12分
|
解:由三视图可知,该多面体是底面为直
角三角形的直三棱住ADE—BCF,……2分
且AB=BC=BF=2,DE=CF=2![]()
∴∠CBF=![]() …………………………4分
…………………………4分
(I)取BF中点G,连MG、NG,由M、N分别为AF、BC
的中点可得,NG∥CF,MG∥EF,………………6分
∴平面MNG∥平面CDEF.
∴MN∥平面CDEF.………………………………8分
(II)取DE的中点H.
∵AD=AE,∴AH⊥DE,在直三棱柱ADE—BCF中,
平面ADE⊥平面CDEF,面ADE∩面CDEF=DE.
∴AH⊥平面CDEF.………………………………………………………………………10分
∴多面体A—CDEF是以AH为高,以矩形CDEF为底面的棱锥,
在△ADE中,AH=![]() ,
,
∴棱锥A—CDEF的体积为![]() …………12分
…………12分
21.(本小题满分12分)
解:(I)∵BC=2AC,且BC经过O(0,0),
∴OC=AC.
又![]() ,
,
![]() ………………………………………………………………………2分
………………………………………………………………………2分
![]() 及C点坐标代入椭圆方程得
及C点坐标代入椭圆方程得![]()
![]() ……………………………………………………5分
……………………………………………………5分
(II)∵PC与CQ所在直线关于直线![]() 对称,
对称,
设直线PC的斜率为k,则直线CQ的斜率为-k,
∴直线PC的方程为![]() ,
,
即![]() ①
①
直线CQ的方程为![]() ②……………………………………7分
②……………………………………7分
将①代入![]() 得
得
![]() ③
③
![]() )在椭圆上,
)在椭圆上, ![]() 是方程③的一个根,
是方程③的一个根,
![]() ……………………………………………………9分
……………………………………………………9分
![]() ,
,
同理可得![]() ,
,
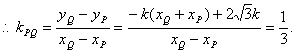 ……………………………………12分
……………………………………12分
22.(本小题满分12分)
解:(I)![]() 是奇函数,
是奇函数,
则![]() 恒成立.
恒成立.
![]()
![]() ……………………4分
……………………4分
(II)![]() 上是减函数,
上是减函数,
![]() 在[-1,1]上恒成立,
在[-1,1]上恒成立,
![]()
![]() …………………………………………………………………………8分
…………………………………………………………………………8分
(III)![]() 在[-1,1]上单调递减,
在[-1,1]上单调递减,![]()
![]()
![]() ………………………………10分
………………………………10分
令![]()
则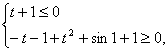 ……………………………………………………12分
……………………………………………………12分
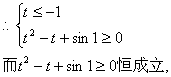
![]() .…………………………………………………………………………14分
.…………………………………………………………………………14分