高三年级数学第一次联合调研考试
试题
注意事项:
1、本试题由必做题与附加题两部分组成,选修历史的考生仅需对试题中的必做题部分做答,考试时间为120分钟；选修物理的考生需对试题中的必做题和附加题这两部分作答,考试时间为150分钟.考试结束后，请将本试卷和答题卡一并交回．
2、答题前，请您务必将自己的学校、班级、姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在试卷及答题卡上规定的地方.
3、作题时必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置，在其它位置作答一律无效.
参考公式：
线性相关系数公式：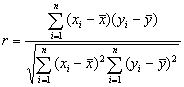
线性回归方程系数公式：
，其中
，
．
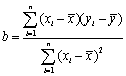必做题部分（满分160分)
一、填空题：本大题共14小题，每小题5分，共计70分．不需写出解答过程，请把答案直接填写在答题卡相应位置上．
1.已知集合
，集合
，则
=
★ .
2．函数
的定义域是 ★
.
3．复数
(
为虚数单位)的实部是 ★ .
4．已知椭圆的中心在原点、焦点在
轴上，若其离心率是
，焦距是8，则该椭圆的方程为 ★ ．
5．在等差数列{
}中，若
，则数列{}前15项的和为 ★ .
6.在
中，如果
∶
∶
=5∶6∶8，那么此三角形最大角的余弦值是 ★ ．
7．若命题“
，使得
”是真命题，则实数
的取值范围是 ★ .
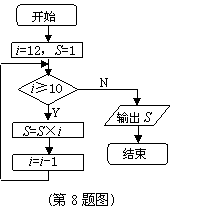8．一个用流程图表示的算法如图所示，则其
运行后输出的结果为 ★ .
9.在一个袋子中装有分别标注数字1,2,3,4,5
的五个小球,这些小球除标注的数字外完全相
同.现从中随机取出两个小球,则取出的小球上
标注的数字之和为5或7的概率是 ★ .
10．若方程
的解为
，则不
小于
的最小整数是 ★ ．
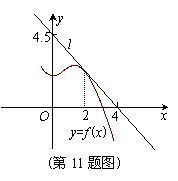
11．如图，函数
的图象在点P处的切线是
，
则
=
★ ．
12.已知如下结论：“等边三角形内任意一点到各边的距
离之和等于此三角形的高”，将此结论拓展到空间中的正
四面体（棱长都相等的三棱锥），可得出的正确结论是：
★ ．
13.若数列
满足
且
,则
★ .
14.已知
是两个互相垂直的单位向量, 且
,
,
,则对任意的正实数
,
的最小值是 ★ .
二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．
15.（本小题满分14分）
已知向量
,
,
,设
.
(Ⅰ)求函数
的最小正周期.
(Ⅱ)若
,且
,求
的值.
16.（本小题满分14分）
如图，在正方体ABCD—A1B1C1D1中，M、N、G
分别是A1A，D1C，AD的中点．求证：
（Ⅰ）MN//平面ABCD；
（Ⅱ）MN⊥平面B1BG．
17.(本小题满分15分)
某电脑公司有6名产品推销员，其工作年限与年推销金额数据如下表:
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限 | 3 | 5 | 6 | 7 | 9 |
| 推销金额 | 2 | 3 | 3 | 4 | 5 |
(Ⅰ)求年推销金额
与工作年限x之间的相关系数；
(Ⅱ)求年推销金额关于工作年限
的线性回归方程；
(Ⅲ)若第6名推销员的工作年限为11年，试估计他的年推销金额.
（参考数据：；由检验水平0.01及
,查表得
.）
18.（本小题满分15分）
已知平面区域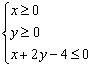
恰好被面积最小的圆
及其内
部所覆盖．
(Ⅰ)试求圆
的方程.
(Ⅱ)若斜率为1的直线
与圆C交于不同两点
满足
,求直线的方程.
19．(本小题满分16分)
已知函数
.
(Ⅰ) 求函数
的单调区间；
(Ⅱ) 当a >0时，求函数在
上最小值.
20．(本小题满分16分)
已知负数a和正数b，令a1=a，b1=b，且对任意的正整数k，当≥0时,有ak+1=ak，
bk+1=；当<0,有ak+1 =，bk+1 = bk．
（1）求bn-an关于n的表达式；
（2）是否存在a,b，使得对任意的正整数n都有bn>bn+1？请说明理由．
（3）若对任意的正整数n，都有b2n-1>b2n，且b2n=b2n+1，求bn的表达式．
附加题部分
（满分40分，时间30分钟）
一、选答题: 本大题共4小题，请从这4题中选做2小题，如果多做，则按所做的前两题记分．每小题10分，共20分.解答时应写出文字说明、证明过程或演算过程．
1．（选修4—1：几何证明选讲）
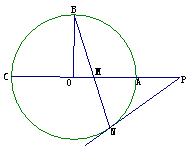如图，
的半径OB垂直于直径AC，M为AO上一点，BM的延长线交于N，过N点的切线交CA的延长线于P．
(1) 求证：
；
（2）若的半径为
，
，求MN的长．
2．（选修4—2：矩阵与变换）
已知矩阵
,向量
.
(Ⅰ)求
的特征值
、
和特征向量
、
；
(Ⅱ)计算
的值.
3．（选修4—4：坐标系与参数方程）
已知曲线
的极坐标方程为
，曲线
的极坐标方程为
，曲线
，
相交于
，
两点.
（Ⅰ）把曲线，的极坐标方程转化为直角坐标方程；
（Ⅱ）求弦
的长度.
4．（选修4—5：不等式选讲）
设
的三边长分别为
，
（1）判定
的符号；
（2）求证：
．
二、必答题: 本大题共2小题，每小题10分，共20分.解答时应写出文字说明、证明过程或演算过程．
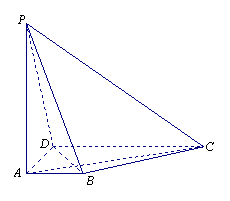
5．如图，在四棱锥
中，底面
为直角梯形，
∥
，
，
⊥平面
，
，
，
.
（Ⅰ）求证：
⊥
；
（Ⅱ）求二面角
的余弦值.
6．在一次电视节目的抢答中，题型为判断题，只有“对”和“错”两种结果，其中某明星判断正确的概率为
，判断错误的概率为
，若判断正确则加1分，判断错误则减1分，现记“该明星答完
题后总得分为
”．
（1）当
时，记
，求
的分布列及数学期望及方差；
（2）当
时，求
的概率．