高三数学上册期末联考
数 学 试 题（文）
命题人：黄冈中学 李新潮 审题人：黄冈中学 王宪生 校对人：黄冈中学 李新潮
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．若
，则a的取值范围是
A．
B．
C．
D．
2．在下列函数中，图象关于直线
对称的是
A．
B．
C．
D．
3．在等差数列
中，
，
，则数列的前9项之和
等于
A．66 B．99 C．144 D．297
4．若
，
，
，
，则
A．
B．
C．
D．
5．下列判断正确的是
A．“正四棱锥的底面是正方形”的逆命题为真命题
B．“
”的充要条件是“
”
C．若“p或q”是真命题，则p、q中至少有一个是真命题
D．不等式
的解集为
6．设椭圆
的左、右焦点分别是
、
，线段
被点
分成
5︰3的两段，则此椭圆的离心率为
A．
B．
C．
D．
7．有一个正方体，六个面上分别写有数字1、2、3、4、5、6，有三个人从不同的角度观察的结果如图所示．如果记3的对面的数字为m，4的对面的数字为n，那么
的值为
A．3 B．7 C．8 D．11
 |
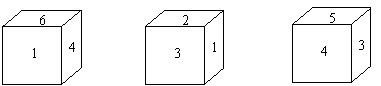8．若
、
是两个不重合的平面，给定以下条件：①、都垂直于平面
；②内不共线的三点到的距离相等；③
、
是内的两条直线，且l∥，m∥；④l、m是两条异面直线，且l∥、l∥、m∥、m∥．其中可以判定∥的是
A．①② B．②③ C．②④ D．④
9．已知平面向量
，
，若
，
，
，则
的值为
A．
B．
C．
D．
10．在△ABC内部有任意三点不共线的2007个点，加上A、B、C三个顶点，共有2010个点，把这2010个点连线，将△ABC分割成互不重叠的小三角形，则小三角形的个数为
A．4017 B．4015 C．4013 D．4012
二、填空题：本大题共5小题，每小题5分，共25分．把答案填在题中横线上．
11．若函数
的反函数为
，则
的值为 ．
12．在△ABC中，
,
，△ABC的周长为
，则x的值为 ．
13．设
，式中的变量x、y满足约束条件
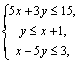则z的最大值为 ．
14．若长方体的三个面的面积分别是
、
、
，则长方体的外接球的体积为
．
15．已知点
在圆
上运动，当角变化时，点运动区域的面积为
．
三、解答题：本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．
16．（本小题满分12分）
已知向量
，
，其中
．记
．
（1）若的最小正周期为
，求函数的单调递增区间；
（2）若函数图象的一条对称轴的方程为
，求
的值．
17．（本小题满分12分）
在△ABC中，∠A、∠B、∠C的对边的边长分别为a、b、c，且
成等比数列．
（1）求角B的取值范围；
（2）若关于角B的不等式
恒成立，求m的取值范围．
18．（本小题满分12分）
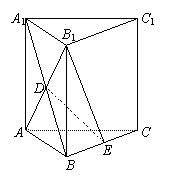在直三棱柱ABC－A1B1C1中，AA1＝AB＝AC＝4，∠BAC＝90°，D为侧面ABB1A1的中心，E为BC的中点．
（1）求证：平面DB1E⊥平面BCC1B1；
（2）求异面直线A1B与B1E所成的角；
（3）求点C1到平面DB1E的距离．
19．（本小题满分12分）
已知二次函数
，
为偶函数，函数的图象与直线
相切．
（1）求的解析式；
（2）若函数
在
上是单调减函数，求k的取值范围．
20．（本小题满分13分）
已知双曲线
的右焦点是F，右顶点是A，虚轴的上端点是B，
，
．
（1）求双曲线的方程；
（2）设Q是双曲线上的一点，且过点F、Q的直线l与y轴交于点M，若
，求直线l的斜率．
21．（本小题满分14分）
已知数列满足
（
，且
），其前n项和
．
（1）求证：为等比数列；
（2）记
，
为数列
的前n项和，那么：
①当
时，求；
②当
时，是否存在正整数m，使得对于任意正整数n都有
？如果存在，求出m的值；如果不存在，请说明理由．
数学（文）参考答案
1．A 2．C 3．B 4．B 5．C 6．D 7．C 8．D 9．B 10．B 11．－1 12．
13．17 14．
15．
16．（1）
．
∵
，∴
，∴
．由
得
．故函数的单调递增区间为
．（8分）
（2）∵直线是函数图象的一条对称轴，∴
，
，得
．又∵，∴令
，得
．（12分）
17．（1）∵
，∴
，当且仅当
时，
，∴
．（5分）
（2）
．
∵
，∴
．
∵不等式恒成立，∴
，得
．
故m的取值范围为
．（12分）
18．（1）连结AE．∵AB＝AC，且E为BC的中点，∴AE⊥BC．∵BB1⊥平面ABC,∴AE⊥BB1，∴AE⊥平面BCC1B1，∴平面DB1E⊥平面BCC1B1．（3分）
（2）延长AB至F，使AB＝BF，连结B1F、EF．在△EBF中，
．
，
．在△EB1F中，
，∴∠EB1F＝
．
∵B1F∥A1B，∴∠EB1F即为异面直线A1B与B1E所成的角．
故异面直线A1B与B1E所成的角为．（8分）
（3）作C1H⊥B1E于H．∵平面DB1E⊥平面BCC1B1，∴C1H⊥平面DB1E，∴C1H的长即为点C1到平面DB1E的距离．∵△B1 H C1∽△B1BE，∴
，∴
．故点C1到平面DB1E的距离为
．（12分）
19．（1）∵为偶函数，∴
，即
恒成立，即
恒成立，
∴
，∴
，∴
．∵函数的图象与直线相切，
∴二次方程
有两相等实数根，∴
，
∴
，
．（6分）
（2）∵
，∴
．∵
在上是单调减函数，∴
在上恒成立，∴
，得
．故k的取值范围为
．（12分）
20．（1）由条件知
，
，
，∴
，代入
中得
，∴
，
．故双曲线的方程为
．（7分）
（2）∵点F的坐标为
，∴可设直线l的方程为
，令
，得
，即
．设
，则由得
，即
，即
∵
，∴
，得
，
．
故直线l的斜率为
．（13分）
21．（1）当
时，
，整理得
，所以是公比为a的等比数列．（4分）
（2）∵，∴
，∴
．
①当时，
，
，两式相减，得
，化简整理，得
．（9分）
②因为
，所以：当n为偶数时，
；当n为奇数时，
．
所以，如果存在满足条件的正整数m，则m一定是偶数．
，其中
．
当时，
，所以
．又因为
，所以：
当
时，
，即
；当
时，
，即
．
故存在正整数
，使得对于任意正整数n都有．（14分）