高三数学上册训练题
班级_____________姓名______________学号_____________成绩__________________
一、 填空题
1、已知函数![]() ,则
,则![]() ________
________
2、设平面![]() 与向量
与向量![]() 垂直,平面
垂直,平面![]() 与向量
与向量![]() 垂直,则平面
垂直,则平面![]() 与
与![]() 位置关系是___________.
位置关系是___________.
3、已知![]() 依次成等比数列,则
依次成等比数列,则![]() 在区间
在区间![]() 内的解集为
.
内的解集为
.
4、椭圆![]() 上到两个焦点距离之积最小的点的坐标是________________.
上到两个焦点距离之积最小的点的坐标是________________.
5、 若函数![]() 的定义域为
的定义域为![]() ,则实数a的取值范围是
.
,则实数a的取值范围是
.
6、设![]() ,则n的值为
.
,则n的值为
.
7、设![]() 、
、![]() 为曲线
为曲线![]() :
:![]() 的焦点,
的焦点,![]() 是曲线
是曲线![]() :
:![]() 与
与![]() 的一个交点,则
的一个交点,则![]() 的值为
.
的值为
.
8、从-3,-2,-1,1,2,3中任取三个不同的数作为椭圆方程![]() 中的系数,则确定不同椭圆的个数为
.
中的系数,则确定不同椭圆的个数为
.
9、
一张报纸,其厚度为![]() ,面积为
,面积为![]() ,现将报纸对折(即沿对边中点连线折叠)7次,这时报纸的厚度和面积分别为_________________。
,现将报纸对折(即沿对边中点连线折叠)7次,这时报纸的厚度和面积分别为_________________。
10、
已知矩形![]() 的边
的边![]() 平面
平面![]() 现有以下五个数据:
现有以下五个数据:
![]() 当在
当在![]() 边上存在点
边上存在点![]() ,使
,使![]() 时,则
时,则![]() 可以取________ _____。(填上一个正确的数据序号即可)
可以取________ _____。(填上一个正确的数据序号即可)
11、某人要买房,随着楼层的升高,上下楼耗费的精力增多,因此不满意度升高,当住在第![]() 层楼时,上下楼造成的不满意度为
层楼时,上下楼造成的不满意度为![]() ,但高处空气清新,噪音较小,因此随楼层升高,环境不满意程度降低,设住在第
,但高处空气清新,噪音较小,因此随楼层升高,环境不满意程度降低,设住在第![]() 层楼时,环境不满意程度为
层楼时,环境不满意程度为![]() ,则此人应选____楼。
,则此人应选____楼。
12、对于任意实数![]() ,符号[
,符号[![]() ]表示
]表示![]() 的整数部分,即[
的整数部分,即[![]() ]是不超过
]是不超过![]() 的最大整数”。在实数轴R(箭头向右)上[
的最大整数”。在实数轴R(箭头向右)上[![]() ]是在点
]是在点![]() 左侧的第一个整数点,当
左侧的第一个整数点,当![]() 是整数时[
是整数时[![]() ]就是
]就是![]() 。这个函数[
。这个函数[![]() ]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。那么
]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。那么![]() =___________________
=___________________
二、选择题
13、已知二面角![]() ,直线
,直线![]() ,
,![]() ,且a与l不垂直,b与l不垂直,那么( )
,且a与l不垂直,b与l不垂直,那么( )
(A)a与b可能垂直,但不可能平行 (B)a与b可能垂直,也可能平行
(C)a与b不可能垂直,但可能平行 (D)a与b不可能垂直,也不可能平行
14、由方程![]() 确定的函数
确定的函数![]() 在
在![]() 上是( )
上是( )
(A) 奇函数 (B) 偶函数 (C) 增函数 (D) 减函数
15、函数![]() ,对任意正数
,对任意正数![]() ,使
,使![]() 成立的一个充分不必要条件是( )
成立的一个充分不必要条件是( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
16、某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:
表1 市场供给量
| 单价 (元/kg) | 2 | 2.4 | 2.8 | 3.2 | 3.6 | 4 |
| 供给量 (1000kg) | 50 | 60 | 70 | 75 | 80 | 90 |
表2 市场需求量
| 单价 (元/kg) | 4 | 3.4 | 2.9 | 2.6 | 2.3 | 2 |
| 需求量 (1000kg) | 50 | 60 | 65 | 70 | 75 | 80 |
根据以上提供的信息,市场供需平衡点(即供给量和需求量相等时的单价)应在区间( )
(A)(2.3,2.6)内 (B)(2.4,2.6)内 (C)(2.6,2.8)内 (D)(2.8,2.9)内
三、解答题
17.若复数![]() 与
与![]() 在复平面上所对应的点关于
在复平面上所对应的点关于![]() 轴对称,且
轴对称,且![]() ,求
,求![]() .
.
18、已知函数![]() ,常数
,常数![]() 。
。
 (1)设
(1)设![]() ,证明:函数
,证明:函数![]() 在
在![]() 上单调递增;
上单调递增;
(2)设![]() 且
且![]() 的定义域和值域都是
的定义域和值域都是![]() ,求
,求![]() 的最大值。
的最大值。
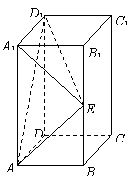
19、长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 是侧棱
是侧棱![]() 的中点.
的中点.
(1)求证:直线![]() 平面
平面![]() ;(本题15分)
;(本题15分)
(2)求三棱锥![]() 的体积;
的体积;
(3)求二面角![]() 的平面角的大小.
的平面角的大小.
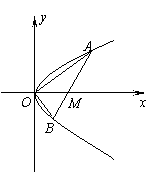
20、如图,直线l与抛物线![]() 交于
交于![]() 两点,与x轴相交于点M,且
两点,与x轴相交于点M,且![]() .
.
(1)求证:M点的坐标为(1,0);
(2)求证:OA⊥OB;
(3)求△AOB的面积的最小值.
21、近几年,上海市为改善城区交通投入巨资,交通状况有了一定的改善,但人民广场仍是市中心交通最为拥堵的地区之一。为确保交通安全,规定在此地段内,车距![]() 是车速
是车速![]() (千米/小时)的平方与车身长
(千米/小时)的平方与车身长![]() (米)之积的正比例函数,且最小车距不得少于车身长的一半,现假定车速为50千米/小时,车距恰为车身长。
(米)之积的正比例函数,且最小车距不得少于车身长的一半,现假定车速为50千米/小时,车距恰为车身长。
⑴ 试写出![]() 关于
关于![]() 的解析式(其中
的解析式(其中![]() 为常数);
为常数);
⑵ 问应规定怎样的车速,才能使此地车流量![]() 最大?
最大?
22、已知数列![]() 中,
中,![]() 且点
且点![]() 在直线
在直线![]() 上.
上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若函数![]() 求函数
求函数
![]() 的最小值;
的最小值;
(3)设![]() 表示数列
表示数列![]() 的前项和。试问:是否存在关于
的前项和。试问:是否存在关于![]() 的整式
的整式![]() ,使得
,使得
![]() 对于一切不小于2的自然数
对于一切不小于2的自然数![]() 恒成立?若存在,写出
恒成立?若存在,写出![]() 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
参考答案
一、 填空题
1、
0; 2、垂直; 3、![]() ; 4、(±5,0); 5、
; 4、(±5,0); 5、![]() ; 6、6;
; 6、6;
7、![]() ; 8、18; 9、
; 8、18; 9、![]() ;
10、①或②; 11、3; 12、8204。
;
10、①或②; 11、3; 12、8204。
二、 选择题
13、B ; 14、D; 15、C ; 16、C。
三、 解答题
17、解:![]() 或
或![]() ,则
,则![]() 或
或![]()
18、解:(1)任取![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,
因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() ,故
,故![]() 在
在![]() 上单调递增。
上单调递增。
(2)因为![]() 在
在![]() 上单调递增,
上单调递增,![]() 的定义域、值域都是
的定义域、值域都是![]()
![]() ,
,
即![]() 是方程
是方程![]() 的两个不等的正根
的两个不等的正根![]() 有两个不等的正根。
有两个不等的正根。
所以![]() ,
,![]()
![]() 。
。
∴![]() ,∴
,∴![]() 时,
时,![]() 取最大值
取最大值![]() 。
。
19、解:(1)依题意:![]() ,
,![]() ,则
,则![]() 平面
平面![]() .
.
(2)![]()
(3)取![]() 的中点
的中点![]() ,连
,连![]() ,则
,则![]() 、
、![]() ,
,
(4)所以![]() 平面
平面![]() .过
.过![]() 在平面
在平面![]()
中作![]() ,交
,交![]() 于
于![]() ,连
,连![]() ,则
,则![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角
的平面角
.在![]() 中,
中,![]()
![]()
20、解:(1 ) 设M点的坐标为(x0, 0), 直线l方程为 x = my + x0 , 代入y2 = x
得
y2-my-x0 = 0 ① y1、y2是此方程的两根,
∴ x0 =-y1y2 =1,即M点的坐标为(1, 0).
(2 ) ∵ y1y2 =-1
∴ x1x2 + y1y2 = y12y22 +y1y2 =y1y2 (y1y2 +1) = 0
∴ OA⊥OB.
(3)由方程①,y1+y2 = m , y1y2 =-1 , 且 OM = x0 =1,
于是S△AOB = ![]() OM y1-y2 =
OM y1-y2 =![]() =
=![]() ≥1,
≥1,
∴ 当m = 0时,△AOB的面积取最小值1.
21、解:⑴ 由已知:![]()
∴ ![]()
当![]() 时,
时,![]()
∴ 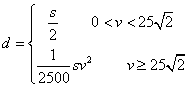
⑵
当![]() 时,
时,![]()
∴ 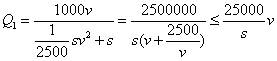 ,此时
,此时![]() 千米/小时
千米/小时
当![]() 时,
时,![]()
∴ 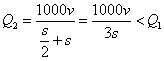
故当![]() 千米/小时时,车流量最大。
千米/小时时,车流量最大。
22、