高三数学上学期第一次质量检测
数 学 试 卷
一、填空题:(每题5分,计70分)
1.函数![]() 的最小正周期为
的最小正周期为
2.已知![]() ,求
,求![]()
3.![]()
4.复数![]() 对应的点位于复平面的第
▲ 象限.
对应的点位于复平面的第
▲ 象限.
5.已知双曲线![]() 垂直,则a=
垂直,则a=
6.已知伪代码如下,则输出结果S= ▲ .
I←0
S←0
While I<6
I←I+2
S←S+I2
End while
Print S
7.若命题“![]() x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
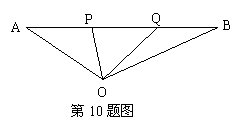 8. 如图,命题:点P,Q是线段AB的三等分点,则有
8. 如图,命题:点P,Q是线段AB的三等分点,则有![]() ,
,
把此命题推广,设点A1,A2 A3,.....,An-1是AB的
n等分点(n![]() 3),则有
3),则有
![]()
![]()
9. 函数![]() 内的交点为P,它们在点P处的两条切线与x轴所围成的三角形的面积为
内的交点为P,它们在点P处的两条切线与x轴所围成的三角形的面积为
10.2008年奥运会8月8日~24日在北京举行,某人为了观看这次体育盛会,从2001年起,每年8月1日到银行存入a元定期储蓄,若年利率为p且保持不变,并约定每年到期本息均自动转存为新的一年定期,到2008年8月1日将所有的存款及利息全部取回(不计利息税),则可取回的钱的总数为 (元)
11.甲、乙两人玩数字游戏,先由甲心中任想一个数字记为![]() ,再由乙猜甲刚才想的数字,把乙想的数字记为
,再由乙猜甲刚才想的数字,把乙想的数字记为![]() ,且
,且![]() ,
,![]() ∈
∈![]() ,若
,若![]() ,则称“甲乙心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________.
,则称“甲乙心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________.
12.某小卖部为了了解热茶销售量y(杯)与气温x(![]() )之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
| 气温( | 18 | 13 | 10 | -1 |
| 杯数 | 24 | 34 | 38 | 64 |
由表中数据算得线性回归方程![]() 中的
中的![]() ,预测当气温为
,预测当气温为![]() 时,热茶销售量为
时,热茶销售量为
____杯.(回归系数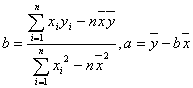 )
)
13.定义在![]() ,且
,且![]() ,若不等式
,若不等式
![]() 对任意
对任意![]() 恒成立,则实数a的取值范围
恒成立,则实数a的取值范围
14.以下四个命题:
①![]()
②函数![]()
③等比数列![]() ;
;
④把函数![]() 的图像向右平移2个单位后得到的图像对应的解析式为
的图像向右平移2个单位后得到的图像对应的解析式为![]()
二、解答题:
15.已知A(3,0),B(0,3),C(![]() .
.
(1) 若![]()
(2) 若![]() 的夹角。
的夹角。
16.高三年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 | 频数 | 频率 |
|
| ① | ② |
|
| 0.050 | |
|
| 0.200 | |
|
| 12 |
|
|
| 0.275 | |
|
| 4 | ③ |
| [145,155] | 0.050 | |
| 合计 | ④ |
(1) 根据上面图表,①②③④处的数值
分别为 ;
(2) 在所给的坐标系中画出[85,155]的频率分布直方图;
(3) 根据题中信息估计总体平均数,并估计总体落在[129,155]中的概率.
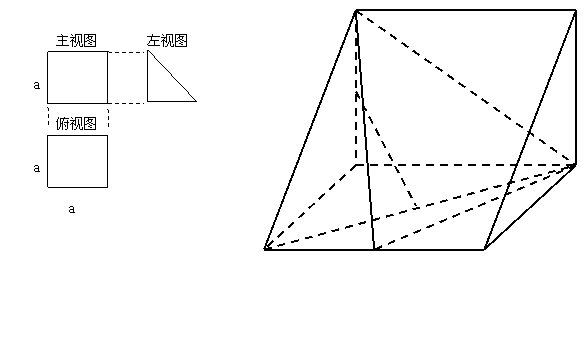
17.一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.(1)求证:![]()
(2)当FG=GD时,在AD上确定一点P,使得GP//平面FMC.


18.若椭圆![]() 过点(-3,2),离心率为
过点(-3,2),离心率为![]() ,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为
,⊙O的圆心为原点,直径为椭圆的短轴,⊙M的方程为![]() ,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
(1)求椭圆的方程;
(2)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的直线方程;
(3)求![]() 的最大值与最小值.
的最大值与最小值.
19.已知二次函数![]() 同时满足:①不等式
同时满足:①不等式![]() 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立。设数列
成立。设数列![]() 的前n项和
的前n项和![]() 。
。
(1)求函数![]() 的表达式;
的表达式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,
,![]() ,数列{
,数列{![]() 的前n项和为
的前n项和为![]() ,
,
若![]() (
(![]() 恒成立,求实数m的取值范围
恒成立,求实数m的取值范围
20.设![]() 、b为函数
、b为函数![]()
(1)求t的取值范围;
(2)判断函数![]() 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)设函数 y=![]() 上的最大值比最小值大
上的最大值比最小值大![]() ,讨论方程f(x)=m解的状况(相同根算一根)。
,讨论方程f(x)=m解的状况(相同根算一根)。
理科加试题
一、必做题(每题10分)
1.盒子中装着有标数字1,2,3,4,5的上卡片各2张,从盒子中任取3张卡片,按3张卡片上最大数字的8倍计分,每张卡片被取出的可能性都相等,用![]() 表示取出的3张卡片上的最大数字,求:
表示取出的3张卡片上的最大数字,求:
(1)取出的3张卡片上的数字互不相同的概率;
(2)随机变量![]() 的概率分布和数学期望;
的概率分布和数学期望;
(3)计分不小于20分的概率.
2.如图所示在直角梯形OABC中![]()
![]()
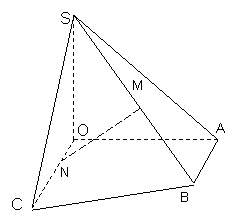 点M是棱SB的中点,N是OC上的点,且ON:NC=1:3,以OC,OA,OS所在直线建立空间直角坐标系
点M是棱SB的中点,N是OC上的点,且ON:NC=1:3,以OC,OA,OS所在直线建立空间直角坐标系![]()
(1) 求异面直线MM与BC所成角的余弦值;
(2) 求MN与面SAB所成的角的正弦值.
二、选做题(从下面4题中选做2题)
3.圆![]() 与椭圆
与椭圆![]() 有公共点,求圆的半径r的取值范围
有公共点,求圆的半径r的取值范围
4.解不等式![]()
5.已知矩阵![]() ,求矩阵M的特征值与特征向量
,求矩阵M的特征值与特征向量
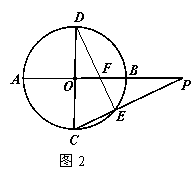
6.如图2所示,![]() 与
与![]() 是⊙O的直径,
是⊙O的直径,![]()
![]()
![]() ,
,![]() 是
是![]() 延长线上一点,连
延长线上一点,连![]() 交⊙O于点
交⊙O于点![]() ,连
,连![]() 交
交![]() 于点
于点![]() ,若
,若![]() .
.
求证:![]()
参考答案:
| 1 |
| 2 |
|
| 3 | 1 | 4 | 一 |
| 5 | 56 | 6 |
|
| 7 | 4 | 8 |
|
| 9 |
| 10 |
|
| 11 | 4/9 | 12 | 70 |
| 13 |
| 14 | ① |
15.已知A(3,0),B(0,3),C(![]() .
.
(3) 若![]()
(4) 若![]() 的夹角。
的夹角。
解:(1)![]() ……………………分
……………………分
![]() ……………………分
……………………分
得![]() ……………………分
……………………分
![]() ……………………分
……………………分
![]() …………………………………………分
…………………………………………分
(2)![]()
![]() ……………………分
……………………分
![]() ……………………分
……………………分
![]()
![]() ……………分
……………分
则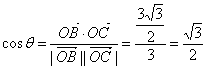 ……………………分
……………………分
![]() 即为所求。……………………分
即为所求。……………………分
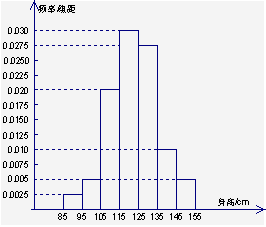
16.解(1) ①1, ②0.025,
③0.1, ④1
(2)直方图如右
(3)利用组中值得
平均数为=90![]() 0.025+100
0.025+100![]() 0.05+110
0.05+110![]() 0.2+120
0.2+120![]() 0.3+130
0.3+130![]() 0.275+140
0.275+140![]() 0.05=122.5 ;
0.05=122.5 ;
在[129,155]上的概率为![]() =
=![]() 0.315
0.315
答:总体平均数约为122.5 在[129,155]上的概率约为0.315
17.证明:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC
(1)连接DB,可知B、N、D共线,且AC⊥DN
又FD⊥AD FD⊥CD,
![]() FD⊥面ABCD
FD⊥面ABCD
![]() FD⊥AC
FD⊥AC
![]() AC⊥面FDN
AC⊥面FDN ![]()
![]() GN⊥AC
GN⊥AC
(2)点P在A点处
证明:取DC中点S,连接AS、GS、GA
![]() G是DF的中点,
G是DF的中点,![]() GS//FC,AS//CM
GS//FC,AS//CM
![]() 面GSA//面FMC
面GSA//面FMC
![]()
![]() GA//面FMC 即GP//面FMC
GA//面FMC 即GP//面FMC
18.解:(1)由题意得: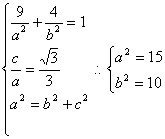
所以椭圆的方程为![]()
(2)由题可知当直线PA过圆M的圆心(8,6)时,弦PQ最大
因为直线PA的斜率一定存在,
设直线PA的方程为:y-6=k(x-8)
又因为PA与圆O相切,所以圆心(0,0)到直线PA的距离为![]()
即![]() 可得
可得![]()
所以直线PA的方程为:![]()
(3)设![]() 则
则![]()
则![]()
![]()
![]()
![]()
19.解(1)![]() 的解集有且只有一个元素,
的解集有且只有一个元素,
![]()
当a=4时,函数![]() 上递减
上递减
故存在![]() ,使得不等式
,使得不等式![]() 成立
成立
当a=0时,函数![]() 上递增
上递增
故不存在![]() ,使得不等式
,使得不等式![]() 成立
成立
综上,得a=4,![]() …………………………5分
…………………………5分
(2)由(1)可知![]()
当n=1时,![]()
当![]() 时,
时,![]()
![]()
![]()
![]() …………………………
…………………………
(3)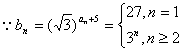 ,
,![]()
![]()
![]()
![]()
![]() ]
]
=![]() 对
对![]() 恒成立,
恒成立,
可转化为:![]() 对
对![]() 恒成立
恒成立
因为![]() 是关于n的增函数,所以当n=2时,其取得最小值18
是关于n的增函数,所以当n=2时,其取得最小值18
所以m<18
20解:(1)![]()
![]() (x>0)
(x>0)
由题意知,![]() 即
即![]() 的两个不等正实根
的两个不等正实根
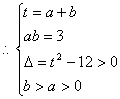 得
得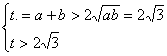
![]()
(2)![]() 单调递增
单调递增
证明![]()
![]()
令![]() ,对称轴为
,对称轴为![]()
又![]()
![]() 恒成立
恒成立
![]() 上单调递增
上单调递增
(3)由(2)可知![]() 单调递增
单调递增
![]()
![]()
![]()
![]()
![]()
消去b可得:![]()
![]()
![]()
![]()
![]()
令![]() 或
或![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
理科加试题
1.盒子中装着有标数字1,2,3,4,5的上卡片各2张,从盒子中任取3张卡片,按3张卡片上最大数字的8倍计分,每张卡片被取出的可能性都相等,用![]() 表示取出的3张卡片上的最大数字,求:
表示取出的3张卡片上的最大数字,求:
(1)取出的3张卡片上的数字互不相同的概率;
(2)随机变量![]() 的概率分布和数学期望;
的概率分布和数学期望;
(3)计分不小于20分的概率.
解:(1)记"一次取出的3张卡片上的数字互不相同的事件"为A,
则![]()
(2)由题意![]() 有可能的取值为:2,3,4,5
有可能的取值为:2,3,4,5
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
所以随机变量![]() 的概率分布为:
的概率分布为:
| | 2 | 3 | 4 | 5 |
| P |
|
|
|
|
所以![]() 的数学期望为E
的数学期望为E![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() +
+![]()
![]() =
=![]()
(3)"一次取出的3张卡片所得分不低于20分"为事件C
![]()
答:
2.如图所示在直角梯形OABC中![]()
![]()
 点M是棱SB的中点,N是OC上的点,且ON:NC=1:3,以OC,OA,OS所在直线建立空间直角坐标系
点M是棱SB的中点,N是OC上的点,且ON:NC=1:3,以OC,OA,OS所在直线建立空间直角坐标系![]()
(3) 求异面直线MM与BC所成角的余弦值;
(4) 求MN与面SAB所成的角的正弦值.
解(1)根据题意可得:
解:如图建系,则S(0,0,1) C(2,0,0) A(0,1,0) B(1,1,0)
所以N (1,0,0) M(![]()
(1) ![]()
![]()
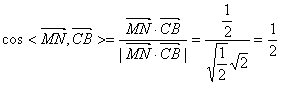
![]()
(2)设平面SAB的一个法向量为![]()
则![]()
![]()
令![]()
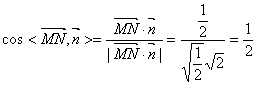
![]()
3.圆![]() 与椭圆
与椭圆![]() 有公共点,求圆的半径r的取值范围
有公共点,求圆的半径r的取值范围
解:将![]() 代入圆方程得
代入圆方程得
![]() =
=![]()
于是![]()
![]()
4.解不等式![]()
解:(Ⅰ)当x<-2时,得-(2x-1)-(x+2)<4得![]() ,此时不等式无解;
,此时不等式无解;
(Ⅱ)当-2![]() x<
x<![]() ,得-(2x-1)+(x+2)<4得x>-1,
,得-(2x-1)+(x+2)<4得x>-1,![]() ;
;
(Ⅲ)当x![]() 时,得(2x-1)+(x+2)<4,得
时,得(2x-1)+(x+2)<4,得![]()
综上原不等式的解集为(-1,1)
5.矩阵变换(本题满分10分)已知矩阵![]() ,求矩阵M的特征值与特征向量
,求矩阵M的特征值与特征向量
解:矩阵M的特征多项式为
![]() …………………分
…………………分
令![]() 得矩阵M特征值为:
得矩阵M特征值为:![]() …………………分
…………………分
将![]() =4代入方程:
=4代入方程:![]()
可得矩阵M属于特征值4的特征向量为![]()
![]() …………………分
…………………分
同理属于特征值-1的特征向量为![]()
![]() …………………分
…………………分
6.如图2所示,![]() 与
与![]() 是⊙O的直径,
是⊙O的直径,![]()
![]()
![]() ,
,![]() 是
是![]() 延长线上一点,连
延长线上一点,连![]() 交⊙O于点
交⊙O于点![]() ,连
,连![]() 交
交![]() 于点
于点![]() ,若
,若![]() .
.
求证:![]()
 证明:
证明:![]()
![]()
![]()
![]()
![]() ∽
∽![]()
![]()
![]()
![]()
![]()
 0.300
0.300