高三数学上学期质量检测

高三数学上学期质量检测

数学试题（文科）

第Ⅰ卷（选择题　共50分）

一、选择题（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的，将正确选项的字母填在答题卡相应的表格中.）

1．设是集合A到集合B的映射，若B={1，2}，则为　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．{1}　　　　　　　　　　 C．或{2}　　　　　　 D．或{1}

2．如果成等比数列，那么　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　 B．　 C．　 D．

3．当下列不等式中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　D．

4．已知等差数列{an}的前n项和为S_n，若且A、B、C三点共线（该直线不过点O），则S₂₀=　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．10　　　　　　　　　　　B．11　　　　　　　　　　　 C．20　　　　　　　　　　　D．21

5．已知函数 的最小值是　　　　　　 （　　）

　　　 A．6　　　　　　　　　　　　B．7　　　　　　　　　　　　C．8　　　　　　　　　　　　D．9

6．已知△ABC的三个内角A、B、C所对的三边分别为a、b、c，若△ABC的面积，则等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．　　　　　　　　　　　D．4

7．已知A、B、C、D是同一球面上的四点，且每两点间距离都等于2，则球心到平面BCD的距离是　　　　　　　　　　（　　）

　　A．　　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　　　　 D．

8．过点M（3，0）的直线交⊙于A、B两点，C为圆心，则 的最小值是　　　　　　　　 　　（　　）

　　　 A．8　　　　　　　　　　　　B．6　　　　　　　　　　　　C．　　　　　　　　　　D．4

9．设双曲线且斜率为1的直线，交双曲线的两渐近线于A、B 两点，若2，则双曲线的离心率为　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　 D．

1,3,5

10．设定义域为R的函数都有反函数，并且函数的图像关于直线的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．1005　　　　　　　　　 B．2008　　　　　　　　　 C．1003　　　　　　　　　 D．以上结果均不对

1,3,5

第Ⅱ卷（非选择题，共100分）

二、填空题（本大题共5小题，每小题5分，共25分，将答案写在答题卡相应的横线上.）

11．△ABC与△DBC所在平面互相垂直，且AB=BC=BD，∠ABC=∠DBC=60°，则二面角A—BD—C的正切值是　　　　　　  .

12．设数列是等差数列，T_n、S_n分别是数列的前n项和，且 则　　　　　　  .

13．给出下列命题：

①函数内单调递增；

②函数的最小正周期为；

③函数的图形是关于直线成轴对称的图形；

④函数的图形是关于点成中心对称的图形.

其中正确命题有　　　　　　  .

14．设F为抛物线A、B、C为该抛物线上三点，若，则=　　　　　　  .

15．已知A（3，），O为原点，点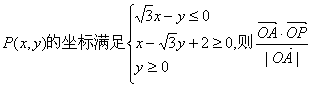的最大值是　　　　　　  ，此时点P的坐标是　　　　　 　 .

三、解答题（本大题共6小题，共75分.解答应写出文字说明、证明过程和演算步骤，将答案写在答题卡相应处.）

16．（本小题满分12分）已知集合

　 （1）求时，求实数a的取值范围；

　 （2）求使的实数a的取值范围。

17．（本小题满分12分）已知平面向量向量

　 （1）求证：；

　 （2）令.

18．（本小题满分12分）如图，平面EAD⊥平面ABCD，△ADE是等边三角形，ABCD是矩形，F、G分别是AB、AD的中点，EC与平在ABCD成30°角。

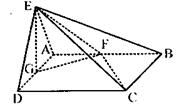
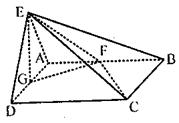
　 （1）求证：CF⊥平面EFG；

　 （2）当AD多长时，点D到平面EFC的距离为2？

19．（本小题满分12分）设数列的各项都是正数，对任意 为数列的前n项和.

　 （1）求数列的通项公式；

　 （2）设，若对任意都有成立，求实数的取值范围。

20．（本小题满分13分）已知A、B、D三点不在一条直线上，且A（－2，0），B（2，0），

　 （1）求点E的轨迹方程；

　 （2）过点A作直线l交以A、B为焦点的椭圆C于M、N两点，线段MN的中点到y轴距离为且直线MN与点E的轨迹相切，求椭圆C的方程。

21．（本小题满分14分）

已知函数

　 （1）求函数的值域；

　 （2）当求函数的最大值；

　 （3）若不等式都恒成立，求实数m的取值范围。

高三数学上学期质量检测

数学试题（文科）参考答案

一、选择题

1—10 DBAAD， BBBCA

1,3,5

二、填空题

11．2　 12．　　13．②④　 14．6　 15．

三、解答题

16．解：（1）若…………2分

∴当的取值范围为…………4分

（2）∵

①当……………………5分

要使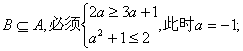………………7分

②当……………………9分

③当

要使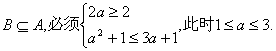………………11分

综上可知，使的实数a的取值范围炎[1，3]…………12分

17．解：（1）∵

∴.……………………2分

　 （2）易知

∵

∴…………………………4分

即

∴

_{……………………6分}

………………9分

∵

∴……………………12分

18．解：（1）∵平面EAD⊥平面ABCD，EG⊥AD，

∴EG⊥平面ABCD，

∴EC与平面ABCD所成角为∠ECG=30°。

设AD=2a，则EG=a，CD=2

∵EG⊥平面ABCD，

∴EG⊥CF。

又∵FG=a，FC=a，CG=3a。

∴CG²=FG²+FC²，

∴CF⊥FG，

故CF⊥平面EFG。…………………………6分

（2）由（1）知CF⊥EF，

∴S_□CEF=

∴当D到平面EFC的距离为2时，V_D—CEF=

又∵S_□DCF=

∴V_E—DCF=

由V_D—CEF=V_E—DCF得

∴AD=时，D到平面EFC的距离为2。……………………12分

19．解：（1）∵由已知，当n=1时，

∴………………………………2分

∵　①

∴当　②

①—②得

∵

∴…………………………4分

因此，数列是首项为1，公差为1的等差数列，故得………………6分

　 （2）要使

即使恒成立。

即恒成立……………………8分

又n=1时，最大值取得－3。……………………10分

∴即实数的取值范围为（3，+）………………12分

20．解：（1）法一：设E

∵

∴

又

∴即为点E的轨迹方程。……………………5分

（法二：可证）

（2）设椭圆方程为：…………6分

由于直线l与圆E相切，

∴

∴

即直线l的方程为：……………………8分

将代入，则有

∴

由题意有……………………11分

又…………13分

21．解：（1）∵易知函数，…………………………1分

且

∴的值域为…………………………3分

（2）设

记…………4分

若

若上单调递减，

若

………………7分

综上知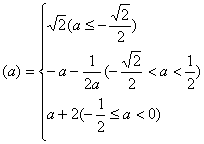………………8分

（3）由（2）知

即恒成立。……………………10分

∴

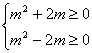
解得

∴实数m的取值范围为………………14分