高三数学下册调研测试
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中仅有一个正确的,请将各题正确答案的序号涂在答题卡的相应位置)
1.
已知![]() ,则
,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.
已知三个力![]() ,
,![]() ,
,![]() ,同时作用于某物体上一点,为使物体保持平衡,需加上一个力
,同时作用于某物体上一点,为使物体保持平衡,需加上一个力![]() ,则
,则![]() 等于.
等于.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 有一块等腰直角三角板ABC,∠C=90°,AB边在桌面上,当三角板所在平面与桌面成45°角时,AC边与桌面所成角的正弦等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.
若过定点![]() 且斜率为
且斜率为![]() 的直线与圆
的直线与圆![]() 在第二象限内的部分有交点则
在第二象限内的部分有交点则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.
已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,若
,若![]() 、
、![]() 、
、![]() 三点共线,(点
三点共线,(点![]() 不在该直线上)则
不在该直线上)则![]()
A.1003 B.
6.
函数![]() 的图象经过适当变换可以得到
的图象经过适当变换可以得到![]() 的图象,则这种变换可以是
的图象,则这种变换可以是
A.沿x轴向右平移![]() 个单位 B.沿x轴向右平移
个单位 B.沿x轴向右平移![]() 个单位
个单位
C.沿x轴向右平移![]() 个单位 D.沿x轴向右平移
个单位 D.沿x轴向右平移![]() 个单位
个单位
7.
下列函数中值域是![]() 的函数是
的函数是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.
已知双曲线![]()
![]() 的离心率
的离心率![]() ,令双曲线两条渐近线构成的角中,以实轴为角平分线的角为
,令双曲线两条渐近线构成的角中,以实轴为角平分线的角为![]() ,则
,则![]() 的取值范围是
的取值范围是
A.[![]() ,
,![]() ]
B.[
]
B.[![]() ,
,![]() ]
C.[
]
C.[![]() ,
,![]() ]
D.[
]
D.[![]() ,
,![]() ]
]
9.
定义:若一条直线垂直于一个平面,则称这条直线的方向向量是这个平面的一个法向量.设向量![]() 是直线
是直线![]() 的方向向量,向量
的方向向量,向量![]() 是平面
是平面![]() 的法向量.下列判断正确的是
的法向量.下列判断正确的是
A.已知![]() ,则
,则![]() ∥
∥![]() 是
是![]() //
//![]() 的充分不必要的条件
的充分不必要的条件
B.已知![]() ⊥
⊥![]() ,则
,则![]() 是
是![]() ⊥
⊥![]() 的必要不充分的条件
的必要不充分的条件
C.已知![]() ⊥
⊥![]() ,则
,则![]() ⊥
⊥![]() 是
是![]() //
//![]() 的充要条件
的充要条件
D.已知![]() ,则
,则![]() ∥
∥![]() 是
是![]() ⊥
⊥![]() 的既不充分又不必要的条件
的既不充分又不必要的条件
10.若锐角△ABC中,若![]() ,
,![]() ,则此三角形最大内角正切的最小值是
,则此三角形最大内角正切的最小值是
A.2 B.3 C.4 D.5
二、填空题(本大题共6小题,每小题5分,共30分.请将各题的正确答案填写在答题卷的相应位置):
11.若![]() 和
和![]() ,
,![]() ,则
,则![]() 的值为 ☆ .
的值为 ☆ .
12.等差数列![]() 中,
中,![]() ,则该数列的前5项的和为 ☆ .
,则该数列的前5项的和为 ☆ .
13.已知![]() 、
、![]() ,则不等式组
,则不等式组![]()
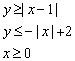 所表示的平面区域的面积是 ☆ .
所表示的平面区域的面积是 ☆ .
14.若函数![]()
![]()
![]() ,则满足
,则满足![]() 的
的![]() 的范围是 ☆ .
的范围是 ☆ .
15.底面半径为2的一个圆锥有三条母线两两垂直,则它的侧面积为 ☆ .
16.已知![]()
![]() ,且方程
,且方程![]() 无实数根,下列命题:
无实数根,下列命题:
①若![]() ,则不等式
,则不等式![]() 对一切实数
对一切实数![]() 都成立;
都成立;
②若![]() ,则必存在实数
,则必存在实数![]() ,使
,使![]() 成立;
成立;
③若![]() ,则不等式
,则不等式![]() 对一切实数
对一切实数![]() 都成立;
都成立;
④方程![]() 一定没有实数根.
一定没有实数根.
中,正确命题的序号是 ☆ (把你认为是正确的命题的所有序号都填上).
三、解答题(本大题共5小题,满分70分.请在答题卷的相应位置解答):
17. (本小题12分)
已知向量![]() ,
,![]()
![]() ,设函数
,设函数![]() 且
且![]() 为偶函数.
为偶函数.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试用五点法作函数![]()
![]() 的图象.
的图象.
18. (本小题14分)
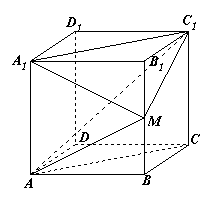
正方体![]() 中,M是棱
中,M是棱![]() 的中点.
的中点.
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的一个三角函数值;
所成角的一个三角函数值;
(Ⅲ)求二面角![]() 的一个三角函数值.
的一个三角函数值.
19. (本小题14分)
从原点出发的某质点![]() ,按照向量
,按照向量![]() 移动的概率为
移动的概率为![]() ,按照向量
,按照向量![]() 移动的概率为
移动的概率为![]() ,设可到达点
,设可到达点![]() 的概率为
的概率为![]() .
.
(Ⅰ)求概率![]() 、
、![]() ;
;
(Ⅱ)求![]() 与
与![]() 、
、![]() 的关系并证明数列
的关系并证明数列![]() 是等比数列;
是等比数列;
(Ⅲ)求![]() .
.
20. (本小题14分)
直线![]() :
:![]() 与
与![]() 轴正方向、
轴正方向、![]() 轴正方向相交于A、B,M、N是直线
轴正方向相交于A、B,M、N是直线![]() 上的点,且
上的点,且![]() ,以坐标轴为对称轴的椭圆C过点M、N.
,以坐标轴为对称轴的椭圆C过点M、N.
(Ⅰ)若直线![]() 是
是![]() ,求椭圆C的方程;
,求椭圆C的方程;
(Ⅱ)若椭圆C的离心率是![]() ,且
,且![]() ,求直线
,求直线![]() 斜率
斜率![]() 的取值范围.
的取值范围.
21. (本小题16分)
设函数![]()
![]() 的图象与直线
的图象与直线![]() 相切于
相切于![]() .
.
(Ⅰ)求![]() 在区间
在区间![]() 上的最大值与最小值;
上的最大值与最小值;
(Ⅱ)是否存在两个不等正数![]()
![]() ,当
,当![]() 时,函数
时,函数![]() 的值域也是
的值域也是![]() ,若存在,求出所有这样的正数
,若存在,求出所有这样的正数![]() ;若不存在,请说明理由;
;若不存在,请说明理由;
(Ⅲ)设存在两个不等正数![]()
![]() ,当
,当![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,求正数
,求正数![]() 的取值范围.
的取值范围.
参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | D | A | A | B | C | D | C | B | B |
11.![]() 12.25 13.
12.25 13.![]() 14.
14.![]() 15.
15.![]() 16.①③④
16.①③④
17.(Ⅰ)![]() ;
;
(Ⅱ)![]()
![]()
![]()
![]()
![]()
18.解一:(Ⅰ)取连![]() 与
与![]() 相交于O,可证MO⊥
相交于O,可证MO⊥![]() ,MO⊥
,MO⊥![]() ,
,
得MO⊥平面![]() ,得平面
,得平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)过![]() 作
作![]() 垂直于
垂直于![]() ,交
,交![]() 于P,连PM。
于P,连PM。
由(Ⅰ)知,![]() ⊥平面
⊥平面![]() ,故
,故![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角,
所成角,
它的正弦值是![]() 。
。
设正方形边长为1,则![]() ,
,![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角正弦值是
所成角正弦值是![]() ;
;
(Ⅲ)同(Ⅱ),过P作![]() 垂直于
垂直于![]() ,连
,连![]() ,知
,知![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成角,它的正切值是
所成角,它的正切值是![]() ;
;
在△![]() 中,同(Ⅱ),设正方体棱长为1,则有
中,同(Ⅱ),设正方体棱长为1,则有
![]() ,
,
所以二面角![]() 的正切值是
的正切值是![]() ;
;

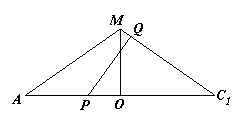
解二:以D为坐标原点,建立如图所示空间直角坐标系,并设正方体棱长为2,则有:
(Ⅰ)平面![]() 的一个法向量是
的一个法向量是![]() ,
,
平面![]() 的一个法向量是
的一个法向量是![]() ,
,
由![]() 知,平面
知,平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)直线![]() 的一个方向向量是
的一个方向向量是![]() ,
,
平面![]() 的一个法向量是
的一个法向量是![]() ,
,
由![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角正弦值是
所成角正弦值是![]() ;
;
(Ⅲ)平面![]() 的一个法向量是
的一个法向量是![]() ,
,
平面![]() 的一个法向量是
的一个法向量是![]() ,
,
由![]() ,
,
所以二面角![]() 的余弦值是
的余弦值是![]() 。
。
19.解 (Ⅰ)![]() 点到达点
点到达点![]() 的概率为
的概率为![]() ;
;![]() 点到达点
点到达点![]() 的事件由两个互斥事件组成:①A=“
的事件由两个互斥事件组成:①A=“![]() 点先按向量
点先按向量![]() 到达点
到达点![]() ,再按向量
,再按向量![]() 到达点
到达点![]() ”,此时
”,此时![]() ;
;
②B=“![]() 点先按向量
点先按向量![]() 移动直接到达点
移动直接到达点![]() ”,此时
”,此时![]() 。
。
![]()
![]()
![]()
![]()
![]()
![]()
(Ⅱ) ![]() 点到达点
点到达点![]() 的事件由两个互斥事件组成:
的事件由两个互斥事件组成:
①![]() “从点
“从点![]() 按向量
按向量![]() 移动到达点
移动到达点![]() ”,
”,
此时![]() ;
;
②![]() “从点
“从点![]() 按向量
按向量![]() 移动到达点
移动到达点![]() ”,此时
”,此时![]() 。
。
![]() ,即
,即 ![]()
![]()
![]() 数列
数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列。
的等比数列。
(Ⅲ)由(Ⅱ)可知![]()
![]()
![]()
![]()
![]()
![]()
……
![]()
![]()
![]()
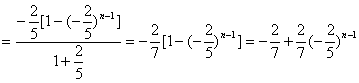
![]()
20.解:(Ⅰ)依题意![]() ,
,![]() ,又
,又![]() ,
,
故![]() ,
,![]() ,设椭圆方程是
,设椭圆方程是![]() ,则
,则
![]() ,解得
,解得![]()
![]() ,故所求椭圆方程是
,故所求椭圆方程是![]() 。
。
(Ⅱ)依题意![]() ,
,![]() ,且
,且![]() ,
,![]() ,又
,又![]() ,
,
故![]() ,
,![]() ,设椭圆方程是
,设椭圆方程是![]() ,则
,则
![]()
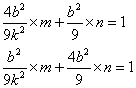 ,解得
,解得![]()
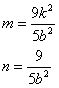 ,故所求椭圆方程是
,故所求椭圆方程是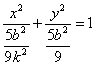 。
。
(1)若![]() ,即
,即![]() ,椭圆的焦点在
,椭圆的焦点在![]() 轴上,此时有:
轴上,此时有:
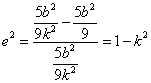 ,由
,由![]() 知,
知,![]() ;
;![]()
(2)若![]() ,即
,即![]() ,椭圆的焦点在
,椭圆的焦点在![]() 轴上,此时有:
轴上,此时有:
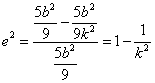 ,由
,由![]() 知,
知,![]() ;
;
综合上可得,当![]() 时,
时,![]() 。
。
21.解:(Ⅰ)![]() 。依题意则有:
。依题意则有:
![]() ,所以
,所以![]() ,解得
,解得![]() ,所以
,所以![]() ;
;
![]() ,由
,由![]() 可得
可得![]() 或
或![]() 。
。
![]() 在区间
在区间![]() 上的变化情况为:
上的变化情况为:
|
| 0 |
| 1 |
| 3 |
| 4 |
|
| + | 0 | — | 0 | + | ||
|
| 0 | 增函数 | 4 | 减函数 | 0 | 增函数 | 4 |
所以函数![]() 在区间
在区间![]() 上的最大值是4,最小值是0。
上的最大值是4,最小值是0。
(Ⅱ)由函数的定义域是正数知,![]() ,故极值点
,故极值点![]() 不在区间
不在区间![]() 上;
上;
(1)若极值点![]() 在区间
在区间![]() ,此时
,此时![]() ,在此区间上
,在此区间上![]() 的最大值是4,不可能等于
的最大值是4,不可能等于![]() ;故在区间
;故在区间![]() 上没有极值点;
上没有极值点;
(2)若![]() 在
在![]() 上单调增,即
上单调增,即![]() 或
或![]() ,
,
则![]() ,即
,即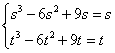 ,解得
,解得![]() 不合要求;
不合要求;
(3)若![]() 在
在![]() 上单调减,即
上单调减,即![]() ,则
,则![]() ,
,
两式相减并除![]() 得:
得:![]() ,
①
,
①
两式相除并开方可得![]() ,
,
即![]() ,整理并除以
,整理并除以![]() 得:
得:![]() ,
②
,
②
则①、②可得![]() ,即
,即![]() 是方程
是方程![]() 的两根,
的两根,
即存在![]() ,
,![]() 满足要求;
满足要求;
(Ⅲ)同(Ⅱ),极值点![]() 不可能在区间
不可能在区间![]() 上;
上;
(1)若极值点![]() 在区间
在区间![]() ,此时
,此时![]() ,
,
故有①![]()
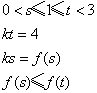 或②
或②![]()
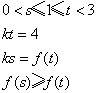
①由![]() ,
,![]() 知,
知,![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ;
;
再由![]() ,
,![]() 知,
知,![]() ,当且仅当
,当且仅当![]() 时,
时,![]()
由于![]() ,故不存在满足要求的
,故不存在满足要求的![]() 值。
值。
②由![]() ,及
,及![]() 可解得
可解得![]() ,
,
所以![]() ,
,![]() 知,
知,![]() ;
;
即当![]() 时,存在
时,存在![]() ,
,![]() ,
,
且![]() ,满足要求。
,满足要求。
(2)若函数![]() 在区间
在区间![]() 单调递增,则
单调递增,则![]() 或
或![]() ,
,
且![]() ,故
,故![]() 是方程
是方程![]() 的两根,
的两根,
由于此方程两根之和为3,故![]() 不可能同在一个单调增区间;
不可能同在一个单调增区间;
(3)若函数![]() 在区间
在区间![]() 单调递减,即
单调递减,即![]() ,
,![]() ,
,
两式相除并整理得![]() ,
,
由![]() 知
知![]() ,即
,即![]() ,
,
再将两式相减并除以![]() 得,
得,
![]()
![]()
![]() ,
,
即![]() 。
。
即![]() ,
,![]() 是方程
是方程![]() 的两根,
的两根,
即存在![]() ,
,![]() 满足要求。
满足要求。
综上可得,当![]() 时,存在两个不等正数
时,存在两个不等正数![]()
![]() ,使
,使![]() 时,函数
时,函数![]() 的值域恰好是
的值域恰好是![]() 。
。