山东省济南市2007年4月高三统一考试
数学(文史类)
第Ⅰ卷(选择题 共60分)
一、 选择题
1、复数![]() 的虚部是
的虚部是
A、2 B、-2 C、2i D、![]()
2、设全集U=R,A={x![]() },则
},则![]() =
=
A、![]() B、
B、 ![]() C、
C、![]() D、
D、![]()
3、已知函数f(x)= ![]() 的定义域和值域都是[0,1],则a 的值是
的定义域和值域都是[0,1],则a 的值是
A、![]() B、 2
C、
B、 2
C、![]() D、
D、![]()
4、如图所示,甲、乙、丙是三个几何体的三视图,甲、乙、丙对应的标号正确的是
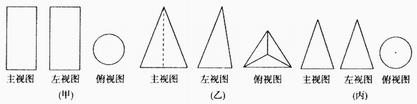
①长方体 ②圆锥 ③三棱锥 ④圆柱
A、④③② B、①③② C、①②③ D、④②③
5、已知![]() ,则
,则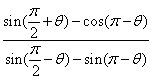 =
=
A、2
B、-2 C、0
D、![]()
6、如图:M是半径为R的圆周上一个定点,在圆周上等可能的任取一点N,连接MN,则弦MN的长度超过![]() 的概率是
的概率是
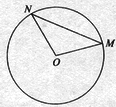
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7、在四边形ABCD中,![]() =(1,2),
=(1,2),![]() =(-4,-1),
=(-4,-1),![]() =(-5,-3),则四边形ABCD的形状是
=(-5,-3),则四边形ABCD的形状是
A、长方形 B、梯形 C、平行四边形 D、以上都不对
8、幂函数![]() 及直线y=x,y=1,x=1将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数
及直线y=x,y=1,x=1将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数![]() 的图象经过的“卦限”是
的图象经过的“卦限”是
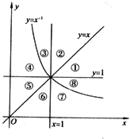
A、⑧,③ B、⑦,③ C、⑥,① D、⑤,①
9、已知:![]() ,则
,则![]() 的值是
的值是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、由等式![]() ,定义一个映射,
,定义一个映射,![]() ,则f(2,1,-1)等于
,则f(2,1,-1)等于
A、(-1,0,-1) B、(-1,-1,0) C、(-1,0,1) D、(-1,1,0)
11、四面体的六条棱中,有五条棱长都等于a,则该四面体的体积的最大值
A 、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、设两条直线的方程分别为x+y+a=0,x+y+b=0,已知a、b是方程的两个实根,且,则这量条直线之间的距离的最大值和最小值分别是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
第Ⅱ卷
二、填空题:本大题共4个小题,每小题4分;共16分.把答案填在题中横线上
13.给出下列命题:
①命题“![]() 使x-1>0”的否定是“对,都有x-1<0” ;
使x-1>0”的否定是“对,都有x-1<0” ;
②卡方独立性检验显示“患慢性气管炎和吸烟习惯有关”,这就是指“有吸烟习惯的人必定会患慢性气管炎”;
③函数f(x)=xx+px+q(![]() )为奇函数的充要条件是q=0.
)为奇函数的充要条件是q=0.
其中错误命题的序号是___________;(将所有错误命题的序号都填上);
14.某地区要对编号00001-100000的学生进行一项调查,拟采用系统抽样的方法抽取一个样本,若样本中学生的编号由关系式![]() 给出,则集合A=___________.
给出,则集合A=___________.
15.已知函数:y=x+3,右面程序框图表示的是给出x值,求所对应的值的算法,请将该程序框图补充完整,其中①处应填 ; ②处应填_______。
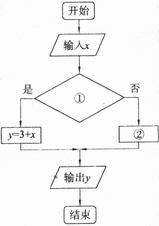
16.在![]() 中,角A、B、C所对的边分别为a、b、c,且
中,角A、B、C所对的边分别为a、b、c,且![]() ,若
,若![]() ,bc的最大值是
,bc的最大值是
三、解答题:本大题共6个小题,共74分.解答应写出文字说明,证明过程或演算步骤
17.(本小题满分12分)
设函数f(x)= ![]() ,
,
(1) 求f(x)的单调区间;
(2)若当x![]() [-2,2]时,不等式f(x)>m恒成立,求实数m的取值范围。
[-2,2]时,不等式f(x)>m恒成立,求实数m的取值范围。
18.(本小题满分12分)
如图,四棱锥P-ABCD中,PA![]() 平面ABCD,PA=AB,底面ABCD为直角梯形,
平面ABCD,PA=AB,底面ABCD为直角梯形,![]()
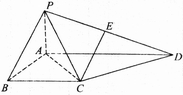
(1)
求证:平面PAC![]() 平面PCD;
平面PCD;
(2) 在棱PD上是否存在一点E,使CE//平面PAB?若存在,请确定E点的位置,若不存在,请说明理由。
19.(本小题满分12分)
已知等差数列{![]() },公差d大于0,且
},公差d大于0,且![]() 是方程
是方程![]() 的两个根,数列{
的两个根,数列{![]() }的前n项和为
}的前n项和为![]() 且
且![]() .
.
(1)求数列{![]() }的前项和
}的前项和![]() ;
;
(2)求{![]() }的通项公式.
}的通项公式.
20.(本小题满分12分)
已知双曲线![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() .
.
(1)求双曲线上满足的点P的坐标;
(2)椭圆![]() 的左、右顶点分别是双曲线
的左、右顶点分别是双曲线![]() 的左、右焦点,椭圆
的左、右焦点,椭圆![]() 的左、右焦点分别是双曲线
的左、右焦点分别是双曲线![]() 的左、右顶点,若直线
的左、右顶点,若直线![]() 与椭圆恒有两个不同的交点A和B,且
与椭圆恒有两个不同的交点A和B,且![]() (其中O为坐标原点),求k的取值范围.
(其中O为坐标原点),求k的取值范围.
21.(本小题满分)2分)
设f(x)= ![]()
(1)讨论函数y=f(x)的单调区间;
(2)P是函数y=f(x)图像上任一点,O为原点;当OP取最小值时,求证:过点P的切线与OP垂直.
22.(本小题满分14分)
己知椭圆![]() 的中心在坐标原点O,焦点在x轴上,离心率为
的中心在坐标原点O,焦点在x轴上,离心率为![]() ,P为椭圆上一动点,
,P为椭圆上一动点,![]() 、
、![]() 分别为椭圆的左、右焦点,且
分别为椭圆的左、右焦点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆短轴的上端点为A,M为动点,且![]() 成等差数列,求动点M的轨迹
成等差数列,求动点M的轨迹![]() 的方程;
的方程;
(3)过点M作![]() 的切线
的切线![]() 交
交![]() 与Q、R两点,求证:
与Q、R两点,求证:![]() .
.
山东省济南市2007年4月高三统一考试
数学(文史类)试题参考答案及评分标准
一、1. A 2. C 3.B 4.A 5.B 6.D 7.B 8.D 9.C 10.A 11.C 12.D
二、13.①② 14.![]()
15.①![]() 或(x>-3);②y=-x-3 16.
或(x>-3);②y=-x-3 16.![]()
三、17.解:(1) ![]() ,…2分
,…2分
设![]() 为f(x)的增区间,
为f(x)的增区间,
![]() 为f(x)的减区间 ……6分
为f(x)的减区间 ……6分
(2)
令:![]() =0,
=0,
![]() x=0和x=-2为极值点,
…8分
x=0和x=-2为极值点,
…8分
![]() …11分
…11分
![]() …12分
…12分
18.解:PA=1.
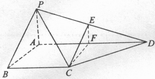
(1) 由题意PA=BC=1,AD=2……2分
AB=1,BC=![]() AD 由
AD 由![]() 易得CD=AC=
易得CD=AC=![]()
由勾股定理逆定理得![]() ……3分
……3分
又PA![]() 面ABCD CD
面ABCD CD![]() 面ABCD
面ABCD
![]() 面PAC,……5分
面PAC,……5分
又CD![]() 面PCD,
面PCD,![]() 面PAC
面PAC ![]() 面PCD
……6分
面PCD
……6分
(2)证明:作CF//AB交AD于F,作EF//AP交PD于E,连接CE……8分
CF//AB EF//PA CF![]() EF=F PA
EF=F PA![]() AB=A
AB=A
平面EFC//平面PAB, ……10分
又CE在平面EFC内,CE//平面PAB BC=![]() AD AF=BC
AD AF=BC
![]() F为AD的中点,
F为AD的中点,![]() E为PD中点
E为PD中点
故棱PD上存在点E,且E为PD中点,使CE//面PAB……12分
19.解:(1)设![]() 的公差为d,由题意得:
的公差为d,由题意得:
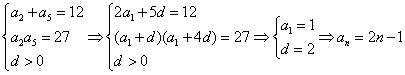 ……4分
……4分
![]() ……6分
……6分
(2) 由![]() 得
得![]() 两式相减得:
两式相减得:![]()
![]() ……8分
……8分
![]() ,即
,即![]() 是以
是以![]() 为公比,以
为公比,以![]() 为首项的等比数列
为首项的等比数列
![]() ……10分
……10分
![]() 也适合
也适合
![]() ……12分
……12分
20.解:(1)由![]() 得点P在圆
得点P在圆![]() 上, ………1分
上, ………1分
解方程组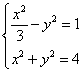 得
得![]() 或
或![]() ………5分
………5分
(2) 由题意得椭圆方程:![]() ……7分
……7分
由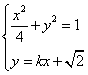 得
得![]()
设![]() ……8分
……8分
则![]()
![]() ……10分
……10分
![]() 又由
又由![]() 得
得![]() ,
,
![]() ……12分
……12分
21.解:(1)散点图为:
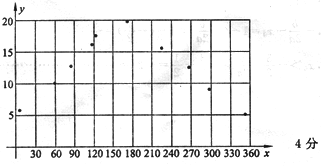
(2)由散点图知细菌存活时间与日期序号之间的函数关系近似为![]() ,由图形知函数的最大值为19.4,最小值为5.4,即,
,由图形知函数的最大值为19.4,最小值为5.4,即,![]() ……5分
……5分
由19.4-5.4=14得A=7;由19.4+5.4=24.8得t=12.4;又T=365,![]() ,
,
当x=172时,![]()
![]() ……8分
……8分
(3)由y>15.9得![]() ,
,
![]() 解得112
解得112![]() x
x![]() 232 ……11分
232 ……11分
答该种细菌大约有121天(或122天)中存活时间大于15.9小时……12分
22.解:(1)证明:f(1)=0 ![]()
![]()
![]() 的图象与x轴有两个相异交点……4分
的图象与x轴有两个相异交点……4分
(2)证明:令![]() .则
.则
![]() =
=
![]()
因此 方程![]() 必有一实根在区间
必有一实根在区间![]() 内……8分
内……8分
(3)证明:
![]() 有解
有解
![]() 由(1)知b=-(a+c),故
由(1)知b=-(a+c),故
![]() ……10分
……10分
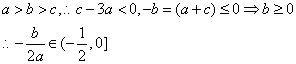 ……12分
……12分
f(1)=0
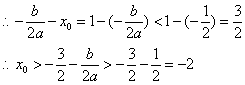 ……14分
……14分