铜陵三中高三综合测试数学试卷(理)2007。4
姓名 得分
一.选择题:本大题共有12小题,每小题5分,共60分.
1.设集合![]() A∪(CIB)=
A∪(CIB)=
A.{1} B.{1,2} C.{2} D.{0,1,2}
2.抛物线y=ax2的准线方程是y=1,则a的值为
A.![]() B.
B.![]() C.4
D.-4
C.4
D.-4
3.命题p:若a、b∈R,则a+b>1是a+b>1的充分而不必要条件;
命题q:函数y=![]() 的定义域是(-∞,-1
的定义域是(-∞,-1![]() ∪[3,+∞
∪[3,+∞![]() .则
.则
A.p假q真 B.“p且q”为真 C.p真q假 D. “p或q”为假
4. 如果将一组数据中的每一个数据都加上同一个非零常数,那么这组数据的平均数和方差的变化情况为
A.平均数和方差都不变 B.平均数不变,方差改变
C.平均数改变,方差不变 D.平均数和方差都改变
5. 已知函数![]() 的反函数为
的反函数为![]() ,则
,则![]() 的解集为
的解集为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知等比数列{an}中,am·am+10=a,am+50·am+60=b,m∈N+,则am+125·am+135等于
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
7.已知直线m、n与平面α、β,给出下列三个命题:
①若![]() ②若
②若![]()
③若![]() 其中真命题的个数是
其中真命题的个数是
A.0 B.1 C.2 D.3
8.定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3,5]时,f(x)=2-x-4,则
A.f(sin![]() )<f(cos
)<f(cos![]() )
B.f(sin1)>f(cos1)
)
B.f(sin1)>f(cos1)
C.f(cos![]() )<f(sin
)<f(sin![]() )
D.f(cos2)>f(sin2)
)
D.f(cos2)>f(sin2)
9.在坐标平面上,不等式组![]() 所表示的平面区域的面积为
所表示的平面区域的面积为
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
10.已知正方体ABCD—A1B1C1D1的棱长为1,P∈BC1,Q∈BC,则D1P+PQ的最小值是
A.2 B.![]() C.
C.![]() D.
D.![]()
11.若点![]() 是
是![]() 的外心,且
的外心,且![]() ,则
,则![]() 的内角
的内角![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.某校高三8个班级的师生为庆祝第二十一个教师节,每个班学生准备了一个节目,已排成节目单.开演前又增加了3个教师节目,其中2个独唱节目,1个朗诵节目.如果将这3个节目插入原节目单中,要求教师的节目不排在第一个和最后一个,并且2个独唱节目不连续演出,那么不同的插法有
A.294种 B.308种 C. 378种 D.392种
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二.填空题:本大题共6小题,每小题4分,共24分.
13.已知![]() 为实数,
为实数,![]() 展开式中
展开式中![]() 的系数为
的系数为![]() ,则
,则![]() .
.
14.函数![]() 的单调递减区间为
.
的单调递减区间为
.
15.把曲线![]() 按向量a=(-1,2)平移后得到曲线C2,曲线C2有一条准线方程为
按向量a=(-1,2)平移后得到曲线C2,曲线C2有一条准线方程为![]() ,则
,则![]() 的值为
的值为
16.已知![]() 是
是![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,则
,则![]() .
.
17.若不等式x-4+3-x<a的解集是空集,则实数a的取值范围是 .
18. 以下四个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,![]() ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作该圆的动弦AB,O为坐标原点,若![]() 则动点
则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
③方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
三、解答题:本大小题共5小题,共66分. 解答应写出文字说明、证明过程或演算步骤.
19. 已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A,B,C的大小。
20、口袋里装有红色和白色共36个不同的球,且红色球多于白色球.从袋子中取出2个球,若是同色的概率为![]() ,求:
,求:
(1) 袋中红色、白色球各是多少?(2) 从袋中任取3个小球,至少有一个红色球的概率为多少?
21.如图,在四棱锥![]() 中,底面
中,底面![]() 是一直角梯形,
是一直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 平面
平面![]() ,
,![]() 与底面成
与底面成![]() 角.
角.
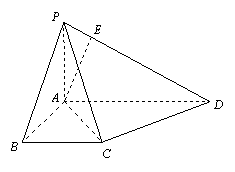 (Ⅰ) 求证:平面
(Ⅰ) 求证:平面![]() 平面
平面![]() ;(Ⅱ) 求二面角
;(Ⅱ) 求二面角![]() 的大小;
的大小;
(Ⅲ) 若![]() ,
,![]() 为垂足,求异面直线
为垂足,求异面直线![]() 与
与
![]() 所成角的大小.
所成角的大小.
22.已知椭圆![]() 为常数,且
为常数,且![]() ,向量
,向量![]() ,过点
,过点![]() 且以
且以![]() 为方向向量的直线与椭圆交于点
为方向向量的直线与椭圆交于点![]() ,直线
,直线![]() 交椭圆于点
交椭圆于点![]() (
(![]() 为坐标原点).
为坐标原点).
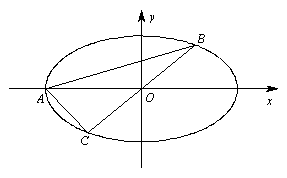 (Ⅰ) 用
(Ⅰ) 用![]() 表示
表示![]() 的面积
的面积![]() ;
;
(Ⅱ) 若![]() ,求
,求![]() 的最大值.
的最大值.
23.设![]() =
=![]() (a>0)为奇函数,且
(a>0)为奇函数,且![]() min=
min=![]() ,数列{an}与{bn}满足如下关系:a1=2,
,数列{an}与{bn}满足如下关系:a1=2, ![]() ,
,![]() .
.
(1)求f(x)的解析表达式;(2) 证明:当n∈N+时, 有bn![]()
![]() .
.
答案:一.选择题:每小题5分,共60分.
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答 案 | D | B | A | C | B | C | C | D | B | C | D | D |
二.填空题:每小题4分,共24分.
(13)![]() (14) (0,1)
(15)5 (16) --1 (17) (-∞,1]( 18 )③、④
(14) (0,1)
(15)5 (16) --1 (17) (-∞,1]( 18 )③、④
19.解: 由sinA(sinB+cosB)-sinC=0,得sinA(sinB+cosB)-sin(A+B)=0
所以 sinAsinB+sinAcosB-sinAcosB-cosAsinB=0
即 sinB(sinA-cosA)=0
因为 B∈(0,π),所以sinB≠0,从而cosA=sinA
由 A∈(0,π),知A=![]() ,从而B+C=
,从而B+C=![]()
由sinB+cos2C=0得sinB+cos2(![]() -B)=0
-B)=0
即 sinB-sin2B=0,亦即sinB-2sinBcosB=0
由此得 ![]()
所以![]()
20.(1)令红色球为x个,则依题意得![]() ,
(3分)
,
(3分)
所以![]() 得x=15或x=21,又红色球多于白色球,所以x=21.所以红色球为21个,白色球为15个.
( 6分)
得x=15或x=21,又红色球多于白色球,所以x=21.所以红色球为21个,白色球为15个.
( 6分)
(2)设从袋中任取3个小球,至少有一个红色球的事件为A,均为白色球的事件为B,
则P(B)=1--P(A)=![]() =
=![]() (12分)
(12分)
21.解:(Ⅰ) 证明:∵![]() ,∴
,∴![]() .……………………………1分
.……………………………1分
∵![]() 底面
底面![]() ,∴
,∴![]() .………………………………………2分
.………………………………………2分
又∵![]() ,∴
,∴![]() 平面
平面![]() .…………………………………3分
.…………………………………3分
∵![]() 平面
平面![]() ,∴平面
,∴平面![]()
![]() 平面
平面![]() .…………………………4分
.…………………………4分
(Ⅱ) 解:作![]() ,垂足为
,垂足为![]() .
.
∵平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,
,
∴![]()
![]() 平面
平面![]() .
.
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,由三垂线定理,得
,由三垂线定理,得![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角.………………………………6分
的平面角.………………………………6分
∵![]() 与底面
与底面![]() 成
成![]() 角,∴
角,∴![]() .
.
∴![]() .
.
∴![]() .
.
在![]() 中,
中,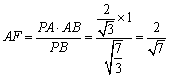 ,……………………7分
,……………………7分
在![]() 中,
中,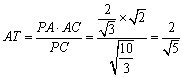 ,………………8分
,………………8分
∴在![]() 中,
中,![]() .
.
因此,二面角![]() 的平面角为
的平面角为![]() .…………………9分
.…………………9分
(Ⅲ) 设![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,连结
的中点,连结![]() 、
、![]() 、
、![]() ,则
,则![]() .
.
∵![]() ,且
,且![]() ,∴四边形
,∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
∴![]() 或它的补角就是异面直线
或它的补角就是异面直线![]() 与
与![]() 所成角.……………11分
所成角.……………11分
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
![]() ,12分
,12分
∴在![]() 中,
中,![]() .…………13分
.…………13分
因此,异面直线![]() 与
与![]() 所成角为
所成角为![]() .……………………14分
.……………………14分
22解:(Ⅰ) 直线![]() 的方程为
的方程为![]() .………………………………………2分
.………………………………………2分
由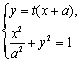 得
得![]() .…………………………3分
.…………………………3分
∴![]() 或
或![]() ,即点
,即点![]() 的纵坐标为
的纵坐标为![]() .…………4分
.…………4分
∵点![]() 与点
与点![]() 关于原点
关于原点![]() 对称,
对称,
∴![]() .…………6分
.…………6分
(Ⅱ) 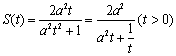 .
.
当![]() 时,
时,![]() ,
,![]() ,
,
当且仅当![]() 时,
时,![]() .……………………………………9分
.……………………………………9分
当![]() 时,可证
时,可证![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
∴![]() 在
在![]() 上单调递增.
上单调递增.
∴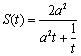 在
在![]() 上单调递减.
上单调递减.
∴当![]() 时,
时,![]() .…………………………………13分
.…………………………………13分
综上可得,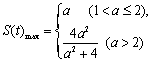 .…………………………14分
.…………………………14分
23.解:由f(x)是奇函数,得 b=c=0, (3分)
由f(x)min=![]() ,得a=2,故f(x)=
,得a=2,故f(x)= ![]() (6分)
(6分)
(2) ![]() =
=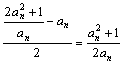 ,
,
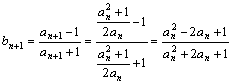 =
=![]() =
=![]() (8分)
(8分)
∴![]() =
=![]() =
=![]() =…=
=…=![]() ,而b1=
,而b1=![]()
∴![]() =
=![]() (10分)
(10分)
当n=1时, b1=![]() ,命题成立,
(12分)
,命题成立,
(12分)
当n≥2时
∵2n-1=(1+1)n-1=1+![]() ≥1+
≥1+![]() =n
=n
∴![]() <
<![]() ,即 bn≤
,即 bn≤![]() .
(14分)
.
(14分)
注:不讨论n=1的情况扣2分.