上海市郊区部分区县2007年高三调研考试数学卷2007年4月
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 1—12 | 13—16 | 17 | 18 | 19 | 20 | 21 | 22 | ||
| 得 分 | |||||||||
考生注意:
1.本试卷共有22道试题,满分150分.考试时间120分钟.请考生用钢笔或圆珠笔将答案直接写在试卷上.
2.本试卷部分记号采用非试验教材的表示法,使用试验教材的考生请注意,试卷中的![]() 相当于试验教材中的
相当于试验教材中的![]() ,
,![]() 相当于试验教材中的
相当于试验教材中的![]() .
.
|
一.填空题 (本大题满分48分)本大题共有12题,只要求直接
填写结果,每题填对得4分,否则一律得零分.
1.已知![]() ,
,![]() (
(![]() 是虚数单位),若
是虚数单位),若![]() 为实数,则实数
为实数,则实数![]() 的值是________.
的值是________.
2.若直线![]() 与直线
与直线![]() 互相垂直,则
互相垂直,则![]() ___________.
___________.
3.已知正三棱锥底面边长为![]() ,侧棱与底面成
,侧棱与底面成![]() 角,则三棱锥的体积为____________.
角,则三棱锥的体积为____________.
4.设![]() ,
,![]() ,则
,则![]() ______________.
______________.
5.(理)已知![]() ,则
,则![]() ____________ .
____________ .
(文)已知![]() (
(![]() ),若
),若![]() ,则
,则![]() __________.
__________.
6.(理)在极坐标系中,曲线![]() 与曲线
与曲线![]() 有__________个公共点.
有__________个公共点.
(文)某工程由下列工序组成,则工程总时数为_____________天.
| 工序 |
|
|
|
|
|
|
| 紧前工序 | — | — |
|
|
|
|
| 工时数(天) |
|
|
|
|
|
|
7.设![]() 为正整数,抛物线
为正整数,抛物线![]() 在
在![]() 轴上截得的线段长为
轴上截得的线段长为![]() ,则
,则
![]() _______________.
_______________.
8.点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 距离最短的点,则
距离最短的点,则![]() 到抛物线焦点的距离
到抛物线焦点的距离
是_____________.
9.已知向量![]() ,
,![]() ,
,![]() ,若
,若![]() 、
、![]() 的夹角为
的夹角为![]() ,则
,则
![]() 的取值范围是_______________________.
的取值范围是_______________________.
10.在某次数学考试中,学号为![]() (
(![]() )的学生的考试成绩为
)的学生的考试成绩为![]() ,且
,且
![]() ,则满足
,则满足![]() 的概率为
的概率为
______________(用分数表示结果).
11.对于实数![]() ,用
,用![]() 表示不超过
表示不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() .
.
(理)若![]() 为正整数,
为正整数,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,则
项和,则![]() _____________.
_____________.
(文)若![]() 为正整数,
为正整数,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,则
项和,则![]() ___________.
___________.
12.(理)设![]() 且
且![]() ,若函数
,若函数![]() 的图像与直线
的图像与直线![]() 恒有公共点,
恒有公共点,
则![]() 、
、![]() 应满足的条件为____________________________________.
应满足的条件为____________________________________.
(文)设![]() ,若函数
,若函数![]() 的图像与直线
的图像与直线![]() 恒有公共点,则
恒有公共点,则![]() 的取值
的取值
范围为_______________________________.
二.选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的圆括号内,选对得4分,不选、选错或者选出的代号超过一个(不论是否都写在圆括号内),一律得零分.
13.△![]() 中,“
中,“![]() ”是“
”是“![]() ”的…………………………………( )
”的…………………………………( )
(A) 充分非必要条件. (B) 必要非充分条件.
(C) 充要条件. (D) 既非充分又非必要条件.
14.若直线![]() (
(![]() )将圆
)将圆![]() 分成两段相等的
分成两段相等的
弧,则![]() 等于………………………………………………………………………( )
等于………………………………………………………………………( )
(A) ![]() .
(B)
.
(B) ![]() .
(C)
.
(C) ![]() .
(D)
.
(D) ![]() .
.
15.制作一个面积为![]()
![]() ,形状为直角三角形的钢框架,有下列四种长度的钢管可供选用,
,形状为直角三角形的钢框架,有下列四种长度的钢管可供选用,
则最合适(既够用,又剩余最少)的长度为……………………………………………( )
(A) ![]()
![]() .
(B)
.
(B) ![]()
![]() .
(C)
.
(C) ![]()
![]() .
(D)
.
(D) ![]()
![]() .
.
16.(理)若函数![]() (
(![]() 且
且![]() )在区间
)在区间![]() 上是增函数,则
上是增函数,则![]()
在区间![]() 上为…………………………………………………………………( )
上为…………………………………………………………………( )
(A) 增函数且有最大值. (B) 增函数且无最大值
(C) 减函数且有最小值. (D) 减函数且无最小值.
(文)已知函数![]() (
(![]() )在区间
)在区间![]() 上是增函数,则函数
上是增函数,则函数![]() 在区间
在区间![]() 上的单调性为………………………………………( )
上的单调性为………………………………………( )
(A) 先减后增. (B) 先增后减. (C) 单调递减. (D) 单调递增.
三.解答题 (本大题满分86分)本大题共有6题,解答下列各题必须写出必要的步骤.
17. (本题满分12分)设![]() ,
,![]() (
(![]() 为实数且
为实数且![]() ,
,![]() 为虚数单位).
为虚数单位).
求函数![]() 的值域.
的值域.
18. (本题满分12分)
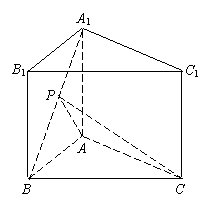 (理)在直三棱柱
(理)在直三棱柱![]() 中,底面△
中,底面△![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
, ![]() 为
为![]() 的中点,且
的中点,且![]() ,求二面角
,求二面角![]() 的大小.
的大小.
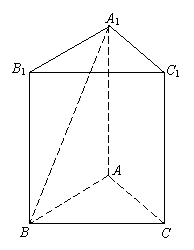 (文)底面边长为
(文)底面边长为![]() 的正三棱柱的体积为
的正三棱柱的体积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
19.(本题满分14分) 本题共有2个小题,理科第1小题满分8分,第2小题满分6分;文科第1小题满分6分,第2小题满分8分.
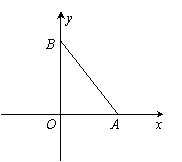
如图,点![]() 、
、![]() 分别是
分别是![]() 轴和
轴和![]() 轴正半轴上的定点,动点
轴正半轴上的定点,动点![]() 满足
满足![]() ,点
,点![]() 满足
满足![]() .
.
(理)(1)用![]() 与
与![]() 来表示
来表示![]() ;
;
(2)当向量![]() 与
与![]() 的夹角
的夹角![]() 为何值时,
为何值时,![]() 的值最大,并求出此最大值.
的值最大,并求出此最大值.
(文)(1)用![]() ,
,![]() ,
,![]() ,
,![]() 来表示
来表示![]() ;
;
(2)求![]() 的最大值,并求出当
的最大值,并求出当![]() 取最大值时点
取最大值时点![]() 的坐标.
的坐标.
 |
20. (本题满分14分)本题共有2个小题,第1小题满分4分,第2小题满分10分.
甲、乙两公司生产同一种新产品,经测算,对于任意![]() ,存在两个函数
,存在两个函数![]() ,
,![]() ,当甲公司投入
,当甲公司投入![]() 万元用于产品的宣传时,若乙公司投入的宣传费小于
万元用于产品的宣传时,若乙公司投入的宣传费小于![]() 万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入
万元,则乙公司有失败的风险,否则无失败风险;当乙公司投入![]() 万元用于产品的宣传时,若甲公司投入的宣传费小于
万元用于产品的宣传时,若甲公司投入的宣传费小于![]() 万元,则甲公司有失败的风险,否则无失败风险.
万元,则甲公司有失败的风险,否则无失败风险.
(1)解释![]() ,
,![]() 的实际意义;
的实际意义;
(2)当![]() ,
,![]()
![]() 时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用.问此时甲、乙两公司各应投入多少宣传费?
时,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用.问此时甲、乙两公司各应投入多少宣传费?
21. (本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.
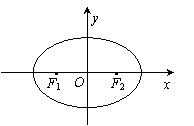
设椭圆![]()
![]() (
(![]() )的两个焦点是
)的两个焦点是![]() 和
和![]() (
(![]() ),且椭圆
),且椭圆![]() 与圆
与圆![]() 有公共点.
有公共点.
(1)求![]() 的取值范围;
的取值范围;
(2)(理)若椭圆上的点到焦点的最短距离为![]() ,求椭圆的方程;
,求椭圆的方程;
(文)如果椭圆的两个焦点与短轴的两个端点恰好是正方形的四个顶点,求椭圆的方程;
(3)(理)对(2)中的椭圆![]() ,直线
,直线![]()
![]() (
(![]() )与
)与![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,若线段
,若线段![]() 的垂直平分线恒过点
的垂直平分线恒过点![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(文)过(2)中椭圆右焦点![]() 且不与坐标轴垂直的直线
且不与坐标轴垂直的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的横坐标的取值范围.
的横坐标的取值范围.
 |
22. (本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
我们用![]() 和
和![]() 分别表示实数
分别表示实数![]() 中的最小者和最大者.
中的最小者和最大者.
(1)设![]() ,
,![]() ,
,![]() ,函数
,函数![]() 的值域为
的值域为![]() ,函数
,函数![]() 的值域为
的值域为![]() ,求
,求![]() ;
;
(2)数学课上老师提出了下面的问题:设![]() ,
,![]() ,…,
,…,![]() 为实数,
为实数,![]() ,求函数
,求函数
![]() (
(![]() )的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数
)的最小值或最大值.为了方便探究,遵循从特殊到一般的原则,老师让学生先解决两个特例:求函数![]() 和
和![]() 的最值.
的最值.
学生甲得出的结论是:![]() ,且
,且![]() 无最大值.
无最大值.
学生乙得出的结论是:![]() ,且
,且![]() 无最小值.
无最小值.
请选择两个学生得出的结论中的一个,说明其成立的理由;
(3)试对老师提出的问题进行研究,写出你所得到的结论并加以证明(如果结论是分类的,请选择一种情况加以证明).
郊区部分区县高三调研考试数学试卷参考答案与评分标准
一、填空题(每小题4分,满分48分)
1.![]() ;2.
;2.![]() ;3.
;3.![]() ;4.
;4.![]() ;5.(理)
;5.(理)![]() ;(文)
;(文)![]() ;6.(理)
;6.(理)![]() ;(文)
;(文)![]() ;7.
;7.![]() ;
;
8.![]() ;9.
;9.![]() ;10.
;10.![]() ;11.(理)
;11.(理)![]() ;(文)
;(文)![]() ;
;
12.(理)![]() 时
时![]() ,
,![]() 时
时![]() .(文)
.(文)![]() .
.
二、选择题(每小题4分,满分16分)
13.C;14.D;15.B;16.(理)D.(文)D.
三、解答题
17.解:![]() ,……(3分)
,……(3分)
∴ ![]() …………(5分)
…………(5分)
![]()
![]() ,…………(8分)
,…………(8分)
∵ ![]() ,∴
,∴ ![]() ,
,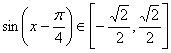 ,
,
∴ 函数![]() 的值域为
的值域为![]() .…………(12分)
.…………(12分)
18.(理)解法一:∵ ![]() 为
为![]() 的中点,且
的中点,且![]() ,∴
,∴ ![]() ,
,
设![]() ,则
,则![]() ,于是
,于是![]() ,所以
,所以 ![]() .……(4分)
.……(4分)
由![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,所以
,所以![]() ,
,
∴ ![]() 是二面角
是二面角![]() 的平面角.…………(8分)
的平面角.…………(8分)
∵ △![]() 是等腰直角三角形,∴
是等腰直角三角形,∴ ![]() ,…………(10分)
,…………(10分)
即二面角![]() 的大小是
的大小是![]() .……………………(12分)
.……………………(12分)
(理)解法二:以![]() 为原点,
为原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建
轴,建
立空间直角坐标系,设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,由
,由![]() ,
,
得![]() ,即
,即![]() ,所以
,所以![]() .…………(4分)
.…………(4分)
平面![]() 的一个法向量为
的一个法向量为![]() ,设面
,设面![]() 的一个法向量是
的一个法向量是![]() ,则由
,则由
![]() ,
,![]() ,得
,得![]() ,
,![]() ,∴
,∴ ![]() ,…………(8分)
,…………(8分)
设![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() .…………(10分)
.…………(10分)
∴二面角![]() 的大小是
的大小是![]() .………………(12分)
.………………(12分)
(文)设![]() ,∵ 正三棱柱的体积为
,∵ 正三棱柱的体积为![]() ,∴
,∴ ![]() ,
,
∴ ![]() .…………(4分)
.…………(4分)
连结![]() ,∵
,∵ ![]() ∥
∥![]() ,∴
,∴ ![]() (或其补角)就是异面直线
(或其补角)就是异面直线![]() 与
与![]() 所成
所成
的角.…………(6分)
在△![]() 中,
中,![]() ,
,![]() ,∴
,∴ ![]() .………(10分)
.………(10分)
∴ ![]() .
.
∴ 异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .…………………………(12分)
.…………………………(12分)
(或![]() ,或
,或![]() )
)
19.(理)解法一:(1)由已知可得![]() ,又
,又![]() ,
,
∴ ![]() ……(2分)
……(2分)
所以,![]()
![]() .…………(8分)
.…………(8分)
(或![]() )
)
(2)由(1),![]()
![]() ,…………(12分)
,…………(12分)
∴ 当![]() ,即向量
,即向量![]() 与
与![]() 的夹角
的夹角![]() 时,
时,![]() 取最大值
取最大值![]() .…(14分)
.…(14分)
解法二:(1)由已知可得![]() ,∴
,∴ ![]() ,
,![]() ,
,
∴ ![]() ,……(2分)
,……(2分)
由已知,![]() ,
,![]() ,
,![]() ,
,![]()
∴ ![]() .…………(8分)
.…………(8分)
(2)由(1)![]()
![]() …………(10分)
…………(10分)
当且仅当![]() 时,等号成立,此时
时,等号成立,此时![]() ,而
,而![]() ,…(12分)
,…(12分)
所以![]() 与
与![]() 的夹角
的夹角![]() 时,
时,![]() 取得最大值
取得最大值![]() .……(14分)
.……(14分)
19.(文)(1)由已知可得![]() ,
,
∴ ![]() ,
,![]() ,(2分)
,(2分)
∴ ![]() ,……(6分)
,……(6分)
(或![]() )
)
(2)由(1)![]()
![]() …………(10分)
…………(10分)
当且仅当![]() 时,等号成立,此时
时,等号成立,此时![]() ,
,
∴ 当点![]() 的坐标为
的坐标为![]() 时,
时,![]() 取最大值
取最大值![]() .………………(14分)
.………………(14分)
20.解:(1)![]() 的实际意义是当甲公司不进行产品宣传时,乙公司为了保证无失败
的实际意义是当甲公司不进行产品宣传时,乙公司为了保证无失败
风险,至少要投入![]() 万元用于产品宣传;
万元用于产品宣传;![]() 的实际意义是当乙公司不进行产
的实际意义是当乙公司不进行产
品宣传时,甲公司为了保证无失败风险,至少要投入![]() 万元用于产品宣传.…(4分)
万元用于产品宣传.…(4分)
(2)设甲公司投入宣传费用![]() 万元,乙公司投入宣传费用
万元,乙公司投入宣传费用![]() 万元,则当且仅当
万元,则当且仅当
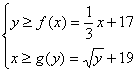 时,双方均无失败的风险.…………(8分)
时,双方均无失败的风险.…………(8分)
∴ ![]() ,解得
,解得![]() ,…………(12分)
,…………(12分)
从而![]() ,……(13分)
,……(13分)
即甲、乙两公司应分别投入![]() 万元和
万元和![]() 万元进行产品宣传.…………(14分)
万元进行产品宣传.…………(14分)
21.解:(1)由已知,![]() ,
,
∴ 方程组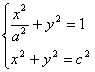 有实数解,从而
有实数解,从而![]() ,……(3分)
,……(3分)
故![]() ,所以
,所以![]() ,即
,即![]() 的取值范围是
的取值范围是![]() .…………(4分)
.…………(4分)
(2)(理)设椭圆上的点![]() 到一个焦点
到一个焦点![]() 的距离为
的距离为![]() ,
,
则![]()
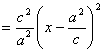 (
(![]() ).……………………(6分)
).……………………(6分)
∵ ![]() ,∴ 当
,∴ 当![]() 时,
时,![]() ,……(7分)
,……(7分)
于是,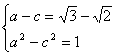 ,解得
,解得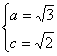 .…………(9分)
.…………(9分)
∴ 所求椭圆方程为![]() .…………(10分)
.…………(10分)
(直接给出![]() 的扣3分)
的扣3分)
(2)(文)由已知可得 ![]() ,从而
,从而![]() ,……(8分)
,……(8分)
所以所求椭圆方程是![]() .…………(10分)
.…………(10分)
(3)(理)由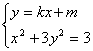 得
得![]() (*)
(*)
∵ 直线![]() 与椭圆交于不同两点, ∴ △
与椭圆交于不同两点, ∴ △![]() ,即
,即![]() .①……(12分)
.①……(12分)
设![]() 、
、![]() ,则
,则![]() 、
、![]() 是方程(*)的两个实数解,
是方程(*)的两个实数解,
∴ ![]() ,∴ 线段
,∴ 线段![]() 的中点为
的中点为![]() ,
,
又∵ 线段![]() 的垂直平分线恒过点
的垂直平分线恒过点![]() ,∴
,∴ ![]() ,
,
即![]() ,即
,即![]() ②………………(14分)
②………………(14分)
由①,②得![]() ,
,![]() ,又由②得
,又由②得![]() ,
,
∴ 实数![]() 的取值范围是
的取值范围是![]() .…………(16分)
.…………(16分)
(3)(文)![]() ,由题意,直线
,由题意,直线![]() 的斜率存在且不为
的斜率存在且不为![]() ,设直线
,设直线![]() 的方程为:
的方程为:
![]() ,由
,由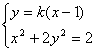 得,
得,![]() ……(*)
……(*)
设![]() ,
,![]() ,则
,则![]() 是方程(*)的两个实数解,于是
是方程(*)的两个实数解,于是![]() ,
,
则线段![]() 的中点为
的中点为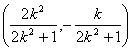 .……(12分)
.……(12分)
∴ 线段![]() 的垂直平分线的方程为
的垂直平分线的方程为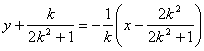 ,
,
在上式中令![]() ,得点
,得点![]() 的横坐标为
的横坐标为![]() .…………(14分)
.…………(14分)
∴ 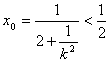 ,所以点
,所以点![]() 的横坐标的取值范围是
的横坐标的取值范围是![]() .…………(16分)
.…………(16分)
22.解(1)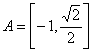 ,
,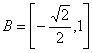 ,∴
,∴ 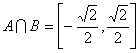 .……(4分)
.……(4分)
(2)若选择学生甲的结论,则说明如下,
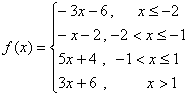 ,于是
,于是![]() 在区间
在区间![]() 上是减函数,在
上是减函数,在![]() 上
上
是减函数,在![]() 上是增函数,在
上是增函数,在![]() 上是增函数.……(8分)
上是增函数.……(8分)
所以函数![]() 的最小值是
的最小值是![]() ,且函数
,且函数![]() 没有最大值.(10分)
没有最大值.(10分)
若选择学生乙的结论,则说明如下,
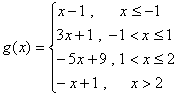 ,于是
,于是![]() 在区间
在区间![]() 上是增函数,在
上是增函数,在![]() 上是
上是
增函数,在![]() 上是减函数,在
上是减函数,在![]() 上是减函数.…………(8分)
上是减函数.…………(8分)
所以函数![]() 的最大值是
的最大值是![]() ,且函数
,且函数![]() 没有最小值.(10 分)(3)结论:
没有最小值.(10 分)(3)结论:
若![]() ,则
,则![]() ;
;
若![]() ,则
,则![]()
![]() ;
;
若![]() ,则
,则![]() ,
,
![]()
![]()
(写出每个结论得1分,共3分,证明为5分)
以第一个结论为例证明如下:
∵ ![]() ,∴ 当
,∴ 当![]() 时,
时,
![]() ,是减函数,
,是减函数,
当![]() 时,
时,
![]() ,是增函数
,是增函数
当![]() 时,函数
时,函数![]() 的图像是以点
的图像是以点![]() ,
,![]() ,…,
,…,![]()
为端点的一系列互相连接的折线所组成,
所以有![]() .
.