高三年级数学十二月月考试题
数 学 试 题（理）
命题：王宪生 审稿：张智 校对：胡华川
本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分，用时120分钟.
参考公式：
如果事件A、B互斥，那么 球的表面积公式
P(A+B)=P(A)+P(B) S=4
R2
如果事件A、B相互独立，那么 其中R表示球的半径
P(AB)=P(A)P(B) 球的体积公式
如果事件A在一次试验中发生的概率是 V=
R3
P，那么
次独立重复试验中恰好发生
其中R表示球的半径
次的概率
第Ⅰ卷（选择题，共50分）
一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1．已知向量
，
和
，若
，则向量
与
的夹角
=（ ）
A．
B．
C．
D．
2．设全集U=R，已知非空集合P=
与集合M=
之间满足P
=P，则实数
的取值范围是（ ）
A．
B．
C．
D．
3．已知角
的终边经过点P（
，
），且
，则的一个值是（ ）
A．
B．
C．
D．
4．“一个几何体在三个两两垂直的平面上的射影是三个全等的圆”是“这个几何体是球”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
5．已知
是互不相等的三个实数，且
成等差数列，则
（ ）
A．
B．
C．
D．
6．已知P1（
）是直线
上的一点，P2（
）是直线
外的一点，则由方程
表示的直线与直线的位置关系是（ ）
A．互相重合 B．互相平行 C．互相垂直 D．互相斜交
7．一个正四棱锥的高为2
，侧棱与底面所成的角为45°，则这一正四棱锥的斜高等于（ ）
A．
B．
C．
D．
8．从一块短轴长为
的椭圆形玻璃镜中划出一块面积最大的矩形，其面积的取值范围是
，则这一椭圆离心率
的取值范围是（ ）
A．
B．
C．
D．
9．设函数
的导数
的最大值为3，则
的图象的一条对称轴的方程是（ ）
A．
B．
C．
D．
10．设表示复数
R）的点Z
位于不等式组
确定的平面区域，对于任意实数，则表示复数
的点W一定位于（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
第Ⅱ卷（非选择题，共100分）
二、填空题：本大题共5小题，每小题5分，共25分. 把答案填在答题卡的相应位置上.
11．以曲线
上的任意一点为圆心作圆与直线
相切，这些圆必过一定点，则这一定点的坐标是_______________________．
12．曲线C与曲线
的图象关于直线
对称，则曲线C与有一个交点位于区间________________（写出一个长度为1的开区间即可）。
13．已知一个半径为
的球中有一个各条棱长都相等的内接正三棱柱，则这一正三棱柱的体积是_________________．
14．设集合M={
}，
：M
M是从M到M的一个映射，若该映射满足条件[(
)]= ()，则这样的映射共有________________个.
15．已知
是两条相交直线，
是两个不同平面，给出命题：“若
，
，且_____________________，则
”．请利用数学符号语言，在横线上补足条件，使该命题成为一个真命题．
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | ||||||||||
| 题号 | 11 | 12 | 13 | 14 | 15 | |||||
| 答案 | ||||||||||
三、解答题：本大题共6小题，共75分. 解答应写出文字说明、证明过程或演算步骤.
16．（本小题满分12分）已知关于的不等式
的解集为空集，求实数 的取值或取值范围．
17．（本小题满分12分）已知函数
，求该函数的定义域、最小正周期和最大、最小值．
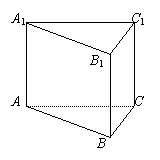
18．（本小题满分12分）已知正三棱柱ABC—A1B1C1的底面边长为1，高为
，点M在侧棱BB1上移动，到底面ABC的距离为，且AM与侧面BCC1所成的角为
；
（I）若在区间
上变化，求的变化范围；
（II）若为
，求
与
所成的角．
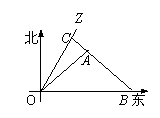
19．（本小题满分12分）如图，一科学考察船从港口
出发，沿北偏东角的射线
方向航行，而在离港口
为正常数）海里的北偏东
角的
处有一个供给科考船物资的小岛，其中已知
．现指挥部需要紧急征调沿海岸线港口正东
海里的
处的补给船，速往小岛装运物资供给科考船．该船沿
方向全速追赶科考船，并在
处相遇．经测算当两船运行的航线与海岸线
围成的三角形
的面积
最小时，这种补给最适宜．
（I）求关于的函数关系式
；
（II）应征调为何值处的船只，补给最适宜？
20．（本小题满分13分）已知
定义在区间
上，且
，又
是其图象上任意两点
．
（Ⅰ）设直线PQ的斜率为k，求证k＜2；
（Ⅱ）若0
，求证
＜1．
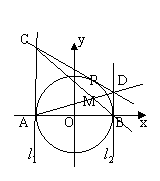
21．（本小题满分14分）如图，圆O：
与轴交于A、B两点，
是分别过A、B点的圆O的切线，过此圆上的另一个点P（P点是圆上任一不与A、B重合的点）作此圆的切线，分别交于C、D点，且AD、BC两直线的交点为M．
（I）当P点运动时，求动点M的轨迹方程；
（II）判断是否存在点Q（，0）（
），使得Q点到（Ⅰ）中轨迹上的点的最近距离为
？若存在，求出所有这样的点Q；若不存在，请说明理由．