高三年级数学十月月考试题
数 学 试 题(理)
命题人:吴校红
第Ⅰ卷(选择题,共50分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设全集为R,![]() ,a为常数,且
,a为常数,且![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.已知函数![]() (a>0且a≠1)满足:对任意实数x1、x2,当
(a>0且a≠1)满足:对任意实数x1、x2,当![]() 时,总有
时,总有![]() ,那么实数a的取值范围是( )
,那么实数a的取值范围是( )
A.(0,3) B.(1,3) C.![]() D.
D.![]()
3.若tan100°=a,则用a表示cos10°的结果为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.设数列{an}是公比为a (a≠1),首项为b的等比数列,Sn是其前n项和,对任意的n∈N+,点(Sn, Sn+1)在( )
A.直线y=ax+b上 B.直线y=ax-b上 C.直线y=bx+a上 D.直线y=bx-a上
5.已知![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的图象( )
的图象( )
A.关于直线x+y=0对称 B.关于直线x- y=0对称
C.关于y轴对称 D.关于原点对称
6.若“p且q”与“┐p或q”均为假命题,则( )
A.p真q假 B.p假q真 C.p与q均真 D.p与q均假
7.若![]() ,则θ角的终边在( )
,则θ角的终边在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.设O为△ABC内部一点,且![]() ,则△AOC的面积与△BOC的面积之比为( )
,则△AOC的面积与△BOC的面积之比为( )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
9.已知函数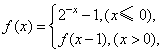 若方程
若方程![]() 有且只有两个不相等的实数根,则实数a的取值范围为( )
有且只有两个不相等的实数根,则实数a的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设定义域、值域均为R的函数![]() 的反函数为
的反函数为![]() 若
若![]() 对一切
对一切![]() 成立,则
成立,则![]() 的值为( )
的值为( )
A.0 B.1 C.-1 D.2
第Ⅱ卷(非选择题,共100分)
二、填空题:本大题共5小题,每小题5分,共25分. 把答案填在答题卡的相应位置上.
11.已知![]() ,坐标原点O在直线AB上的射影为点C,则
,坐标原点O在直线AB上的射影为点C,则![]() ________.
________.
12.定义在R上的奇函数f(x)以4为周期,则![]() 的值为____.
的值为____.
|
(2)每一行除首尾两数外,中间任一数等于它肩上两数之和.
则第n行(n≥2)第2个数an=_____________.
14.已知集合![]() ,
,
![]() 的子集的个数为4,则实数a的取值范围是____________.
的子集的个数为4,则实数a的取值范围是____________.
15.关于函数![]() ,有下列命题:
,有下列命题:
①由![]() 可得
可得![]() 必是
必是![]() 的整数倍;②若
的整数倍;②若![]() ,则
,则![]() ;③函数的图象关于点
;③函数的图象关于点![]() 对称;④函数
对称;④函数![]() 的单调递增区间可由不等式
的单调递增区间可由不等式![]() 求得.
求得.
其中正确命题的序号是____________(注:把你认为正确的命题的序号都填上).
第Ⅰ卷答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | ||||||||||
| 题号 | 11 | 12 | 13 | 14 | 15 | |||||
| 答案 | ||||||||||
三、解答题:本大题共6小题,共75分. 解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)已知函数![]() 的反函数为
的反函数为
![]()
(1)若![]() ,求x的取值集合D;
,求x的取值集合D;
(2)设函数![]() ,当x∈D时,求H(x)的最大值及相应的x值.
,当x∈D时,求H(x)的最大值及相应的x值.
17.(本小题满分13分)已知函数![]() .
.
(1)求函数f(x)的最小正周期T;
(2)在给出的直角坐标系中,画出函数f(x)在![]() 上的图象;
上的图象;
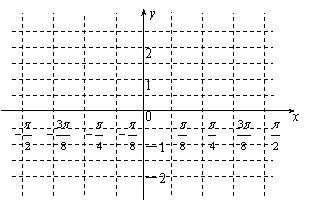 (3)若当
(3)若当![]() 时,f(x)的反函数为
时,f(x)的反函数为![]() ,求
,求![]() 的值.
的值.
18.(本小题满分12分)禽流感疫情的爆发,给疫区禽类养殖户带来了一定的经济损失,某养殖户原来投资20万元,预计第一个月损失的金额是投资额的![]() ,以后每个月损失的金额是上个月损失金额的
,以后每个月损失的金额是上个月损失金额的![]() .
.
(1)三个月中,该养殖户总损失的金额是多少元?
(2)为了扶持禽类养殖,政府决定给予一定的补偿,若该养殖户每月可从政府处领到a万元的补偿金,总共三个月,且每个月损失金额(补贴前)是上个月损失金额(补贴后)的![]() ,若补贴后,该养殖户第三个月仅损失1200元,求a的值以及该养殖户在三个月中,实际总损失为多少元?
,若补贴后,该养殖户第三个月仅损失1200元,求a的值以及该养殖户在三个月中,实际总损失为多少元?
19.(本小题满分14分)若Sn和Tn分别表示数列{an}和{bn}的前n项和,对任意正整数n,![]()
(1)求数列{bn}的通项公式;
(2)在平面直角坐标系内,直线ln的斜率为bn,且与抛物线![]() 有且仅有一个交点,与y轴交于点Dn,记
有且仅有一个交点,与y轴交于点Dn,记![]() ,求dn;
,求dn;
(3)若![]() ,求
,求![]() 的值.
的值.
20.(本小题满分14分)在直角坐标平面中,已知点P1(1,2),P2(2,22),P3(3,23),……,Pn(n,2n),其中n是正整数,对平面上任一点A0,记A1为A0关于点P1的对称点,A2为A1关于点P2的对称点,……,An为An-1关于点Pn的对称点.
(1)求向量![]() 的坐标;
的坐标;
(2)当点A0在曲线C上移动时,点A2的轨迹是函数![]() 的图像,其中f(x)是以3为周期的周期函数,且当
的图像,其中f(x)是以3为周期的周期函数,且当![]() 时,
时,![]() ,求以曲线C为图像的函数g(x)在
,求以曲线C为图像的函数g(x)在![]() 上的解析式;
上的解析式;
(3)对任意偶数n,用n表示向量![]() 的坐标.
的坐标.
21.(本小题满分10分)已知对于正整数a,存在一个以a为二次项系数的整系数二次三项式,具有两个不相等且小于1的正根,求证:a≥5.
参考答案(理)
一、选择题
1.D 2.C 3.B 4.A 5.B 6.A 7.C 8.C 9.C 10.B
二、填空题
11.![]() 12.0 13.
12.0 13.![]() 14.
14.![]() 15.②③
15.②③
三、解答题
16.(1)由![]() 得
得![]()
∵![]() ∴
∴![]()
则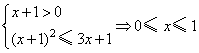 ,∴
,∴![]()
(2)∵![]()
![]()
x∈D,即0≤x≤1,∴![]() ,故
,故![]()
∴H(x)的最大值为![]() ,此时x=1.
,此时x=1.
17.(1)∵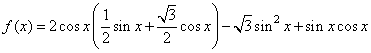
![]()
![]()
∴![]()
(2)图形如图
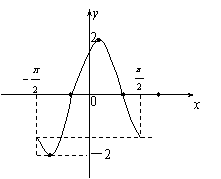
(3)∵![]() 时,
时,![]()
由![]()
∴![]()
∴![]()
18.(1)三个月中,该养殖户总损失的金额为: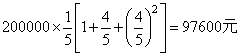
(2)∵该养殖户第一个月实际损失为![]() (万元),
(万元),
第二个月实际损失为:![]() (万元)
(万元)
第三个月实际损失为:![]() (万元)
(万元)
∴![]()
该养殖户在三个月中实际总损失为:![]()
19.(1)∵![]()
当n≥2时,![]()
n=1时也适合 ∴![]()
(2)设ln方程为:![]()
由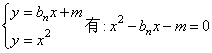
∵直线ln与抛物线有且只有一个交点,
∴![]()
∴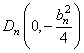
故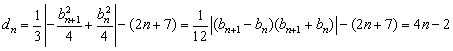
(3)∵![]()
∴![]()
故![]()
20.(1)设![]() ,∵An与An-1关于点
,∵An与An-1关于点![]() 对称,
对称,
∴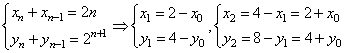
故![]()
(2)∵![]() ,
,
![]() ,而T=3,∴
,而T=3,∴![]()
故当![]() 时,∵
时,∵![]() ,∴
,∴![]() ,由
,由
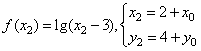 有:
有:
![]()
∴曲线C在![]() 上的解析式为:
上的解析式为:![]()
![]()
(3)∵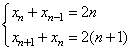
∴![]()
同理可得:![]()
∴![]()
故![]()
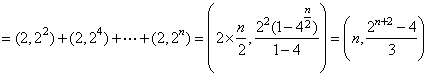 21.设二次三项式为
21.设二次三项式为![]()
依题意有0<x1<1,0<x2<1且x1≠x2
则![]()
又∵![]() 为整系数二次三项式,
为整系数二次三项式,
∴f(0), f(1)均为整数,进而有f(0)≥1,f(1)≥1,故f(0)f(1)≥1.
又∵![]()
由x1≠x2知两不等式等号不能同时成立,
∴![]()
∴![]()
故![]() ∴
∴![]() 又
又![]() ,∴a≥5.
,∴a≥5.