高三年级数学模拟练习3
张春明
1.设m、n是两条不同的直线,α、β是两个不同的平面,考查下列命题,其中正确的命题是 ( )
A.![]() B.
B.![]() ∥
∥![]() ∥
∥![]()
C.![]() ∥
∥![]() D.
D.![]()
2、设![]() 的展开式中x的一项的系数,则
的展开式中x的一项的系数,则![]() 的值是( )
的值是( )
A.16 B.
3.在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目. 若选到男教师的概率为![]() ,则参加联欢会的教师共有( )
,则参加联欢会的教师共有( )
A.120人. B.144人 C.240人 D.360人
4、已知点![]() ,动点M在圆
,动点M在圆![]() 上,动点N在圆
上,动点N在圆![]() 上,则
上,则![]() 的最小值是
( )
的最小值是
( )
A.![]() B.
B.![]() C.1 D.2
C.1 D.2
5.若![]() 为奇函数,
为奇函数,![]() 与
与![]() 关于直线
关于直线![]() 对称,则
对称,则![]() ( )
( )
A.0 B.
6.已知平面α∥平面β,直线l![]() α,点P∈l,平面α、β间的距离为8,则在β内到点P的距离为10且到直线l的距离为9的点的轨迹是
( )
α,点P∈l,平面α、β间的距离为8,则在β内到点P的距离为10且到直线l的距离为9的点的轨迹是
( )
A.一个圆 B.两条直线 C.四个点 D.两个点
 7.定点N(1,0),动点A、B分别在图中抛物线
7.定点N(1,0),动点A、B分别在图中抛物线![]() 及椭圆
及椭圆![]()
的实线部分上运动,且AB∥x轴,则△NAB的周长l取值范围是( )
(A)(![]() ) (B)(
) (B)(![]() ) (C)(
) (C)(![]() ) (D)(
) (D)(![]() )
)
8、设定义域为![]() 的函数
的函数![]() 满足以下条件:①对任意
满足以下条件:①对任意![]() ;②对任意
;②对任意![]() 当
当![]() 时,有
时,有![]() ,则以下不等式不一定成立的是( )
,则以下不等式不一定成立的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题
9.设![]() .映射
.映射![]() 使得B中的元素都有原象.则这样的
使得B中的元素都有原象.则这样的
映射![]() 有
个.
有
个.
10.点![]() 是四边形
是四边形![]() 内一点,满足
内一点,满足![]() ,若
,若![]() ,
,
则![]() .
.
11.已知函数![]() 的图象经过原点O,且在
的图象经过原点O,且在![]() 处取得极值,曲线
处取得极值,曲线![]() 在原点处的切线
在原点处的切线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,且直线
,且直线![]() 的倾斜角为钝角,则
的倾斜角为钝角,则![]() 的单调增区间是
的单调增区间是
12.若不等式![]() 对于任意正整数n恒成立,则实数a的取值范围是
对于任意正整数n恒成立,则实数a的取值范围是
三、解答题
13、已知△ABC的面积S满足![]() ≤S≤3,且
≤S≤3,且![]() ,设
,设![]() 与
与![]() 的夹角为
的夹角为![]()
(1)求![]() 的取值范围;
的取值范围;
(2)求函数![]() 的最小值。
的最小值。
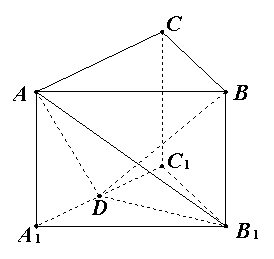 14.如图,在直三棱柱
14.如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
(1)
设平面![]() 与棱
与棱![]() 交于点
交于点![]() ,确定点
,确定点![]() 的位置并给出理由;
的位置并给出理由;
(2)
求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(3)
求二面角![]() 的大小.
的大小.
15. 在![]() 中,已知
中,已知![]() ,
,![]() ,(
,(![]() 为不等于零的常数)
为不等于零的常数)![]() 、
、![]() 两边所在的直线分别与
两边所在的直线分别与![]() 轴交于原点同侧的点
轴交于原点同侧的点![]() 、
、![]() 。设
。设![]() 。
。
(1)求![]() 、
、![]() 两点坐标(用
两点坐标(用![]() 及
及![]() 表示)。
表示)。
(2)若![]() 、
、![]() 满足
满足![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(3)如果存在直线![]()
![]() ,使
,使![]() 与点
与点![]() 的轨迹相交于不同的
的轨迹相交于不同的![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
16.已知![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() ,n=1,2,3…
,n=1,2,3…
(Ⅰ)求证: 数列![]() 为等比数列;
为等比数列;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
江苏省通州高级中学2006-2007 高三数学模拟练习3答案
张春明
BBAD DCBC
二、填空题
9.
36 . 10. 3.
11.![]() ,
,![]()
![]() 12.
12. ![]()
三、解答题
13、已知△ABC的面积S满足![]() ≤S≤3,且
≤S≤3,且![]() ,设
,设![]() 与
与![]() 的夹角为
的夹角为![]()
(1)求![]() 的取值范围;
的取值范围;
(2)求函数![]() 的最小值。
的最小值。
13、(1)∵![]() ∴
∴![]() ∴
∴![]() --------------------2分
--------------------2分
又∵![]() -----------------------------------4分
-----------------------------------4分
∴![]() ≤
≤![]() ≤3 ∴
≤3 ∴![]() ≤
≤![]() ≤1------------------------------------------------5分
≤1------------------------------------------------5分
又∵![]() ∴
∴![]() ≤
≤![]() ≤
≤![]() -----------------------------------------------------6分
-----------------------------------------------------6分
(2)![]() ------------------8分
------------------8分
∵![]() ∴
∴![]() ∴
∴![]() ---------------------10分
---------------------10分
∴当![]() 时
时 ![]() ------------------------------------------------------------12分
------------------------------------------------------------12分
 14.如图,在直三棱柱
14.如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 的中点.
的中点.
(4)
设平面![]() 与棱
与棱![]() 交于点
交于点![]() ,确定点
,确定点![]() 的位置并给出理由;
的位置并给出理由;
(5)
求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(6)
求二面角![]() 的大小.
的大小.
14.(本小题满分14分)
解(1)E是AC的中点.
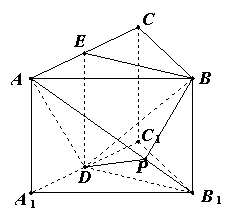 由棱柱的性质知
由棱柱的性质知![]() ∥平面
∥平面![]() ,∵
,∵![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,∴所以
,∴所以![]() ∥
∥![]() ,∴
,∴![]() ∥
∥![]() ,由
,由![]() 是
是![]() 的中点知
的中点知![]() 是
是![]() 中点.
中点.
(2)∵![]() 底面
底面![]() ,∴平面
,∴平面![]() ⊥底面
⊥底面![]() ,过
,过![]() 点作
点作![]() ⊥
⊥![]() ,
,![]() 是垂足,
是垂足,![]() 在
在![]() 的延长线上,∴
的延长线上,∴![]() ⊥平面
⊥平面![]() ,
,![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成角. 在直角
所成角. 在直角![]() 中,
中,![]() ,又
,又![]() ,所以
,所以![]() ,∴
,∴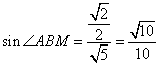 ,
,![]() .
.
(或在△ABC中,∠ABM=∠ABE=∠ABC-∠CBE=![]() )
)
(3)解法一.如图1,在直角![]() 中
中![]() ,在直角
,在直角![]() 中
中![]() ,在直角
,在直角![]() 中
中![]() ,∴
,∴![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() ,
,![]()
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() 是二面角
是二面角![]() 的平面角. ……11分
的平面角. ……11分
连![]() .在等腰
.在等腰![]() 中
中![]() ,在直角
,在直角![]() 中
中![]() ,
,
在![]() 中,
中,![]()
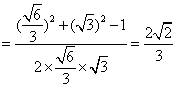 ,
,
∴二面角![]() 的大小为
的大小为![]() .
.
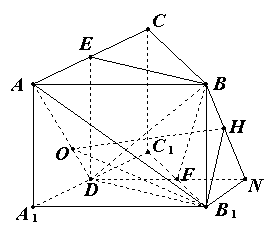 解法二:设平面
解法二:设平面![]() 与棱
与棱![]() 交于点F,则F为
交于点F,则F为![]() 中点,如图,过点
中点,如图,过点![]() 作
作![]() ⊥
⊥![]() ,垂足
,垂足![]() 在
在![]() 的延长线上,连
的延长线上,连![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,作
,作![]() ,
,![]() 为垂足,
为垂足,
∵![]() ,∴
,∴![]() 平面
平面![]() ,作
,作![]() 为垂足,连
为垂足,连![]() ,由三垂线逆定理知
,由三垂线逆定理知![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角.
………………11分
的平面角.
………………11分
在直角![]() 中,得
中,得![]() ,在直角
,在直角![]() 中得
中得![]() ,
,
在![]() 中,
中,![]() ,得
,得![]() ,
,
在直角![]() 中,
中,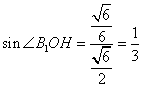 ,所以二面角
,所以二面角![]() 的大小是
的大小是![]() .
.
15. 在![]() 中,已知
中,已知![]() ,
,![]() ,(
,(![]() 为不等于零的常数)
为不等于零的常数)![]() 、
、![]() 两边所在的直线分别与
两边所在的直线分别与![]() 轴交于原点同侧的点
轴交于原点同侧的点![]() 、
、![]() 。设
。设![]() 。
。
(1)求![]() 、
、![]() 两点坐标(用
两点坐标(用![]() 及
及![]() 表示)。
表示)。
(2)若![]() 、
、![]() 满足
满足![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(3)如果存在直线![]()
![]() ,使
,使![]() 与点
与点![]() 的轨迹相交于不同的
的轨迹相交于不同的![]() 、
、![]() 两点,且
两点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
15、解(1)当![]() 时,
时,![]() 轴,当
轴,当![]() 时,
时,![]() 轴,
轴,
与题意不符,所以![]() 1分
1分
由![]() 三点共线得
三点共线得![]() 解得
解得![]() 1分
1分
同理解得![]() 1分
1分
![]() ,
, ![]()
![]() 。 1分
。 1分
(2)因为![]() 所以
所以![]() 2分
2分
化简得![]()
![]() 1分
1分
![]() 轨迹为
轨迹为![]()
![]() 1分
1分
(3)设![]() 中点为
中点为![]() ,
,
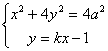
![]()
由![]() 化简得
化简得![]() ① 2分
① 2分
![]()
![]() 2分
2分
![]() 即
即![]()
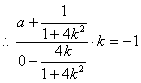 ,
,![]() 即
即![]() ② 2分
② 2分
![]()
![]() 将②代入①得
将②代入①得![]() 得
得![]() 1分
1分
当![]() 时,直线
时,直线![]() 过
过![]() 点,而曲线
点,而曲线![]() 不过
不过![]() ,所以直线与曲线
,所以直线与曲线![]() 只有一个公共点,故
只有一个公共点,故![]() ,
,![]() 且
且![]() 1分
1分
16.已知![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() ,n=1,2,3…
,n=1,2,3…
(Ⅰ)求证: 数列![]() 为等比数列;
为等比数列;
(Ⅱ)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅲ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
20.(本小题14分)
(Ⅰ)解:![]()
![]() ,
,
![]() .
.
![]() .
.
![]() 是以2为公比的等比数列
3分
是以2为公比的等比数列
3分
(Ⅱ)![]() ,
,![]()
![]() .
.
![]() .
4分
.
4分
当![]() 为偶数时,
为偶数时,
![]()
![]()
![]()
![]() ; 6分
; 6分
当![]() 为奇数时,
为奇数时,
![]() n=
n=![]() .
8分
.
8分
综上,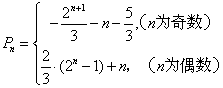 .
9分
.
9分
(Ⅲ)![]() .
.
当=1时,![]()
![]()
当≥2时,
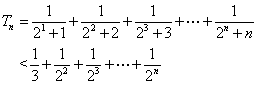
=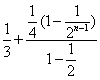
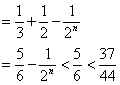
综上可知:任意![]() ,
,![]() .
14分
.
14分
说明:其它正确解法按相应步骤给分.