高三年级数学模拟练习二
一、选择题:
1.已知直线![]() ,直线
,直线![]() 与
与![]() 关于直线
关于直线![]() 对称,则直线
对称,则直线![]() 的斜率为( )
的斜率为( )
A.
![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 设![]() 、
、![]() 是异面直线,则
是异面直线,则
(1)一定存在平面![]() ,使
,使![]() 且
且![]() ∥
∥![]()
(2)一定存在平面![]() ,使
,使![]() 且
且![]()
(3)一定存在平面![]() ,使
,使![]() ,
,![]() 到
到![]() 的距离相等
的距离相等
(4)一定存在平面![]() 、
、![]() ,使
,使![]() ,
,![]() ,且
,且![]()
上述4个命题中正确的个数为 ( )
A.1
B.
3.已知等差数列![]() 的前n项和为Sn,若
的前n项和为Sn,若![]() 成等比数列,则
成等比数列,则![]() 等于( )
等于( )
A.100或-100 B.-
4.已知二次函数f(x)=ax2+bx+c,当x=1时有最大值1,若x∈[m,n](0<m<n)时,函数f(x)的值域为[![]() ,
,![]() ],则
],则![]() 的值为( )
的值为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.已知函数![]() 的图象的一条对称轴方程为直线x=1,若将函数
的图象的一条对称轴方程为直线x=1,若将函数![]() 的图象向右平移b个单位后得到y=sinx的图象,则满足条件的b的值一定为 ( )
的图象向右平移b个单位后得到y=sinx的图象,则满足条件的b的值一定为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.某校高三年级举行的一次演讲比赛共有10位同学参赛,其中一班有3位,二班有2位,其他班有5位. 若采取抽签的方式确定他们的演讲顺序,则一班的3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为( )
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D)
(D)
![]()
7.向量![]() 是不共线的非零向量,
是不共线的非零向量,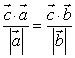 ,则( )
,则( )
A. ![]() B.
B.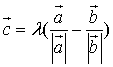
C.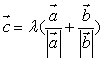 D.
D. 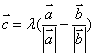
![]() 或
或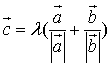
![]()
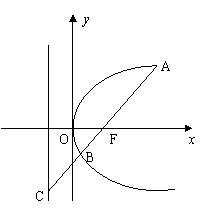
8.如图,过抛物线![]() 的焦点F的直线
的焦点F的直线![]() 交抛物线于点A、B,交其准线于点C,若
交抛物线于点A、B,交其准线于点C,若![]() ,且
,且![]() ,则此抛物线的方程为 (
)
,则此抛物线的方程为 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:
9.在![]() 的展开式中,常数项是
。
的展开式中,常数项是
。
10.不等式log2(x+3-x-1)≥1的解集为 .
11.已知函数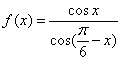 ,则
,则![]() 的值为 .
的值为 .
12.计算机执行以下程序:
①初始值![]() ;
;
②![]() ;
;
③![]() ;
;
④如果![]() ,则进行⑤,否则从②继续运行;
,则进行⑤,否则从②继续运行;
⑤打印![]() ;
;
⑥![]() 。
。
那么由语句⑤打印出的数值为 。
三、解答题:
13.已知函数![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,且
上是减函数,且![]() 的一个根为
的一个根为![]()
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证:![]() 还有不同于
还有不同于![]() 的实根
的实根![]() 、
、![]() ,且
,且![]() 、
、![]() 、
、![]() 成等差数列;
成等差数列;
(Ⅲ)若函数![]() 的极大值小于
的极大值小于![]() ,求
,求![]() 的取值范围。
的取值范围。
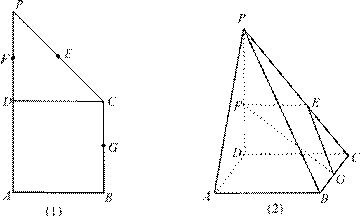
14.如图(1)在直角梯形![]() 中,
中,![]() ∥
∥![]()
![]() =2,
=2,![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的中点,现将
的中点,现将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() (如图2)
(如图2)
(1)求二面角![]() 的大小;
的大小;
(2)在线段![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ,并给出证明过程.
,并给出证明过程.
 |
15已知数列{an}(n∈N*),满足a1=1,a2=2,a3=3,a4=4,a5=5,当n≥5时,![]() ,若数列{bn}(n∈N*)满足
,若数列{bn}(n∈N*)满足![]() ,
,
(I)求b5;
(II)求证:当n≥5时,![]() ;
;
(III)求证:仅存在两个正整数m,使得![]() .
.
16.椭圆的中心是原点O,它的短轴长为![]() ,
,
相应于焦点F(c,0)(![]() )的准线
)的准线![]() 与
与![]() 轴
轴
相交于点A,OF=2FA,过点A的直线与
椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;
(2)若![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)设![]() (
(![]() ),过点P且平行于准线
),过点P且平行于准线![]() 的直线与椭圆相交于另一点M,
的直线与椭圆相交于另一点M,
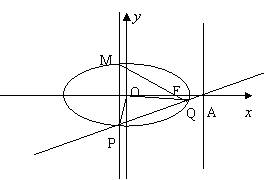 证明
证明![]() 。
。
答案
一. 选择题:
1)A 2)C 3)A 4)D 5)C 6)B 7)C 8)D
9)-252 10)![]()
![]() 11)
11)![]() 12)23
12)23
13.解:(Ⅰ)![]()
![]() 是极大值点,
是极大值点,![]()
(Ⅱ)令![]() ,得
,得![]() 或
或![]()
由![]() 的单调性知
的单调性知![]()
![]()
![]() 是方程
是方程![]() 的一个根,则
的一个根,则
![]()
![]()
![]()
方程![]() 的根的判别式
的根的判别式
![]()
又![]() ,
,
即![]() 不是方程
不是方程![]() 的根
的根
![]()
![]() 有不同于
有不同于![]() 的根
的根![]() 、
、![]() 。
。
![]()
![]() ,
,![]()
![]() 、
、![]() 、
、![]() 成等差数列
成等差数列
(Ⅲ)根据函数的单调性可知![]() 是极大值点
是极大值点
![]()
![]() ,于是
,于是![]()
令![]()
求导![]()
![]() 时,
时,![]()
![]()
![]() 在
在![]() 上单调递减
上单调递减
![]()
![]()
即![]()
14.取![]() 的中点
的中点![]() ,连
,连![]() 、
、![]() ,
,![]() ∥
∥![]() ,
,
![]() 又平面
又平面 ![]() 平面
平面![]() ,且
,且![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
由三垂线定理,得![]() ,
,
![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.
![]() 在
在![]() 中,
中,![]()
![]() ,即二面角
,即二面角![]() 的大小为
的大小为![]() .
.
(2)![]() 的中点时,有
的中点时,有![]()
![]() 平面
平面![]() .证明过程如下:
.证明过程如下:
![]() 为
为![]() 的中点,
的中点,![]() ∥
∥![]() ,又
,又![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,
从而![]() 、
、![]() 、
、![]() 、
、![]() 四点共面.
四点共面.
在![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,
又![]() 平面
平面![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,即
,即![]() 平面
平面![]() .
.

16.(1)解:由题意,可设椭圆的方程为![]() 。
。
由已知得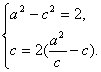
解得![]()
所以椭圆的方程为![]() ,离心率
,离心率![]() 。
。
(2)解:由(1)可得A(3,0)。
设直线PQ的方程为![]() 。由方程组
。由方程组
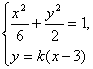
得![]()
依题意![]() ,得
,得![]() 。
。
设![]() ,则
,则
![]() , ①
, ①
![]() 。 ②
。 ②
由直线PQ的方程得![]() 。于是
。于是
![]() 。 ③
。 ③
∵![]() ,∴
,∴![]() 。 ④
。 ④
由①②③④得![]() ,从而
,从而![]() 。
。
所以直线PQ的方程为![]() 或
或![]() 。
。
(3)证明:![]() 。由已知得方程组
。由已知得方程组
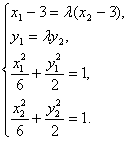
注意![]() ,解得
,解得![]()
因![]() ,故
,故![]()
![]() ,而
,而![]() ,
,
所以![]() 。
。