江苏省如东中学2007年高三数学试题2007.3。20
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,用时120分钟.
第Ⅰ卷(选择题,满分50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,把正确的代号填在指定位置上)
1.条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的
的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.若![]() ,则
,则![]() ,
,![]() ,
,![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
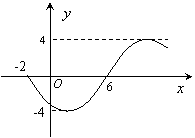 3.函数
3.函数![]() (
(![]() >0,
>0,![]() <
< ![]() ,
,![]() ∈R)的部分图象如图所示,则函数表达式为
∈R)的部分图象如图所示,则函数表达式为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.以抛物线![]() 上点
上点![]() 为切点的切线,与其准线交点的横坐标为
为切点的切线,与其准线交点的横坐标为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知正三棱锥S-ABC的三条侧棱两两互相垂直,且SA=2![]() ,则正三棱锥S-ABC的外接球的表面积是
,则正三棱锥S-ABC的外接球的表面积是
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.
![]()
6.设椭圆![]() 、双曲线
、双曲线![]() 、抛物线
、抛物线![]() (其中
(其中![]() )的离心率分别为
)的离心率分别为![]() ,则
,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 大小不确定
大小不确定
| 8 | 3 | 4 |
| 1 | 5 | 9 |
| 6 | 7 | 2 |
7.将![]() 个正整数
个正整数![]() 填入
填入![]() 方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做
方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做![]() 阶幻方.记
阶幻方.记![]() 为
为![]() 阶幻方对角线上数的和,如右图就是一个
阶幻方对角线上数的和,如右图就是一个![]() 阶幻方,可知
阶幻方,可知![]() .已知将等差数列:
.已知将等差数列:![]() 前
前![]() 项填入
项填入![]() 方格中,可得到一个
方格中,可得到一个![]() 阶幻方,则其对角线上数的和等于
阶幻方,则其对角线上数的和等于
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
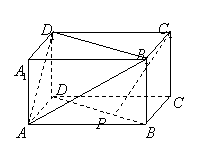
8.在长方体![]() 中,
中,![]() 为
为![]() 上任意一点,则一定有
上任意一点,则一定有
A.![]() 与
与![]() 异面
B.
异面
B.![]() 与
与![]() 垂直
垂直
C.![]() 与平面
与平面![]() 相交 D.
相交 D.![]() 与平面
与平面![]() 平行
平行
9.设![]() ,利用课本中推导等差数列前
,利用课本中推导等差数列前![]() 项和公式的方法,可求得
项和公式的方法,可求得![]() 的值为
的值为
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知奇函数![]() 的图象是两条直线的一部分(如图所示),其定义域为
的图象是两条直线的一部分(如图所示),其定义域为![]() ,则不等式
,则不等式![]() 的解集是
的解集是
A. ![]() B.
B. ![]()
C. ![]() D.
D.
![]()
第Ⅱ卷(非选择题,共计100分)
二、填空题(本大题共6小题,每小题5分,共30分,把正确的答案填在指定位置上)
11.若tan![]() =2,则2sin2
=2,则2sin2![]()
![]()
![]() sin2
sin2![]() =___________.
=___________.
12.若![]() (n∈N)的展开式中第3项为常数项,则展开式中二项式系数最大的是第____________项.
(n∈N)的展开式中第3项为常数项,则展开式中二项式系数最大的是第____________项.
13.在等比数列![]() 中,公比
中,公比![]() ,前99项的和
,前99项的和![]() ,则
,则![]() ______.
______.
14.在平面直角坐标系中,点A在圆![]() 上,点B在直线
上,点B在直线![]() 上,则线段AB的最小值= .
上,则线段AB的最小值= .
15.设![]() 为椭圆
为椭圆![]() 的焦点,过
的焦点,过![]() 且垂直于
且垂直于![]() 轴的直线与椭圆交于A,B两点,若△
轴的直线与椭圆交于A,B两点,若△![]() 为锐角三角形,则该椭圆离心率
为锐角三角形,则该椭圆离心率![]() 的取值范围是
.
的取值范围是
.
16.下面的语句是一个计算机程序的操作说明:
(1)初始值为![]() ;
;
(2)![]() (将当前
(将当前![]() 的值赋予新的
的值赋予新的![]() );
);
(3)![]() (将当前
(将当前![]() 的值赋予新的
的值赋予新的![]() );
);
(4)![]() (将当前
(将当前![]() 的值赋予新的
的值赋予新的![]() );
);
(5)![]() (将当前
(将当前![]() 的值赋予新的
的值赋予新的![]() );
);
(6)如果![]() ,则执行语句(7),否则返回语句(2)继续进行;
,则执行语句(7),否则返回语句(2)继续进行;
(7)打印![]() ;
;
(8)程序终止.
由语句(7)打印出的数值为_____________,_____________ .
三.解答题(本大题共5个小题,共70分).
17.(本题满分12分)
某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是0.5,0.6,0.9,且三门课程考试是否及格相互之间没有影响.求:
(Ⅰ)该应聘者用方案一考试通过的概率;
(Ⅱ)该应聘者用方案二考试通过的概率.
18.(本题满分14分)已知函数![]() .
.
(Ⅰ)若![]() 在
在![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() 是
是![]() 的极值点,求
的极值点,求![]() 在
在![]() 上的最小值和最大值.
上的最小值和最大值.
19. (本题满分14分)
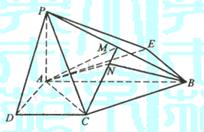
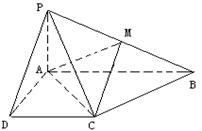 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,![]() 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=![]() AB=1,M是PB的中点。
AB=1,M是PB的中点。
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小。
20.(本题满分13分)函数![]() 的最小值为
的最小值为![]() 且
且![]() 数列
数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 是等差数列,且
是等差数列,且![]() ,求非零常数
,求非零常数![]() ;
;
(Ⅲ)若![]() ,求数列
,求数列![]() 的最大项.
的最大项.
21.(本题满分14分)
(1) 已知抛物线![]() 过焦点
过焦点![]() 的动直线l交抛物线于
的动直线l交抛物线于![]() 两点,
两点, ![]() 为坐标原点, 求证:
为坐标原点, 求证: ![]() 为定值;
为定值;
(2) 由 (1) 可知: 过抛物线的焦点![]() 的动直线 l 交抛物线于
的动直线 l 交抛物线于![]() 两点, 存在定点
两点, 存在定点![]() , 使得
, 使得
![]() 为定值. 请写出关于椭圆的类似结论,并给出证明.
为定值. 请写出关于椭圆的类似结论,并给出证明.
如东中学2007年高三数学模拟考试(3)参考答案
1.A 2.C 3.B 4.C 5.C 6.B 7.A 8.B 9.D 10.B
11.![]() 12.5 13.
12.5 13.![]() 14. 15.
14. 15. ![]() 16.
16. ![]()
17.解:记该应聘者对三门指定课程考试及格的事件分别为A,B,C,
则P(A)=0.5,P(B)=0.6,P(C)=0.9. - - -- - - - - - - - - - -2分
(Ⅰ) 应聘者用方案一考试通过的概率
p1=P(A·B·![]() )+P(
)+P(![]() ·B·C)+P(A·
·B·C)+P(A·![]() ·C)+P(A·B·C)
·C)+P(A·B·C)
=0.5×0.6×0.1+0.5×0.6×0.9+0.5×0.4×0.9+0.5×0.6×0.9
=0.03+0.27+0.18+0.27
=0.75. - - -- - - - - - - - - - -7分
(Ⅱ) 应聘者用方案二考试通过的概率
p2=![]() P(A·B)+
P(A·B)+![]() P(B·C)+
P(B·C)+ ![]() P(A·C)
P(A·C)
=![]() ×(0.5×0.6+0.6×0.9+0.5×0.9)
×(0.5×0.6+0.6×0.9+0.5×0.9)
=![]() ×1.29
×1.29
=0.43 - - -- - - - - - - - - - -12分
18.解:(Ⅰ) ![]() ,要
,要![]() 在
在![]() [1,+∞
[1,+∞![]() 上是增函数,则有
上是增函数,则有
![]() 在
在![]() [1,+∞
[1,+∞![]() 内恒成立,
内恒成立,
即![]() 在
在![]() [1,+∞
[1,+∞![]() 内恒成立, 又
内恒成立, 又![]() (当且仅当x=1时,取等号),所以
(当且仅当x=1时,取等号),所以![]()
(Ⅱ)由题意知![]() 的一个根为
的一个根为![]() ,可得
,可得![]() ,
,
所以![]() 的根为
的根为![]() 或
或 ![]() (舍去),
(舍去),
又![]() ,
,![]() ,
,![]() ,
,
∴ f(x)在![]() ,
,![]() 上的最小值是
上的最小值是![]() ,最大值是
,最大值是![]() .
.
19.本小题主要考查直线与平面垂直、直线与平面所成角的有关知识及思维能力和空间想象能力.考查应用向量知识解决数学问题的能力.满分14分.
|
(Ⅰ)证明:∵PA⊥面ABCD,CD⊥AD,
∴由三垂线定理得:CD⊥PD.
因而,CD与面PAD内两条相交直线AD,PD都垂直,
∴CD⊥面PAD.
又CD![]() 面PCD,∴面PAD⊥面PCD.
面PCD,∴面PAD⊥面PCD.
(Ⅱ)解:过点B作BE//CA,且BE=CA,
则∠PBE是AC与PB所成的角.
连结AE,可知AC=CB=BE=AE=![]() ,又AB=2,
,又AB=2,
所以四边形ACBE为正方形. 由PA⊥面ABCD得∠PEB=90°
在Rt△PEB中BE=![]() ,PB=
,PB=![]() ,
, ![]()
![]()
(Ⅲ)解:作AN⊥CM,垂足为N,连结BN.
在Rt△PAB中,AM=MB,又AC=CB,
∴△AMC≌△BMC,
∴BN⊥CM,故∠ANB为所求二面角的平面角.
∵CB⊥AC,由三垂线定理,得CB⊥PC,
在Rt△PCB中,CM=MB,所以CM=AM.
在等腰三角形AMC中,AN·MC=![]() ,
,
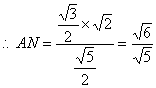 . ∴AB=2,
. ∴AB=2,![]()
故所求的二面角为![]()
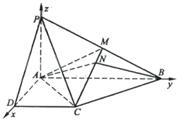
方法二:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为
A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,![]() .
.
(Ⅰ)证明:因![]()
由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.
|
(Ⅱ)解:因![]()
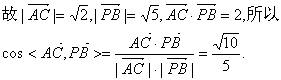
(Ⅲ)解:在MC上取一点N(x,y,z),则存在![]() 使
使![]()
![]()
要使![]()
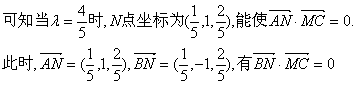
![]() 为所求二面角的平面角.
为所求二面角的平面角.
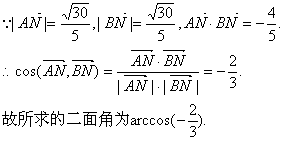
20.解:(Ⅰ)由![]()
![]()
![]() ,
,![]() ,
,![]()
由题意知:![]() 的两根,
的两根,
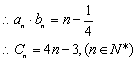
(Ⅱ)![]() ,
,![]()
![]()
![]()
![]() 为等差数列,
为等差数列,![]() ,
,![]() ,
,![]()
经检验![]() 时,
时,![]() 是等差数列,
是等差数列,![]()
(Ⅲ)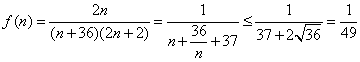

21. 23.(本小题满分14分)
解: (1) 若直线l垂直于x轴, 则![]() ,
, ![]() .
.
![]()
![]() ……………2分
……………2分
若直线l不垂直于轴, 设其方程为![]() ,
, ![]()
![]() .
.
由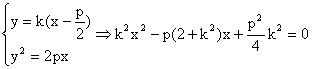
![]() ……………4分
……………4分
![]()
![]()
![]()
![]()
![]()
![]() .
.
综上, ![]()
![]() 为定值. ……………6分
为定值. ……………6分
(2) 关于椭圆有类似的结论: 过椭圆![]() 的一个焦点
的一个焦点![]() 的动直线l交椭圆于
的动直线l交椭圆于![]() 、
、![]() 两点, 存在定点
两点, 存在定点![]() , 使
, 使![]() 为定值. ……………7分
为定值. ……………7分
证明: 不妨设直线l过椭圆![]() 的右焦点
的右焦点![]()
![]() 其中
其中![]()
![]()
若直线l不垂直于轴, 则设其方程为: ![]() ,
, ![]()
![]() .
.
由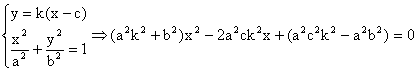 得:
得:
所以![]()
![]() ……………9分
……………9分
由对称性可知, 设点![]() 在x轴上, 其坐标为
在x轴上, 其坐标为![]()
所以![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
要使![]() 为定值,
为定值,
只要![]()
即![]()
此时![]()
![]()
![]()
![]() ……………12分
……………12分
若直线l垂直于x轴, 则其方程为![]() ,
, ![]() ,
, ![]() .
.
取点![]()
有![]()
![]()
![]()
![]() ……………13分
……………13分
综上, 过焦点![]() 的任意直线l交椭圆于
的任意直线l交椭圆于![]() 、
、![]() 两点, 存在定点
两点, 存在定点![]()
使![]()
![]() 为定值. ……………14分
为定值. ……………14分