2006-2007学年度上学期
高中学生学科素质训练
高三数学第一轮复习单元测试(1)— 《集合与函数》
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合![]() ,则满足
,则满足![]() 的集合B的个数是 ( )
的集合B的个数是 ( )
A.1 B.3 C.4 D.8
2.已知集合M={x![]() },N={yy=3x2+1,xÎR},则MÇN= ( )
},N={yy=3x2+1,xÎR},则MÇN= ( )
A.Æ B.{xx³1} C.{xx>1} D.{x x³1或x<0}
3.有限集合![]() 中元素个数记作card
中元素个数记作card![]() ,设
,设![]() 、
、![]() 都为有限集合,给出下列命题:
都为有限集合,给出下列命题:
①![]() 的充要条件是card
的充要条件是card![]() = card
= card![]() + card
+ card![]() ;
;
②![]() 的必要条件是card
的必要条件是card![]() card
card![]() ;
;
③![]() 的充分条件是card
的充分条件是card![]() card
card![]() ;
;
④![]() 的充要条件是card
的充要条件是card![]() card
card![]() .
.
其中真命题的序号是
A.③、④ B.①、② C.①、④ D.②、③
4.已知集合M={xx<3},N={xlog2x>1},则M∩N= ( )
A.![]() B.{x0<x<3} C.{x1<x<3} D.{x2<x<3}
B.{x0<x<3} C.{x1<x<3} D.{x2<x<3}
5.函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.函数![]() 的定义域是 ( )
的定义域是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.下列函数中,在其定义域内既是奇函数又是减函数的是 ( )
A.![]() B.
B.![]()
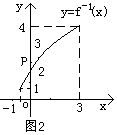 C.
C.![]() D.
D.![]()
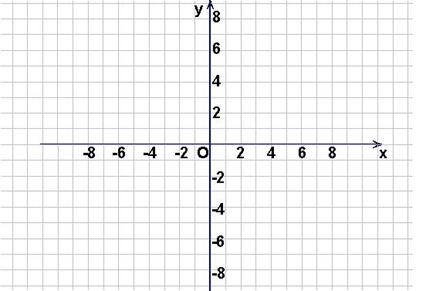
8.函数![]() 的反函数
的反函数![]() 的图象与y轴交于点
的图象与y轴交于点
![]() (如图2所示),则方程
(如图2所示),则方程![]() 的根是
的根是![]() ( )
( )
A.4 B.3 C.2 D.1
9.已知函数![]() 若
若![]() 则
( )
则
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 与
与![]() 的大小不能确定
的大小不能确定
10.为确保信息安全,信息需加密传输,发送方由明文![]() 密文(加密),接收方由密文
密文(加密),接收方由密文![]() 明文(解密),已知加密规则为:明文
明文(解密),已知加密规则为:明文![]() 对应密文
对应密文![]() 例如,明文
例如,明文![]() 对应密文
对应密文![]() 当接收方收到密文
当接收方收到密文![]() 时,则解密得到的明文为 ( )
时,则解密得到的明文为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.如图所示,单位圆中弧AB的长为x,f(x)表示弧AB与弦AB所
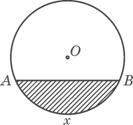 围成的弓形面积的2倍,则函数y=f(x)的图象是( )
围成的弓形面积的2倍,则函数y=f(x)的图象是( )
|
12.关于![]() 的方程
的方程![]() ,给出下列四个命题:
,给出下列四个命题:
①存在实数![]() ,使得方程恰有2个不同的实根;
,使得方程恰有2个不同的实根;
②存在实数![]() ,使得方程恰有4个不同的实根;
,使得方程恰有4个不同的实根;
③存在实数![]() ,使得方程恰有5个不同的实根;
,使得方程恰有5个不同的实根;
④存在实数![]() ,使得方程恰有8个不同的实根.
,使得方程恰有8个不同的实根.
其中假命题的个数是 ( )
A.0 B.1 C.2 D.3
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
13.函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() 则
则![]() _______.
_______.
14.设f(x)=log3(x+6)的反函数为f-1(x),若〔f-1(m)+6〕〔f-1(n)+6〕=27,则f(m+n)=___________________.
15.设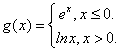 则
则![]() __________.
__________.
16.设![]() ,则
,则![]() 的定义域为_____________ .
的定义域为_____________ .
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知函数![]() 满足
满足![]() 且对于任意
且对于任意![]() , 恒有
, 恒有![]() 成立.
成立.
(1)求实数![]() 的值;
的值;
(2)解不等式![]() .
.
18(本小题满分12分)
20个下岗职工开了50亩荒地,这些地可以种蔬菜、棉花、水稻,如果种这些农作物每亩地所需的劳力和预计的产值如下:
| 每亩需劳力 | 每亩预计产值 | |
| 蔬 菜 |
| 1100元 |
| 棉 花 |
| 750元 |
| 水 稻 |
| 600元 |
问怎样安排,才能使每亩地都种上作物,所有职工都有工作,而且农作物的预计总产值达到最高?
19.(本小题满分12分)
已知函数![]()
![]()
(1)若![]() 且函数
且函数![]() 的值域为
的值域为![]() ,求
,求![]() 的表达式;
的表达式;
(2)在(1)的条件下, 当![]() 时,
时, ![]() 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设![]() ,
, ![]()
![]() 且
且![]() 为偶函数, 判断
为偶函数, 判断![]() +
+![]() 能否大于零?
能否大于零?
20.(满分12分)
已知定义域为R的函数f(x)满足f(f(x)-x2+y_=f(x)-x2+x.
(1)若f(2)-3,求f(1);又若f(0)=a,求f(a);
(2)设有且仅有一个实数x0,使得f(x0)= x0,求函数f(x)的解析表达式.
21.(本小题满分12分)
设函数![]() .
.
(1)在区间![]() 上画出函数
上画出函数![]() 的图像;
的图像;
(2)设集合![]() . 试判断集合
. 试判断集合![]() 和
和![]() 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的
图像的
上方.
22.(本小题满分14分)
设a为实数,记函数![]() 的最大值为g(a).
的最大值为g(a).
(1)设t=![]() ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);
(2)求g(a);
(2)试求满足![]() 的所有实数a.
的所有实数a.
参考答案(1)
1.C.![]() ,
,![]() ,则集合B中必含有元素3,即此题可转化为求集合
,则集合B中必含有元素3,即此题可转化为求集合![]() 的子集
的子集
个数问题,所以满足题目条件的集合B共有![]() 个.故选择答案C.
个.故选择答案C.
2.C.M={xx>1或x£0},N={yy³1}故选C
3.B.选由card![]() = card
= card![]() + card
+ card![]() + card
+ card![]() 知card
知card![]() = card
= card![]() +
+
card![]()
![]() card
card![]() =0
=0![]()
![]() .由
.由![]() 的定义知card
的定义知card![]() card
card![]() .
.
4.D. ![]() ,用数轴表示可得答案D.
,用数轴表示可得答案D.
5.A.∵ ![]() ∴
∴![]() 即
即![]()
∵![]() ∴
∴![]() 即
即![]()
∴函数![]() 的反函数为
的反函数为![]() .
.
6.B.由![]() ,故选B.
,故选B.
7.B.在其定义域内是奇函数但不是减函数;C在其定义域内既是奇函数又是增函数;D在其定义域内不是奇
函数,是减函数;故选A.
8.C.利用互为反函数的图象关于直线y=x对称,得点(2,0)在原函数![]() 的图象上,即
的图象上,即![]() ,
,
所以根为x=2.故选C
9. B.取特值![]() ,选B;或二次函数其函数值的大小关系,分类研究对
,选B;或二次函数其函数值的大小关系,分类研究对
成轴和区间的关系的方法, 易知函数的对成轴为![]() ,开口向上的抛物线, 由
,开口向上的抛物线, 由![]() , x1+x2=0,需
, x1+x2=0,需
分类研究![]() 和对成轴的关系,用单调性和离对成轴的远近作判断,故选B;
和对成轴的关系,用单调性和离对成轴的远近作判断,故选B;
10.B.理解明文![]() 密文(加密),密文
密文(加密),密文![]() 明文(解密)为一种变换或为一种对应关系,构建方程组求解,依提意用明文表示密文的变换公式为
明文(解密)为一种变换或为一种对应关系,构建方程组求解,依提意用明文表示密文的变换公式为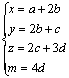 ,于是密文14,9,23,28满足,即有
,于是密文14,9,23,28满足,即有 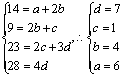 ,选B;
,选B;
11.D.当x=![]() 时,阴影部分面积为
时,阴影部分面积为![]() 个圆减去以圆的半径为腰的等腰直角三角形的面积,故此时
个圆减去以圆的半径为腰的等腰直角三角形的面积,故此时![]() ,即点(
,即点(![]() )在直线y=x的下方,故应在C、D中选;而当x=
)在直线y=x的下方,故应在C、D中选;而当x=![]() 时, ,阴影部分面积为
时, ,阴影部分面积为![]() 个圆加上以圆的半径为腰的等腰直角三角形的面积,即
个圆加上以圆的半径为腰的等腰直角三角形的面积,即![]()
![]() ,即点(
,即点(![]() )在直线y=x的上方,故选D.
)在直线y=x的上方,故选D.
12.B.本题考查换元法及方程根的讨论,要求考生具有较强的分析问题和解决问题的能力;据题意可令![]()
![]() ①,则方程化为
①,则方程化为![]() ②,作出函数
②,作出函数![]() 的图象,结合函数的图象可知:(1)当t=0或t>1时方程①有2个不等的根;(2)当0<t<1时方程①有4个根;(3)当t=1时,方程①有3个根.
的图象,结合函数的图象可知:(1)当t=0或t>1时方程①有2个不等的根;(2)当0<t<1时方程①有4个根;(3)当t=1时,方程①有3个根.
故当t=0时,代入方程②,解得k=0此时方程②有两个不等根t=0或t=1,故此时原方程有5个根;当方程②有两个不等正根时,即![]() 此时方程②有两根且均小于1大于0,故相应的满足方程
此时方程②有两根且均小于1大于0,故相应的满足方程![]() 的解有8个,即原方程的解有8个;当
的解有8个,即原方程的解有8个;当![]() 时,方程②有两个相等正根t=
时,方程②有两个相等正根t=![]() ,相应的原方程的解有4个;故选B.
,相应的原方程的解有4个;故选B.
13.由![]() 得
得![]() ,所以
,所以![]() ,则
,则![]() .
.
14.f-1(x)=3x-6故〔f-1(m)+6〕·〔f-1(x)+6〕=3m·3n=3m +n=27
\m+n=3\f(m+n)=log3(3+6)=2.
15.![]() .
.
16.由![]() 得,
得,![]() 的定义域为
的定义域为![]() 。故
。故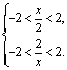 ,解得
,解得![]() .
.
故![]() 的定义域为
的定义域为![]() .
.
17. (1) 由![]() 知,
知, ![]() …① ∴
…① ∴![]() …②又
…②又![]() 恒成立, 有
恒成立, 有![]() 恒成立,故
恒成立,故![]() .
.
将①式代入上式得:![]() , 即
, 即![]() 故
故![]() .
.
即![]() , 代入② 得,
, 代入② 得,![]() .
.
(2)![]()
![]() 即
即![]() ∴
∴![]()
解得: ![]() , ∴不等式的解集为
, ∴不等式的解集为![]() .
.
18.设种蔬菜、棉花、水稻分别为x亩,y亩,z亩,总产值为u,
依题意得x+y+z=50,![]() ,则u=1100x+750y+600z=43500+50x.
,则u=1100x+750y+600z=43500+50x.
∴ x![]() 0,y=90-3x
0,y=90-3x![]() 0,z=wx-40
0,z=wx-40![]() 0,得20
0,得20![]() x
x![]() 30,∴当x=30时,u取得大值43500,此时y=0,z=20.
30,∴当x=30时,u取得大值43500,此时y=0,z=20.
∴安排15个职工种30亩蔬菜,5个职工种20亩水稻,可使产值高达45000元.
19 (1) ∵![]() , ∴
, ∴![]() 又
又![]() 恒成立,
恒成立,
∴![]() , ∴
, ∴![]() ,
, ![]() ∴
∴![]() .
.
∴![]()
(2) 则![]()
![]() ,
,
当![]() 或
或![]() 时, 即
时, 即![]() 或
或![]() 时,
时,
![]() 是单调函数.
是单调函数.
(3) ∵![]() 是偶函数∴
是偶函数∴![]()
![]() ,
,
∵![]() 设
设![]() 则
则![]() .又
.又![]()
∴![]()
![]() +
+![]()
![]() ,∴
,∴![]() +
+![]() 能大于零.
能大于零.
20.(1)因为对任意xεR,有f(f(x)- x2 + x)=f(x)- x2 +x,所以f(f(2)- 22+2)=f(2)- 22+2.
又由f(2)=3,得f(3-22+2)-3-22+2,即f(1)=1.
若f(0)=a,则f(a-02+0)=a-02+0,即f(a)=A.
(2)因为对任意xεR,有f(f(x))- x2 +x)=f(x)- x2 +x.
又因为有且只有一个实数x0,使得f(x0)- x0. 所以对任意xεR,有f(x)- x2 +x= x0.
在上式中令x= x0,有f(x0)-x![]() + x0= x0, 又因为f(x0)- x0,所以x0- x
+ x0= x0, 又因为f(x0)- x0,所以x0- x![]() =0,故x0=0或x0=1.
=0,故x0=0或x0=1.
若x0=0,则f(x)- x2 +x=0,即f(x)= x2 –x. 但方程x2 –x=x有两上不同实根,与题设条件矛质,
故x2≠0. 若x2=1,则有f(x)- x2 +x=1,即f(x)= x2 –x+1.易验证该函数满足题设条件.
综上,所求函数为f(x)= x2 –x+1(x![]() R).
R).
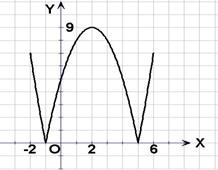 21.(1)
21.(1)
(2)方程![]() 的解分别是
的解分别是![]() 和
和![]() ,
,
由于![]() 在
在![]() 和
和![]() 上单调递减,
上单调递减,
在![]() 和
和![]() 上单调递增,因此
上单调递增,因此
![]() .
.
由于![]() .
.
(3)[解法一] 当![]() 时,
时,![]() .
. ![]()
![]()
![]() ,
,
![]()
![]() . 又
. 又![]() ,
,
① 当![]() ,即
,即![]() 时,取
时,取![]() ,
,
![]()
![]() .
.
![]() ,
则
,
则![]() .
.
② 当![]() ,即
,即![]() 时,取
时,取![]() ,
, ![]() =
=![]() .
.
由 ①、②可知,当![]() 时,
时,![]() ,
,![]() .
.
因此,在区间![]() 上,
上,![]() 的图像位于函数
的图像位于函数![]() 图像的上方.
图像的上方.
[解法二] 当![]() 时,
时,![]() .
.
由![]() 得
得![]() ,
,
令 ![]() ,解得
,解得 ![]() 或
或![]() ,
,
在区间![]() 上,当
上,当![]() 时,
时,![]() 的图像与函数
的图像与函数![]() 的图像只交于一点
的图像只交于一点![]() ;
;
当![]() 时,
时,![]() 的图像与函数
的图像与函数![]() 的图像没有交点.
的图像没有交点.
如图可知,由于直线![]() 过点
过点![]() ,当
,当![]() 时,直线
时,直线![]() 是由直线
是由直线
![]() 绕点
绕点![]() 逆时针方向旋转得到. 因此,在区间
逆时针方向旋转得到. 因此,在区间![]() 上,
上,![]() 的图像
的图像
位于函数![]() 图像的上方.
图像的上方.
22.(1)∵![]() ,∴要使
,∴要使![]() 有意义,必须
有意义,必须![]() 且
且![]() ,即
,即![]()
∵![]() ,且
,且![]() ……① ∴
……① ∴![]() 的取值范围是
的取值范围是![]() 。
。
由①得:![]() ,∴
,∴![]()
![]() ,
,![]() 。
。
(2)由题意知![]() 即为函数
即为函数![]()
![]() ,
,![]() 的最大值,
的最大值,
∵直线![]() 是抛物线
是抛物线![]()
![]() 的对称轴,∴可分以下几种情况进行讨论:
的对称轴,∴可分以下几种情况进行讨论:
1)当![]() 时,函数
时,函数![]() ,
,![]() 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由![]() 知
知![]() 在
在![]() 上单调递增,故
上单调递增,故![]()
![]()
![]() ;
;
2)当![]() 时,
时,![]() ,
,![]() ,有
,有![]() =2;
=2;
3)当![]() 时,,函数
时,,函数![]() ,
,![]() 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若![]()
![]() 即
即![]() 时,
时,![]()
![]() ,
,
若![]()
![]() 即
即![]() 时,
时,![]()
![]() ,
,
若![]()
![]() 即
即![]() 时,
时,![]()
![]()
![]() .
.
综上所述,有![]() =
=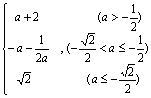 .
.
(3)当![]() 时,
时,![]()
![]()
![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,∴
,∴![]() ,
,
![]()
![]() ,故当
,故当![]() 时,
时,![]()
![]() ;
;
当![]() 时,
时,![]() ,由
,由![]()
![]() 知:
知:![]()
![]() ,故
,故![]() ;
;
当![]() 时,
时,![]() ,故
,故![]() 或
或![]() ,从而有
,从而有![]() 或
或![]() ,
,
要使![]()
![]() ,必须有
,必须有![]() ,
,![]() ,即
,即![]() ,
,
此时,![]()
![]() 。
。
综上所述,满足![]() 的所有实数a为:
的所有实数a为:![]() 或
或![]() .
.