2007届高三文科数学模拟题
武穴中学
一..选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在等比数列![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知函数![]() 在区间[1,2]上的最大值比最小值大2,则
在区间[1,2]上的最大值比最小值大2,则![]() 的值为( )
的值为( )
(A)2
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.若向量![]() =
=![]()
![]() =(1,-1),则2
=(1,-1),则2![]() 的取值范围是( )
的取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)[1,3]
(D)[1,3]
4.函数![]() 的反函数是( )
的反函数是( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
5.![]() 的展开式中存在常数项,则n的值可以是( )
的展开式中存在常数项,则n的值可以是( )
(A)12 (B)13 (C)11 (D)10
6.小李进行射击训练,每次射中目标的概率为![]() ,且各次射击相互没有影响,则他射击5次恰好命中3次且恰有2次连续命中的概率为
,且各次射击相互没有影响,则他射击5次恰好命中3次且恰有2次连续命中的概率为
A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7. 在坐标平面上,不等式组![]() 所表示的平面区域的面积为( )
所表示的平面区域的面积为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)2
(D)2
8. 若动点(![]() )在曲线
)在曲线![]() 上变化,则
上变化,则![]() 的最大值为 ( )
的最大值为 ( )
A.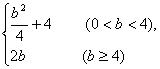 B.
B.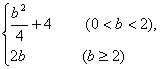 C.
C.![]() D.2
D.2![]()
9. 点O是三角形ABC所在平面内的一点,满足![]() ,则点O是
,则点O是![]() 的( )
的( )
(A)三个内角的角平分线的交点 (B)三条边的垂直平分线的交点 (C)三条中线的交点 (D)三条高的交点
10.若一个圆的圆心在抛物线![]() 的焦点处,且此圆与直线
的焦点处,且此圆与直线![]() 相切,则这个圆的方程是 ( )
相切,则这个圆的方程是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题(本题共4小题,每小题5分,共25分)
11.若指数函数![]() 的部分对应值如下表:
的部分对应值如下表:
|
| -2 | 0 | 2 |
|
| 0.694 | 1 | 1.44 |
 则不等式
则不等式![]() 的解集为 。
的解集为 。
12.用6种不同的颜色给图中的“笑脸”涂色,要求“眼睛”(即图中A、B所示区域)用相同颜色,则不同的涂法共有_________种。(用数字作答)
13. 已知椭圆的中心为坐标原点O,焦点在![]() 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,![]() 与
与![]() =(3,1)共线。
=(3,1)共线。
则椭圆的离心率为 。
14.已知函数![]() ,数列
,数列![]() 的通项公式是
的通项公式是![]() (
(![]() ),当
),当
![]() 取得最小值时,
取得最小值时,![]() .
.
15..已知![]() 其中b>2a,则不等式
其中b>2a,则不等式![]() --------
--------
三、解答题:(本大题共6小题,共75分)
16. (本小题满分12分) 已知![]() 。
。
(1)求![]() 的值;(2)求
的值;(2)求![]() 的值。
的值。
17(本小题满分10分)武穴中学对其网络服务器开放的4个外网络端口的安全进行监控,以便在发现黑客入侵时及时跟踪锁定。根据跟踪调查发现,这4个网络端口各自受到黑客入侵的概率为0.1,求(1)恰有3个网络端口受到黑客入侵的概率是多少?(2)至少有2个网络端口受到黑客入侵的概率是多少?
18.(本题满分14分)
设函数![]() …,是公差为2的等差数列,且x1=a4
…,是公差为2的等差数列,且x1=a4
(1)求数列![]() 的通项公式;
的通项公式;
(2)![]() ;
;
(3)令![]()
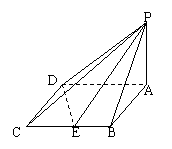
19.(本小题满分12分)如图四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD = 60°,PA⊥平面ABCD,设E为BC的中点,二面角P-DE-A为45°.
(1 ) 求点A到平面PDE的距离;
(2 ) 在PA上确定一点F,使BF∥平面PDE;
(3 ) 求异面直线PC与DE所成的角(用反三角函数表示);
(4 ) 求面PDE与面PAB所成的不大于直二面角的二面角的大小(用反三角函数表示).
 |
20. (本小题满分13分)
已知抛物线C∶x2 = 8y,焦点为F,准线与y轴交于点A,过A且斜率为k的直线l与抛物线C交于P、Q两点.
(1)求满足![]() 的点R的轨迹方程;
的点R的轨迹方程;
(2)若∠PFQ为钝角,求直线l的斜率k的取值范围.
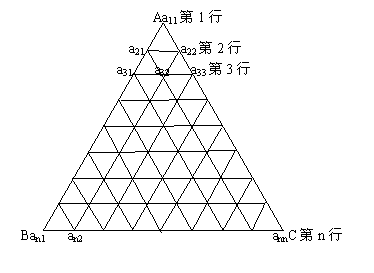
21.(14分)如图,把正△ABC分成有限个全等的小正三角形,且在每个小三角形的顶点上都放置一个非零实数,使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等。设点A为第1行,…,BC为第n行,记点A上的数为![]() 第i行中左起第j个数为
第i行中左起第j个数为![]() 若
若![]()
(1)求![]() ;
;
(2)试归纳出![]() 的表达式(用含n,m的式子表示,不必证明);
的表达式(用含n,m的式子表示,不必证明);
 (3)记
(3)记![]() ,证明
,证明![]()
文科数学答案
一.CDABC CBADA
二.11)(0,1)U(1,2)
12) 216
13) ![]() 14)110
15)
14)110
15) ![]()
三.16. 解:(1)![]()
![]()
![]() ………………6分
………………6分
(2)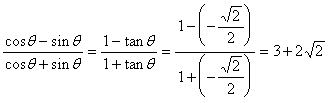 ………………12分
………………12分
17. 解:(1)![]() ………………4分
………………4分
(2)“至少有2个网络端口被入侵”的对立事件为“没有和有1个网络端口被入侵”,因此![]() ………10分
………10分
18. 解:(1)![]()
![]()
(2)由![]() 知:是以
知:是以![]() 为首项,a2为公比等比数列
为首项,a2为公比等比数列
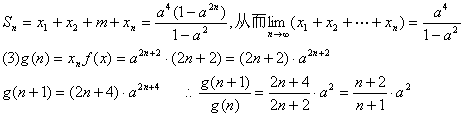
![]()
19.(1)DE为正△BCD的中线,DE⊥BC,∴DE⊥AD,又PA⊥平面ABCD,DE⊥PD,∠PDA = 45°,作AH⊥PD于H,则DE⊥AH,∴AH⊥平面PDE,PA = AD = 2,
AH =![]() ,即点A到平面PDE的距离为
,即点A到平面PDE的距离为![]() 。
。
(2)F为PA的中点,可证BF∥EH,∴BF∥平面PDE。
(3)延长AD到G,使DG = EC,连CG、PG,可证CG∥DE,△PCG中,CG =![]()
PC =![]() PG =
PG =![]() PC与DE所成角为
PC与DE所成角为![]()
(4)设![]() 连PM,作HO⊥PM于O,连AO,可证∠AOH为所求二面角的平面角,AO =
连PM,作HO⊥PM于O,连AO,可证∠AOH为所求二面角的平面角,AO =![]()
20. 解:(1) ∵C∶x 2 = 8 y ∴焦点F(0,2),准线:![]() ,则A(0,-2)··········· 1分
,则A(0,-2)··········· 1分
由已知可设:l∶![]() ,R(x,y),P(x1,y1),Q(x2,y2)··············· 1分
,R(x,y),P(x1,y1),Q(x2,y2)··············· 1分
将l代C整理得:![]() ······························································· 1分
······························································· 1分
由![]() ,···································································· 1分
,···································································· 1分
又由韦达定理:
x1 + x2
= 8 k,x1 x2 = 16,![]() ···························· 1分
···························· 1分
又∵![]() =(x,y-2),
=(x,y-2),![]() =(x1,y1-2),
=(x1,y1-2),![]() =(x2,y2-2)
=(x2,y2-2)
∴由![]() (x,y-2)=(x1 + x2,y1 + y2-4)
(x,y-2)=(x1 + x2,y1 + y2-4)
即![]() ,······································································ 1分
,······································································ 1分
消去K得R的轨迹方程:x2 = 8(y + 6)(y > 2)········································· 2分
(2) ∵∠PFQ为钝角 ∴![]() ·
·![]() <0 即
<0 即![]() ··············· 2分
··············· 2分
![]() ······························································ 2分
······························································ 2分
![]() 1分
1分
21. (1)![]() ,
,![]()
(2)![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]()
![]() 是公比为
是公比为![]() 的等比数列,
的等比数列,![]()
(3)由(2)知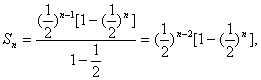
![]()
又![]()
![]()