江西省宜春市2007届高三第三次模拟考试数学(理科)试题 4月22日
命题人:吴连进(高安教育集团)熊星飞(宜丰中学)李希亮 审校人:李希亮 胡鸿(宜春中学)
I 卷
(注意:请将第Ⅰ卷答案填在第Ⅱ卷上)
一、选择题:(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合![]() ,
,![]() ,则
,则![]() 与
与![]() 的关系为( )
的关系为( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.命题![]() :不等式
:不等式![]() 的解集为
的解集为![]() ,命题
,命题![]() :在△
:在△![]() 中,“
中,“![]() ”是“
”是“![]() ”成立的必要非充分条件,则( )
”成立的必要非充分条件,则( )
A. ![]() 真
真![]() 假 B.
假 B.![]() 且
且![]() 为真 C.
为真 C.![]() 或
或![]() 假 D.
假 D.![]() 假
假![]() 真
真
3.等式“![]() ”成立是“
”成立是“![]() 、
、![]() 、
、![]() 成等差数列”的( )
成等差数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
4.若函数![]() 对任意
对任意![]() 都有
都有
![]() ,则
,则![]() ( )
( )
A.8 B.4 C. -4 D.-4或4
5.设![]() 是正实数,以下不等式:
是正实数,以下不等式:![]() ;
;![]() ;
;![]() ;
;
![]() ,其中恒成立的有:
,其中恒成立的有:
A.![]()
![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
![]()
6.等差数列![]() 中,若
中,若![]() ,新数列
,新数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() 的值为( )
的值为( )
A.14 B. 15 C.16 D.18
7.已知△![]() 的顶点
的顶点![]() 在椭圆
在椭圆![]() 上,顶点
上,顶点![]() 是椭圆的一个焦点,且椭圆的另一个焦点在边
是椭圆的一个焦点,且椭圆的另一个焦点在边![]() 上,则△
上,则△![]() 的周长为( )。
的周长为( )。
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.![]() 为奇函数,
为奇函数,![]() 则
则![]() ( )
( )
A.0 B.1
C.![]() D.5
D.5
9.当太阳斜照或直照时,放在水平地面上的长方体箱子,在地面上影子的形状是( )
A.四边形或五边形 B.四边形或六边形
C.五边形或六边形 D.四边形或五边形或六边形
10.在1,2,3,4,5的排列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,中,满足
,中,满足 ![]() ,
, ![]() ,
,![]() ,
, ![]() 的排列个数是( )
的排列个数是( )
A.10 B.12 C.14 D.16
11.下列函数图象无论经过平移还是关于某条直线对称翻折后仍不能与![]() 的图象重合的是( )
的图象重合的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.在正三棱锥![]() 中,
中,![]() 、
、![]() 分别为棱
分别为棱![]() 、
、![]() 的中点,且
的中点,且![]() ,
,![]() ,则此三棱锥
,则此三棱锥![]() 外接球的表面积为( )
外接球的表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本题共4小题,每小题4分,共16分)
13.己知复数![]() 满足
满足![]() ,则
,则![]() 。
。
14.已知![]() 为实数,
为实数,![]() ,
,![]() ,那么
,那么![]() 与
与![]() 的关系为 。
的关系为 。
15.己知![]() 满足
满足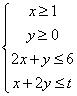 ,其中实数
,其中实数![]() ,则目标函数
,则目标函数![]() 的最大值的变化范围是
。
的最大值的变化范围是
。
16.![]() 、
、![]() 是双曲线
是双曲线![]() 右支上的两点,若弦
右支上的两点,若弦![]() 的中点到
的中点到![]() 轴的距离是4,则
轴的距离是4,则![]() 的最大值是 。
的最大值是 。
宜春市2007届高三年级第三次模拟考试数学(理科)试题
Ⅱ卷
(注意:请将第Ⅰ卷答案填在此卷上)
一、选择题:(本题共12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(本题共4小题,每小题4分,共16分)
13. 14.
15. 16.
 三、解答题(本大题共6小题,共74分,解答写出必要的文字说明,注明过程及演算步骤)
三、解答题(本大题共6小题,共74分,解答写出必要的文字说明,注明过程及演算步骤)
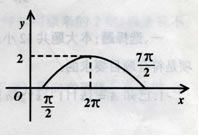
17.(本小题满分12分) 如右图所示,已知函数![]()
![]() 的一部分图象.
的一部分图象.
(1)求![]() 的值,讨论函数在
的值,讨论函数在![]() 上的单调性;
上的单调性;
(2)![]() ,且
,且![]() ,求证:
,求证:![]() 。
。
18.(本小题满分12分)根据某地区的高考录取情况统计:高考录取中,上线考生第一次被录取的概率为![]() ;若第一次未被录取,则通过补报志愿,第二次被录取的概率为
;若第一次未被录取,则通过补报志愿,第二次被录取的概率为![]() 。
。
求:(1)在高考录取中某上线学生被录取的概率为多少?
(2)若某小组有5位同学上线,则这5位同学中第一次就有4人被录取的概率为多少?
(假设学生之间的录取是相互独立的)
(3)在条件(2)中,5位上线同学被录取人数的期望是多少?
19.(本小题满分12分)已知斜三棱柱![]() 的底面是直角三角形,
的底面是直角三角形,![]() ,侧棱与底面所成的角为
,侧棱与底面所成的角为![]() ,点
,点![]() 在底面上的射影
在底面上的射影![]() 落在
落在![]() 上.
上.
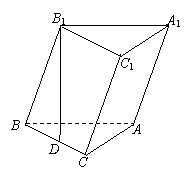 (1)求证:
(1)求证:![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 且
且![]() 恰为
恰为![]() 中点?
中点?
(3)若![]() ,且
,且![]() 时,求二面
时,求二面
角![]() 的大小.
的大小.
20.(本题满分12分)设函数![]()
(1)求![]() 的单调区间;
的单调区间;
(2)若当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数![]() 的取值范围.
的取值范围.
21.(本小题满分12分)已知![]() 是抛物线
是抛物线![]() 的任一弦,
的任一弦,![]() 为抛物线的焦点,
为抛物线的焦点,![]() 为准线.
为准线.![]() 为过
为过![]() 点且以
点且以![]() 为方向向量的直线.
为方向向量的直线.
(1)若过![]() 点的抛物线的切线与
点的抛物线的切线与![]() 轴相交于
轴相交于![]() 点,求证:
点,求证:![]() ;
;
(2 )若![]() (
(![]() 、
、![]() 异于原点),直线
异于原点),直线![]() 与
与![]() 相交于点
相交于点![]() ,试求点
,试求点![]() 的轨迹方程;
的轨迹方程;
(3)若![]() 为焦点弦,分别过
为焦点弦,分别过![]() 、
、![]() 点的抛物线的两条切线相交于点
点的抛物线的两条切线相交于点![]() , 求证:
, 求证:![]() ,且
,且![]() 点在l上.
点在l上.
22.(本小题满分14分)已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ;等比数列
;等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)若对于任意![]() ,总存在
,总存在![]() ,使
,使![]() ,求
,求![]() 的值;
的值;
(3)在(2)中,记![]() 是
是![]() 中所有满足
中所有满足![]() 的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记![]() 为
为![]() 的前n项和,
的前n项和,![]() 为
为![]() 的前n项和,求证:
的前n项和,求证:
![]() ≥
≥![]()
![]() .
.
宜春市2007届高三年级第三次模拟考试
数学(理科)试题参考答案及评分标准
一、选择题:(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(本题共4小题,每小题4分,共16分)
13. ![]() 14.
14.![]() 15.
15.![]() 16.8
16.8
三、解答题(本大题共6小题,共74分,解答写出必要的文字说明,注明过程及演算步骤)
17.(1)由题意得![]() . 当
. 当![]() 时,
时,![]() 的最大值
的最大值![]() 与最小值
与最小值![]() 互为相反数,设
互为相反数,设![]() 的最小正周期为
的最小正周期为![]() ,由图知
,由图知![]() ,
,
得![]() .又
.又![]() ,
, ![]() ,于是
,于是![]() ,得
,得![]() .
.
这时,![]() ,它经过两点
,它经过两点![]() ,
, ![]() 得
得
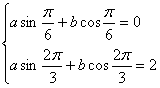 有
有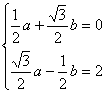 ,解之,得
,解之,得![]()
所以![]() ,
,![]() ……………………………………………4分
……………………………………………4分
得![]() =
= ![]() sin
sin![]() x-cos
x-cos![]() x=2sin(
x=2sin(![]() x-
x-![]() ),所以
),所以![]() 在
在![]() 上单调递减;在
上单调递减;在![]() 上单调递增.……………………………………………………6分
上单调递增.……………………………………………………6分
(2) 当![]() 时,讨论
时,讨论![]() 的取值:
的取值:
①若![]() ,由
,由![]() ,
,![]() 在
在![]() 上单调递减,得
上单调递减,得![]() ;
;
②若![]() 时,则
时,则![]() ……10分
……10分
当![]() 时,
时,![]() ,
,![]()
综上所述,![]() ……………………………………………………12分
……………………………………………………12分
18.解:(1)记事件![]() :上线考生第一次被录取
:上线考生第一次被录取
记事件![]() :上线考生第一次未被录取,补报志愿第二次被录取
:上线考生第一次未被录取,补报志愿第二次被录取
依题意,得:![]()
![]() …………3分
…………3分
显然事件![]() 与事件
与事件![]() 是互斥事件
是互斥事件
所以 ![]() ……………6分
……………6分
(2)依题意,知:5位上线同学第一次有3人被录取的概率
![]() ………………………………9分
………………………………9分
(3)因为每位上线同学中,最后被录取的概率为![]() ,且同学之间被录取与否是相互独立的,所以5位上线学生中被录取的人数
,且同学之间被录取与否是相互独立的,所以5位上线学生中被录取的人数![]() ……10分
……10分
所以![]() …………………………………………12分
…………………………………………12分
19.解:(1)∵ ![]() ,
, ![]()
∴![]()
∴ ![]() ………………………… 3分
………………………… 3分
(2) ∵![]() ,要使
,要使![]() ,由三垂线定理可知,
,由三垂线定理可知,
只须![]() ………………………… 5 分
………………………… 5 分
∴ 平行四边形![]() 为菱形, 此时,
为菱形, 此时,![]() .
.
又∵ ![]() , 要使
, 要使![]() 为
为![]() 中点,只须
中点,只须![]() ,即△
,即△![]() 为正三角形,
为正三角形,
∴ ![]() ………………………… 7分
………………………… 7分
∵ ![]() ,且
,且![]() 落在
落在![]() 上,
上,
∴![]() 即为侧棱与底面所成的角.
即为侧棱与底面所成的角.
故当![]() 时,
时,![]() ,且使
,且使![]() 为
为![]() 中点 ……………………… 8分
中点 ……………………… 8分
(3)过![]() 作
作![]() 于
于![]() ,则
,则![]() 。
。
过![]() 作
作![]() 于
于![]() ,由三垂线定理,得
,由三垂线定理,得![]()
∴![]() 是所求二面角
是所求二面角![]() 的平面角. …………………… 10分
的平面角. …………………… 10分
设![]() ,
,
在![]() 中,由
中,由![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]()
![]() a.
a.
∴![]() ,故所求的二面角
,故所求的二面角![]() 为
为![]() .……………… 12分
.……………… 12分
20.解:(I)函数定义域为![]() ,
,
因为![]() ……………………………2分
……………………………2分
由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() 或
或![]() .
.
所以递增区间是![]() ,递减区间是
,递减区间是![]() ………………4分
………………4分
(2)由(1)知,![]() 在
在![]() 上递减,在
上递减,在![]() 上递增. 又
上递增. 又![]() ,
,
![]() ,且
,且![]() ,所以
,所以![]() 时,
时,
![]() ……………………………………………………………………6分
……………………………………………………………………6分
故![]() 时,不等式
时,不等式![]() 恒成立.…………………………………………8分
恒成立.…………………………………………8分
(III)方程![]() ,即:
,即:![]() . 记
. 记![]()
所以![]() . 由
. 由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得:
,得:
![]() . 所以
. 所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,为使
上递增,为使![]() 在
在![]() 上恰好有两个相异的实根,必须且只需
上恰好有两个相异的实根,必须且只需![]() 在
在![]() 和
和![]() 上各有一个实根,于是
上各有一个实根,于是
有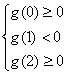 ,解之,得
,解之,得![]() .……………………12分
.……………………12分
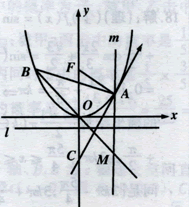
21.(1)如图所示,设![]() ,易知点
,易知点![]() 即为切点. ∵
即为切点. ∵![]() ,∴
,∴![]() ,于是
,于是![]() 的方程为:
的方程为:![]() ,即:
,即:![]() ,
, 
令![]() ,得
,得![]()
即![]() 由抛物线的定义可知,
由抛物线的定义可知,
![]() .
又
.
又![]()
∴![]() .………………………………………………………………4分
.………………………………………………………………4分
(2)设![]() ,∵
,∵![]() ·
·![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() . 直线
. 直线![]() 的方程:
的方程:![]() …… ①
…… ①
…………………………………………………………………………………6分
直线![]() 的方程:
的方程:![]() ………②,①×②,得
………②,①×②,得![]() ,∴
,∴![]()
∵![]() , ∴
, ∴![]() ,
,
∴![]() 点的轨迹方程为
点的轨迹方程为![]() .……………………………………………8分
.……………………………………………8分
(3)设![]() ,易知
,易知![]() 、
、![]() 为切点,则
为切点,则![]()
由于![]() 是焦点弦,可设
是焦点弦,可设![]() 的方程为:
的方程为:![]() ,代入
,代入![]() ,
,
得:![]() ,
,
∴![]() , ∴
, ∴![]() ,∴
,∴![]() .………………………10分
.………………………10分
由(1)知,![]() 的方程:
的方程:![]() ,
,
∴![]() ,即:
,即:![]() . 又∵
. 又∵![]() 过焦点,
过焦点,
∴![]() ,∴
,∴![]() ,∴
,∴![]() 点在准线
点在准线![]() 上.…………………………12分
上.…………………………12分
22.解:(1)∵ ![]() ,
,![]() ,
,![]() ,
,
∴ ![]() ∴
∴ 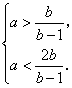 ∴
∴ 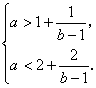
∴ ![]() .…………………………………………………………3分
.…………………………………………………………3分
∴ a=2或a=3
当a=3时,![]() ;不符合
;不符合![]() ,舍去 ∴a=2.……………4分
,舍去 ∴a=2.……………4分
(2)![]() ,
,![]() ,由
,由![]() 可得
可得
![]() . ∴
. ∴ ![]() .
.
∴ b=5………………………………………………………………8分
(3)由(2)知![]() ,
,![]() , ∴
, ∴ ![]() .
.
∴ ![]() . ∴
. ∴ ![]() ,
,![]() .
.
∵ ![]() ,
,![]() .…………………………………10分
.…………………………………10分
当n≥3时,
![]()
![]()
![]()
![]() .
.
∴ ![]() . 综上得
. 综上得 ![]()
![]() .………………14分
.………………14分