江西省南昌市第二中学
高三第二次数学（理）统考试题
赖 敬 华
2006. 9. 26.
一，选择题（12
5=60）
1已知集合
{
}，
{
}，下列法则不能构成
到
的映射是（ ）
2不等式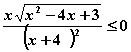
的解集是（ ）
{
}
{且
} {
且或
=1 或=3}
{
且或=1 或=3}
3若
，则下列不等式中成立的是 （ ）
4设
{
}，
{
}，若
则实数
的取值范围（ ）
5设
是实数，则
是“
的（ ）
充分不必要条件，
充分必要条件 
必要不充分条件，，既不充分也不必要条件
6已知
，则
的值为（ ）
7已知
则函数
的值蜮为（ ）
8不等式
的解集是（ ）
9设是实数，
则
的最小值是（ ）
10已知
，则
的值域是（ ）
11已知定义在
上的奇函数
在区间
上是增函数，若
的内角满足
则的取值范围（ ）
12当
不等式
恒成立，则实数的取值范围（ ）
， 
二填空题
13若
则
----------------
14若不等式
的解集是
且
则实数的取值范围是：----------------
15若不等式
在
范围内恒成立，则实数
的取值范围是：-------------------
16平面上点
满足
则
的最小值：—————
三解答题
17（12分）已知
求（1）
的值。（2）
的值。
18（12分）已知函数
若不等式
在
上恒成立，求实数的取值范围。
19（12分）设是定义在
上的奇函数，若
时有
（1） 用定义证明在上是增函数；（2）解不等式：
20（12分）已知函数的导数
满足
常数
为方程
的实数根。
（1） 求证：当
时，总有
成立。
（2） 对任意
满足
求证：
21（12分）已知函数
（1）
若
求证：
（2）
若不等式
，
时，恒成立，求实数的取值范围。
22(14分)设
是函数
（
的一个极大值点，
（1）求实数的取值范围。（2）求的增区间。
（3）设
若存在
使得
成立。
求实数的取值范围。
高三（理）答案
一、CDCCA，CDCAB，DC
二、13 — 
14 
15 
16 
三、解答题部分
17、（1）
+
=
=
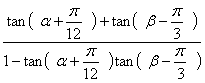
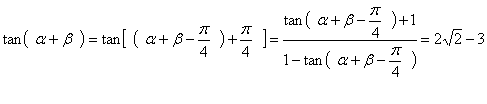
18、解：
在[1、4]上恒成立。
设
即
在[1，2]上恒成立
设
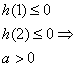
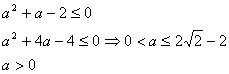
19、（1）证明：任取
，则：
由已知
即
在[-1，1]上为增函数
（2）在[-1，1]上为增函数
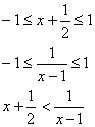解得
20、证明：（1）令
为增函数
又
当
时，
即
(2)不妨设
为增函数，即
令
)
所以
为减函数，即
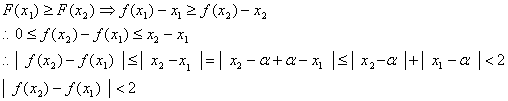
方法2
（1）
点
两点的斜率为
根据导数的几何意义，存在一点
使得
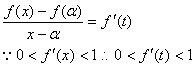
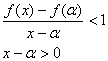
当
不等式显然成立
当
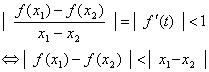
又
综上得
21、（1）设
在
上是增函数
所以
既成立。
（2）原不等式等价于
令
令
列表如下：
| x | -1 | (-1,0) | 0 | (0,1) | 1 |
|
| 0 | + | 0 | — | 0 |
|
| 极小值 |
| 极大值 | ↘ | 极小值 |
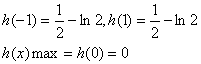
当
时，
令
,则
在[-1，1]为非负正数
得
或
22、解：
令
则
|
|
|
|
| 3 |
|
|
| - | 0 | + | 0 | - |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ |
（1）
时， 函数取得极大值
时，
即
时,
即 即
↗
而所求的
的取值范围是
,
（2）由（1）知在
上是增函数。
（3）当
故在[0、3]上为增函数。
故在[0、3]上的值域为
而
在[0、3]上为增函数，所以
的值域为
=
由假设知
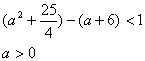
故的取值范围是：（
）