江苏省淮安市2006![]() 2007学年度高三第二次调查测试模拟试数学试题
2007学年度高三第二次调查测试模拟试数学试题
命题人:黄涛 2006.1.20
(本卷满分150分,考试时间120分钟)
第I卷(选择题,满分50分)
一.选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题意要求的)
1、已知集合![]() 集合
集合![]() 则
则![]() 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2、若![]() 的展开式中含有常数项,则这样的正整数
的展开式中含有常数项,则这样的正整数![]() 的最小值是
的最小值是
A. 3 B.4 C. 10 D. 12
3、设![]() 是两条不同的直线,
是两条不同的直线,![]() 是两个不同的平面,则下列四个命题:
是两个不同的平面,则下列四个命题:
①若a⊥b,a⊥![]() ,则b∥
,则b∥ ![]() ②若a∥
②若a∥![]() ,
,![]() ⊥β,则a⊥β
⊥β,则a⊥β
③a⊥β,![]() ⊥β,则a∥
⊥β,则a∥![]() ④若a⊥b,a⊥
④若a⊥b,a⊥![]() ,b⊥β,则
,b⊥β,则![]() ⊥β
⊥β
其中正确的命题的个数是 ( )
A.0个 B.1个 C.2个 D.3个
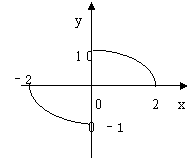
4、如图,函数![]() 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在![]() 轴上的椭圆的两段弧,则不等式
轴上的椭圆的两段弧,则不等式
![]() 的解集为
( )
的解集为
( )
 A、
A、![]()
B、![]()
C、![]()
D、![]()
5、数列![]() 满足
满足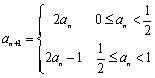 若
若![]() 则
则![]() 的值为
( )
的值为
( )
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
6、由函数![]() 与函数
与函数![]() 的图象及
的图象及![]() 与
与![]() 所围成的封闭图形的面积是
( )
所围成的封闭图形的面积是
( )
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
7、设命题![]() : 在直角坐标平面内,点
: 在直角坐标平面内,点![]() 与
与![]() 在直线
在直线
![]() 的异侧;命题
的异侧;命题![]() :若向量
:若向量![]() 满足
满足![]() ,则
,则![]() 的夹角为锐角.以下结论正确的是
( )
的夹角为锐角.以下结论正确的是
( )
A.![]() 为真,
为真, ![]() 为真 B.
为真 B.![]() 为真,
为真, ![]() 为假
为假
C.![]() 为假,
为假, ![]() 为真 D.
为真 D.![]() 为假
为假 ![]() 为假
为假
8、将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体高的最小值为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、已知点A(1,0),B(1,),将线段OA、AB各n等分,设OA上从左至右的第k个分点为Ak,AB上从下至上的第k个分点为Bk(1≤k≤n),过点Ak且垂直于x轴的直线为lk,OBk交lk于Pk,则点Pk在同一 ( )
A.圆上 B.椭圆上 C.双曲线上 D.抛物线上
10、已知C为线段AB上一点,P为直线AB外一点,满足![]() ,
,![]() ,
,![]() ,I为PC上一点,且
,I为PC上一点,且![]()
![]() ,则
,则![]() 的值为( )
的值为( )
A
1
B 2
C.![]() D
D ![]()
第Ⅱ卷(非选择题,共100分)
二、填空题(本大题共6小题,每小题5分,共30分.把答案填写在答题卡相应位置上.)
11、已知![]() ,则
,则![]() ________▲________.
________▲________.
12、已知直线ax+by+c=0被圆M:![]() 所截得的弦AB的长为
所截得的弦AB的长为![]() ,那么
,那么![]() 的值等于 ▲
的值等于 ▲ ![]()
13、过双曲线M:![]() 的左顶点A作斜率为1的直线
的左顶点A作斜率为1的直线![]() ,若
,若![]() 与双曲线M的两条渐近线分别相交于B、C,且AB=BC,则双曲线M的离心率是 ▲
与双曲线M的两条渐近线分别相交于B、C,且AB=BC,则双曲线M的离心率是 ▲
14、4位同学参加某种形式的竞赛,竞赛规则规定:每位同学必须从甲、乙两道题中任选
一题作答,选甲题答对得18分,答错得-18分;选乙题答对得6分,答错得-6分.若4
位同学的总分为0,则这4位同学不同得分情况的种数是 ▲
15、对于函数![]() 给出下列命题:
给出下列命题:
(1)![]() 有最小值; (2)当
有最小值; (2)当![]() 时,
时,![]() 的值域为
的值域为![]() ;
;
(3)当![]() 时,
时,![]() 在
在![]() 上有反函数;
上有反函数;
(4)若![]() 在区间
在区间![]() 上是增函数,则实数
上是增函数,则实数![]() 的取值范围是
的取值范围是![]() .
.
上述命题中正确的是_____▲________.(填上所有正确命题的序号)
16、定义:设有限集合![]() ,
,![]() ,则
,则![]() 叫做集合
叫做集合![]() 的模,记作
的模,记作![]() .若集合
.若集合![]() ,集合
,集合![]() 的含有三个元素的全体子集分别为
的含有三个元素的全体子集分别为![]() ,则
,则![]() = ▲ (用数字作答).
= ▲ (用数字作答).
三、解答题(本大题共5小题,共70分. 解答应写出文字说明,证明过程或演算步骤.)
17、(本题12分)已知点A、B、C的坐标分别为A(3,0),B(0,3),C(cosα,sinα),
![]() 求:
求:
(1)若![]() ,求角α的值;
,求角α的值;
| |
(2)若![]() ,求
,求![]() 的值.
的值.
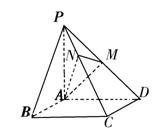 18、(本题12分)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,且PA=AD=2,点M、N分别在棱PD、PC上,且
18、(本题12分)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,且PA=AD=2,点M、N分别在棱PD、PC上,且![]()
(1)求证:PC⊥AM:
(2)求证:PC⊥平面AMN;
(3)求二面角B-AN-M的大小.
19、(本题14分)某厂生产某种产品的年固定成本为![]() 万元,每生产
万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() ,当年产量不足
,当年产量不足![]() 千件时,
千件时,![]() (万元);当年产量不小于
(万元);当年产量不小于![]() 千件时,
千件时,![]() (万元).通过市场分析,若每件售价为
(万元).通过市场分析,若每件售价为![]() 元时,该厂年内生产该商品能全部销售完.
元时,该厂年内生产该商品能全部销售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
20、(本题16分)在直角坐标系中,O为坐标原点,F是x轴正半轴上的一点,若△OFQ的面积为S,且![]() .
.
(Ⅰ)若![]() 夹角θ的取值范围;
夹角θ的取值范围;
(Ⅱ)设![]() 若以O为中心,F为焦点的椭圆经过点Q,求
若以O为中心,F为焦点的椭圆经过点Q,求![]() 的最小值以及此时的椭圆方程;
的最小值以及此时的椭圆方程;
| |
21、(本题16分)设函数![]() 的定义域、值域均为
的定义域、值域均为![]() ,
,![]() 的反函数为
的反函数为![]() ,且对于任意实数
,且对于任意实数![]() ,均有
,均有![]() ,定义数列
,定义数列![]() :
:![]() .
.
(1)求证:![]() ;
;
(2)设![]() 求证:
求证:![]() ;
;
(3)是否存在常数![]() ,同时满足:①当
,同时满足:①当![]() 时,有
时,有![]() ;② 当
;② 当![]() .时,有
.时,有![]() 成立.如果存在满足上述条件的实数
成立.如果存在满足上述条件的实数![]() ,求出
,求出![]() 的值;如果不存在,证明你的结论。
的值;如果不存在,证明你的结论。
淮安市2006![]() 2007学年度高三年级第二次调查测试模拟试
2007学年度高三年级第二次调查测试模拟试
数学卷答题纸
|
| |||||||||||||||||||||||||
| 一、选择题:
| |||||||||||||||||||||||||
| | |||||||||||||||||||||||||
| 第Ⅱ卷 非选择题 (共100分) | |||||||||||||||||||||||||
| 二、填空题: 11题 12题 | |||||||||||||||||||||||||
|
13题 14题 | |||||||||||||||||||||||||
| 15题 16题 | |||||||||||||||||||||||||
| 三、解答题 17、(本小题满分12分)
18、(本小题满分12分)
19、(本小题满分14分)
20、(本小题满分16分)
21、(本小题满分16分)
|
淮安市2006![]() 2007学年度高三年级第二次调查测试模拟试卷
2007学年度高三年级第二次调查测试模拟试卷
参考答案
| 第Ⅰ卷 选择题 (共50分) | |||||||||||||||||||||||||
| 一、选择题:
|
二、填空题
11、 ![]() 12、 -2
13、
12、 -2
13、 ![]()
14、 44 15、 (2)(3) 16、 3600
三、解答题
17、解:解:(1)∵![]() =(cos
=(cos![]() -3, sin
-3, sin![]() ),
), ![]() =(cos
=(cos![]() ,
sin
,
sin![]() -3).
-3).
∴∣![]() ∣=
∣=![]() 。
。
∣![]() ∣=
∣=![]() 。------------------------3分
。------------------------3分
由∣![]() ∣=∣
∣=∣![]() ∣得sin
∣得sin![]() =cos
=cos![]() .又∵
.又∵![]()
![]() ,∴
,∴![]() =
=![]() -----------6分
-----------6分
(2)由![]() ·
·![]() =-1,得(cos
=-1,得(cos![]() -3)cos
-3)cos![]() +sin
+sin![]() (sin
(sin![]() -3)=-1
-3)=-1
∴ sin![]() +cos
+cos![]() =
=![]() .① 又
.① 又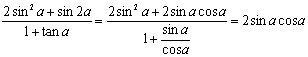 .
.
由①式两边平方得1+2sin![]() cos
cos![]() =
=![]() , ----------------------------------10分
, ----------------------------------10分
∴2sin![]() cos
cos![]() =
=![]() , ∴
, ∴![]() ---------------------12分
---------------------12分
18、解: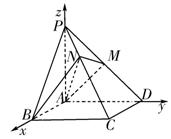 (1)因为四棱锥P—ABCD的底面是正方形,PA⊥底面ABCD,故建立如图所示的空间直角坐标A-xyz,又PA=AD=2,则有P(0,2,2),D(0,2,0).∴M(0,1,1),C(2,2,0).
(1)因为四棱锥P—ABCD的底面是正方形,PA⊥底面ABCD,故建立如图所示的空间直角坐标A-xyz,又PA=AD=2,则有P(0,2,2),D(0,2,0).∴M(0,1,1),C(2,2,0).
∴![]() =(2,2,-2),
=(2,2,-2),![]() =(0,1,1).
=(0,1,1).
∵![]() ·
·![]() =0+2-2=0,∴PC⊥AM.
=0+2-2=0,∴PC⊥AM.
(2)设N(x,y,z),
∵![]() =
=![]() ,则有x-0=
,则有x-0=![]() ,
,
∴![]() 同理可得
同理可得![]()
由![]() ·
·![]() =
=![]() ∴PC⊥AN.又∵PC⊥AM,AM
∴PC⊥AN.又∵PC⊥AM,AM![]() ∴PC⊥平面AMN.
∴PC⊥平面AMN.
(3)设平BAN的法向量为n(x,y,z).由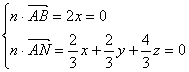 ,取n(0,2,1).
,取n(0,2,1).
而![]() =(2,2,-2)为平面AMN的法向量,
=(2,2,-2)为平面AMN的法向量,
∴cos<n,![]() >
>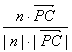 =
=![]() =-
=-![]()
结合图形可知,所求二面角B-AN-M的大小为π-arccos![]()
19、解:(1)当![]() 时,
时,
![]()
……………………3分
当![]() ,
,![]() 时,
时,
![]()
……6分
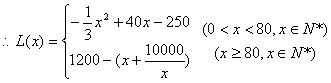 …………………7分
…………………7分
(2)当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 取得最大值
取得最大值![]() …………………10分
…………………10分
当![]()
![]()
![]() 当
当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() …13分
…13分
综上所述,当![]() 时
时![]() 取得最大值
取得最大值![]() ,即年产量为
,即年产量为![]() 千件时,该厂在这一商品的生产中所获利润最大. …………………14分
千件时,该厂在这一商品的生产中所获利润最大. …………………14分
20、解:(I)由已知得![]()
![]()
(II)设椭圆的方程是![]() ,Q点的坐标设为(x1,y1),
,Q点的坐标设为(x1,y1),
则![]() ∵△OFQ的面积是
∵△OFQ的面积是![]()
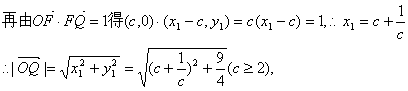
显然当且权当c=2时![]() 有最小值,其最小值是3,
有最小值,其最小值是3,
此时Q点的坐标是 ![]() ,代入椭圆方程是
,代入椭圆方程是![]() ,
,
解得a2=10,b2=6,∴所求椭圆方程是![]() .
.
(III)由(II)椭圆方程![]() ,椭圆的左焦点为F1(-2,0),
,椭圆的左焦点为F1(-2,0),
欲求M点到右准线距离的最大值,可求该点到左准线距离的最小值,设A、B、
M点在左准线的射影分别为A′、B′、M′,由椭圆第二定义及梯形中位线性质得:
![]()
由![]()
即M点到左准线距离的最小值为2,此时A、F1、B三点共线,
设过F1的直线方程为x=hy-2,将其与椭圆方程联立,
消去x得(3h2+5)y2-12hy-18=0,
∴y1+y2=![]() ,此时中点M的纵坐标为y0=
,此时中点M的纵坐标为y0=![]() ,
,
故得M点的横坐标为x0=![]() -2,
-2, 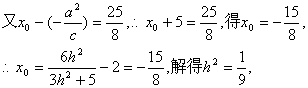
∴所求的直线方程为x=![]() y-2,即3x-y+2=0或3x+y+2=0.
y-2,即3x-y+2=0或3x+y+2=0.
21、.解:(1)由![]() ,得
,得![]() ,
,
又![]()
![]() ,令
,令![]() 得
得
![]() ,即
,即![]() ;---------------------------------4分
;---------------------------------4分
(2)![]() ,
,![]() ,即
,即![]() ,---------6分
,---------6分
又![]() ,
,
所以![]() ,
,
所以![]() -----------8分
-----------8分
(3)假设存在常数![]() ,使得当
,使得当![]() 时,有
时,有![]() ,则
,则![]() ,解得
,解得![]() 。
---------------------------10分
。
---------------------------10分
由![]() ,即
,即![]() ,
,
两边同时除以![]() ,得
,得![]() ,分别令
,分别令![]() 得
得
![]() ,
,![]() ,
,![]()
![]() ,--------13分
,--------13分
将这![]() 个不等式想加得
个不等式想加得![]()
![]() 。
。
即存在![]() ①当
①当![]() 时,有
时,有![]() ;
;
② 当![]() .时,有
.时,有![]() 成立.----------------------------16分
成立.----------------------------16分
 第Ⅰ卷 选择题 (共50分)
第Ⅰ卷 选择题 (共50分)