浙江省杭州市
2007年高三第二次高考科目教学质量检测
数学试题（文科）
考生须知：
1．本卷满分150分，考试时间120分钟。
2．答题前，在答题卷密封区内填写学校、班级和姓名。
3．所有答案必须写在答题卷上，写在试题卷上无效。
4．考试结束，只需上交答题卷。
参考公式：
如果事件A，B互斥，那么 P(A+B)=P(A)+P(B)；
如果事件A、B相互独立，那么 P(A·B)=P(A)·P(B)；
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
一、选择题（本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的。）
1．设集合A={1，2，a}，B={1，a2}，若A∪B=A，则实数a的可能取值有 （ ）
A．2个 B．3个 C．4个 D．5个
|
的图象是下图中的 （ ）
3．若
，则一定有 （ ）
A．a与 b共线 B．a⊥b
C．a与 b的夹角为45° D．a=b
4．若
的展开式中只有第4项的系数最大，那么这个展开式中的常数项是（ ）
A．15 B．35 C．30 D．20
5．椭圆4
的准线方程为 （ ）
A．x=
B．x=
C．y== D．y=
6．下列不等式中，解集不是空集的是 （ ）
A．x2+(1－x)2≤0 B．x2－3x+2≤x2－x+1
C．x2+9<6x D．3x2－2x+1<0
7．设a,b,c是空间三条直线，α，β是空间两个平面，则下列命题中，逆命题不成立的是（ ）
A．当c⊥α时，若c⊥β，则α//β
B．当b
α时，若b⊥β，则α⊥β
C．当bα时，且c是a在α内的射影时，若b⊥c，则a⊥b
D．当bα时，且c
α时，若c//α，则b//c
|
=0是f(x)在x0处取得极值的 （ ）
A．充分但不必要的条件 B．必要但不充分的条件
C．充分必要条件 D．既不充分也不必要的条件
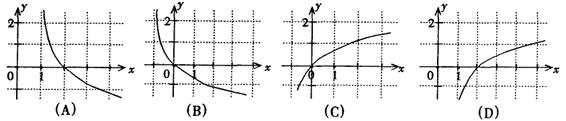
9．设函数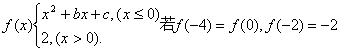
，则关于x的方程f(x)=x
解的个数为 （ ）
A．4个 B．3个 C．2个 D．1个
10．在O点测量到远处有一物体在作等速直线运动，开始时该物体位于P点，一分钟后，其位置在Q点，且∠POQ=90°，再过一分钟后，该物体位于R点，且∠QOR=30°，则tan2∠OPQ的值等于 （ ）
A．
B．
C．
D．
二、填空题：本大题有7小题，每小题4分，共28分.把答案填在答题卷的相应位置上。
11．一个容量为n的样本，分成若干组，已知某组的频数和频率分别为40和0.125，则n的值为 .
12．设x∈Z，则函数
的值域是
.
13．在数列{an}中，a1=－60，且an+1=an+3，则这个数列的前30项的绝对值之和为 .
14．已知实数
的最
值是 .
15．圆心在抛物线 
的焦点且与其准线相切的圆方程是
.
|
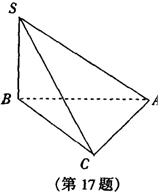
17．三棱锥S—ABC中，∠SBA=∠SCA=90°，
△ABC是斜边AB=a的等腰直角三角形，
则以下结论中：①异面直线SB与AC所
成的角为90°；②直线SB⊥平面ABC；
③面SBC⊥面SAC；④点C到平面SAB的
距离是
a.其中正确结论的序号是
.
三、解答题：本大题有5小题，18至21每小
题14分，22题16分，共72分。解答应写
出文字说明，证明过程或演算步骤。
|
设函数
（1）求f(x)的最小正周期T；
（2）求f(x)的单调递增区间.
19．（本小题满分14分）
（1）请写出一个各项均为实数且公比q∈（0，1）的等比数列，使得其同时满足a1+a6=11
且
；
（2）在符合（1）条件的数列中，能否找到一正偶数m，使得
这三个数依次
成等差数列？若能，求出这个m的值；若不能，请说明理由.
20．（本小题满分14分）
某人口袋中有人民币50元3张，20元3张和10元4张.
（1）现从中任意取出若干张，求总数恰好等于80元的不同取法种数（用数字作答）；
（2）现从中任意取出3张，求总数超过80元的概率.
|
|
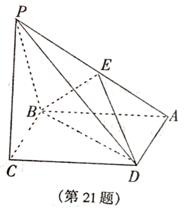
已知四棱锥P——ABCD的底面是边长为a
的菱形，∠ABC=120°，又PC⊥平面ABCD，
PC=a，E是PA的中点.
（1）求证：平面EBD⊥平面ABCD；
（2）求直线PB与直线DE所成的角的余弦值；
（3）设二面角A—BE—D的平面角为θ，
求cosθ的值.
22．（本小题满分16分）
|
，
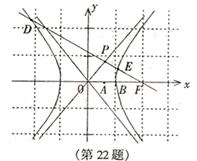
B是右顶点，F是右焦点，点A在x正半轴上，
且满足
成等比数列.过F作
双曲线C在一三象限的渐近线的垂直l，垂足为P.
（1）求证：
；
（2）若l与双曲线C的左右两支分别相交于点D，E，求双曲线C的离心率e的取值范围.
参考答案
一、选择题：（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | A | B | D | C | D | B | D | B | C |
二、填空题：（本大题共7小题，每小题4分，共28分）
11．320
12．
13．765
14．大；0
15．(x+2)2+y2=16
|
17．①②③④
三、解答题：（本大题有5小题，18至21每小题14分，22题16分，共72分）
18．（本小题满分14分）
……4分
（1）最小正周期
………………………………………………4分
（2）由
，
所以f(x)的单调递增区间是 
.……………………6分
19．（本小题满分14分）
（1）由条件可知a1，a6应该是方程
的两个根，
解得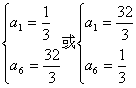 
，继而得到q=2或q=，………………4分
所以符合条件的等比数列可以是
（公比q>1舍去），…………3分
若
，符合条件…………………………3分
（2）若存在符合题设要求的正整数m，
对于
，
由
，可解得m=7（舍去），………………………………2分
或m=6符合题意.…………………………………………………………2分
20．（本小题满分14分）
（1）分①取1张50元1张20元张10元；②取1张50元3张10元；③取3张20元2
张10元；④取2张2 …………………………………………………………4分
所以不同取法的种数共有
；………………3分
（2）分①取3张50元；②取2张50元1张20元；③取2张50元1张10元；④取1
张50元2张20元四种情况，…………………………………………4分
可求得
.……………………3分
21．（本小题满分14分）
|
∵ABCD的底面是边长为a的菱形，
∠ABC=120°，PC=a，E是PA的中点.所以
C（0，0，0），A（0，
a，0），
B（－a，a，0），D（a，a，0），
P（0，0，a），
∵E是PA的中点，
∴E（0，a，a）.……………………2分
（1）设 AC和BD交于点Q，则Q（0，a，0），
，PC⊥平面ABCD，∴QP⊥平面ABCD；平面EBD
⊥平面ABCD； ……………………4分
（2）
，
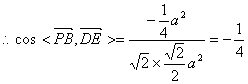；…………………………………4分
（3）设平面的ABE的法向量为p（x，y，z），可得p=（－，1，），
又AC⊥BC，得AC⊥面BDE，又
=（0，a，0），
∴取平面BDE的法向量q=（0，，0），
∴p·q=，p=
，q=
∴
…………………………………………4分
22．（本小题满分16分）
（1）设
与渐近线
联立，解得
…………2分
由成等比数列，可得A
………………2分
所以
，………………2分
可证得
……………………………………2分
（2）设与双曲线方程联立，消去y，得到
，…………………………3分
由韦达定理
……3分
所以e2>2，得到离心率的范围为e>
.……………………………………2分