2006-2007学年度上学期
高中学生学科素质训练
高三数学第一轮复习单元测试—期末试卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(理)若复数![]() 的值为
( )
的值为
( )
A.i B.1 C.-1 D.-i
(文)关于![]() 的函数
的函数![]() 的极值点的个数有
( )
的极值点的个数有
( )
A.2个
B.1个
C.0个
D.由![]() 确定
确定
2.设集合![]() ,
,![]() ,则
,则![]() 中元素的个数是
( )
中元素的个数是
( )
A.0 B.1 C.2 D.1或2
3.平面α与球O相交于周长为2π的⊙O′,A、B为⊙O′上两点,若∠AOB=![]() ,且A、B的球面距为
,且A、B的球面距为![]() 则OO′的长度为 ( )
则OO′的长度为 ( )
A.1
B.![]() C.π
D.2
C.π
D.2
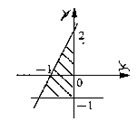
4.图中阴影部分可用哪一组二元一次不等式表示 ( )
 A.
A.![]() B.
B.![]()
C.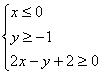 D.
D.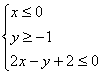
5.在下列命题中,真命题是 ( )
A.直线![]() 都平行于平面
都平行于平面![]() ,则
,则![]()
B.设![]() 是直二面角,若直线
是直二面角,若直线![]() ,则
,则![]()
C.若直线![]() 在平面
在平面![]() 内的射影依次是一个点和一条直线,且
内的射影依次是一个点和一条直线,且![]() ,则
,则![]() 或
或![]()
D.设![]() 是异面直线,若
是异面直线,若![]() 平面
平面![]() ,则
,则![]() 与
与![]() 相交
相交
6.(理)已知椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 和
和![]() .若
.若![]() 是
是![]() 的等比中项,
的等比中项,![]() 是
是![]() 与
与![]() 的等差中项,则椭圆的离心率是 ( )
的等差中项,则椭圆的离心率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
(文)已知双曲线的一条准线与两渐近线的交点分别为![]() 、
、![]() ,相应于这条准线的焦点为
,相应于这条准线的焦点为![]() ,如果
,如果![]() 是等边三角形,那么双曲线的离心率为
( )
是等边三角形,那么双曲线的离心率为
( )
A.2
B.![]() C.4
D.
C.4
D.![]()
7.曲线y=2sin(x + )cos(x -)和直线y= 在y轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则P2P4等于 ( )
A .π B .2π C. 3π D .4π
8.(理)设可导函数![]() 是R上的奇函数,
是R上的奇函数,![]() ,且当x<0时,
,且当x<0时,![]() ,则不等式
,则不等式![]() 的解集是
( )
的解集是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(文)设函数![]() 是R上的偶函数,对于任意的
是R上的偶函数,对于任意的![]() 都有
都有![]() ,且
,且![]() ,则
,则![]() ( )
( )
A.3 B.-3 C.2 D.2006
9.设![]() ,函数
,函数![]() ,则函数
,则函数![]() 的
的![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.某人获悉一个岛上三处藏有宝物.由于年代久远,有的数据缺失,记载如下:岛上有一棵椰子树,由叶子树向东走3米为藏宝处A,继续向东走b米,到达B处然后向东偏北60°走a米为藏宝处C(其中a,b为缺少数据),由B向南走![]() 为藏宝处E,三个藏宝处在以B为焦点,椰子树的南北方向所在直线为相应的准线的双曲线上.寻宝的关键是推出a,b的值,a,b的准确值为 ( )
为藏宝处E,三个藏宝处在以B为焦点,椰子树的南北方向所在直线为相应的准线的双曲线上.寻宝的关键是推出a,b的值,a,b的准确值为 ( )
A.28;4 B.14;4 C.28;8 D.14; 8
11.锐角三角形ABC中,若![]() ,则下列叙述正确的是
( )
,则下列叙述正确的是
( )
①![]() ②
②![]() ③
③![]() ④
④![]()
A.①② B.②③ C.③④ D.④①
12.(理)过正方体任意两个顶点的直线共28条,其中异面直线有
A.32对 B.72对 C.174对 D.189对
(文)若O是平面上的定点,A、B、C是平面上不共线的三点,且满足![]() (
(![]() ),则P点的轨迹一定过△ABC的
),则P点的轨迹一定过△ABC的
A.外心 B.内心 C.重心 D.垂心
二、填空题:本大题共4个小题,每小题4分,共16分. 把答案直接写在横线上
13.某计算机执行以下程序:
(1)初始值x = 3,s = 0;
(2)x = x + 2;
(3)s = s + x;
(4)若s≥2003,则进行(5),否则从(2)继续执行;
(5)打印x;
(6)stop。
那么由语句(5)打印出的数值为__________________.
14.(理)设![]() 的展开式中各项系数之和为A,各项的二项式系数之和为B,如A+B=272,则展开式中
的展开式中各项系数之和为A,各项的二项式系数之和为B,如A+B=272,则展开式中![]() 的系数为
。
的系数为
。
(文)![]() 展开式中
展开式中![]() 的系数是
。
的系数是
。
15.在△ABC中,B(-2,0)、C(2,0)、A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下面给出了一些条件及方程,请你用线把左边△ABC满足的条件及相应的右边A点的轨迹方程连起来.(错一条连线得0分)
① △ABC周长为10 ![]() : y2=25
: y2=25
② △ABC面积为10
![]() : x2+y2=4(y≠0)
: x2+y2=4(y≠0)
③ △ABC中,∠A=90°
![]() :
: ![]() +
+![]() =1(y≠0)
=1(y≠0)
16.现用若干张扑克牌进行扑克牌游戏.小明背对小亮,让小亮按下列四个步骤操作:
第一步:分发左、中、右三堆牌,每堆牌不少于两张,且各堆牌的张数相同;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出一张,放入中间一堆;
第四步:左边一堆有几张牌,就从中间一堆拿出几张牌放入左边一堆.
这时,小明准确地说出了中间一堆牌现有的张数.你认为中间一堆牌的张数是 .
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)已知![]() ,将
,将![]() 的图象按向量
的图象按向量![]() 平移后,图象关于直线
平移后,图象关于直线![]() 对称.
对称.
(1)求实数![]() 的值,并求
的值,并求![]() 取得最大值时
取得最大值时![]() 的集合;
的集合;
(2)求![]() 的单调递增区间.
的单调递增区间.
18.(本小题满分12分)(理)口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为![]() .
.
(1)![]() 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;
(2)求随机变量![]() 的期望
的期望![]() .
.
(文)有一种博彩游戏,其规则如下:庄家在口袋里装黑、白围棋子各8枚,博彩者从中随机一次摸出5枚,摸一次交手续费1元,中彩情况如下:
| 摸子情况 | 5枚白 | 4枚白 | 3枚白 | 其它 |
| 彩 金 | 20元 | 2元 | 纪念品价值5角 | 无奖 |
(1)分别求博彩一次获20元彩金,2元彩金,纪念品的概率;
(2)如果游客博彩1000次,庄家是赔钱还是赚钱?金额约是多少元?(精确到元)
19.(本题满分12分)、如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(1)若k=1,试求异面直线PA与BD所成角余弦值的大小.
 (2)当k取何值时,二面角O-PC-B大小为
(2)当k取何值时,二面角O-PC-B大小为![]() ?
?
20.(本题共12分)已知数列![]() 中,
中,![]() ,且
,且![]() .
.
(1)若![]() ,求证:数列
,求证:数列![]() 是等比数列.
是等比数列.
(2)求数列![]() 的通项公式.
的通项公式.
(3)(仅理科)若![]() ,试比较
,试比较![]() …
…![]() 与
与![]()
![]() .
.
21.(本题满分12分)已知抛物线y2 = 2px ( p>0)的焦点为F,直线l过定点A(1,0)且与抛物线交于P、Q两点.
(1)若以弦PQ为直径的圆恒过原点O,求P的值;
(2)在(1)的条件下,若 ![]() +
+ ![]() =
= ![]() ,求动点R的轨迹方程.
,求动点R的轨迹方程.
22.(本小题满分14分)已知数列{![]() }中,
}中,![]() (n≥2,
(n≥2,![]() ),
),
(1)若![]() ,数列
,数列![]() 满足
满足![]() (
(![]() ),求证数列{
),求证数列{![]() }是等差数列;
}是等差数列;
(2)若![]() ,求数列{
,求数列{![]() }中的最大项与最小项,并说明理由;
}中的最大项与最小项,并说明理由;
(3)(理做文不做)若![]() ,试证明:
,试证明:![]() .
.
参考答案
1.(理)D ![]() 。
。
点评:据“纯虚数”概念,求出a,再对![]() 化简求值。其思想是分母实数化——分子分母同乘以
化简求值。其思想是分母实数化——分子分母同乘以![]() 的共轭复数
的共轭复数![]() ,这种思想与分母(分子)实数化的思想是一致的。此题的另一个技巧处理是:
,这种思想与分母(分子)实数化的思想是一致的。此题的另一个技巧处理是:![]()
(文)C ![]() 恒成立,所以
恒成立,所以![]() 为
为![]() 的增函数。
的增函数。
点评:对三次函数常见的处理方式是先求导降次,再由![]() 判断二次式根的情况。
判断二次式根的情况。
2.A.集合![]() 是有序实数对,是二维的,而集合
是有序实数对,是二维的,而集合![]() 是函数的值域,是一维的,因此
是函数的值域,是一维的,因此![]() ,故选A.
,故选A.
点评:本题关键是正确理解集合M、N各自的意义,否则,容易误以为是直线与抛物线的交点.
3.A
⊙O′的半径为1,球O的半径为![]() ,所以OO′的长度为
,所以OO′的长度为![]()
点析:“球面距”是球中很重要的一个概念。此题最终目的是对球中一个重要直角三角形(小圆半径、球半径、球心到小圆面的距离构成的一个直角三角形)的考查,这也是高考的常考点。
4.C. 通过读图形,显然可以得到![]() ,
,![]() ,将原点坐标代入
,将原点坐标代入![]() 知成立.
知成立.
点析:线性规划是高中的新增的知识点,一般在选择、填空题中出现.
5.C A错,当直线m、n都平行于平面α时,这两条直线平行、相交、异面皆有可能。B错,因为没有点明直线的位置。C正确。D错,此时的直线n可能与平面α相交,也可能在α内。故选C。
点析:本题主要考查了立体几何的关系的判断,是一道多选题。此类题的思维容量大,考查的知识覆盖面广,也是高考考查的一类热点问题。
6.(理)A 由已知椭圆与双曲线有相同的焦点可知a2
–b2 = m2 +n2,又c2 = am,2n2
= 2m2 +c2, 解得a2 = 16m2,b2=12m2,∴椭圆的离心率为e=![]() 。选A。
。选A。
点析:本题以椭圆与双曲线共焦点为背景,将等差中项、等比中项的基本运算融合进来,对计算及解方程的能力要求较高,这也正体现了2007年最新的《考试大纲》中对运算能力的考查要求。
(文)A 不妨设双曲线的方程为![]() (a>0,b>0),则渐近线的方程为
(a>0,b>0),则渐近线的方程为![]() ,准线方程为x =±
,准线方程为x =±![]() 。设双曲线的准线x =
。设双曲线的准线x =![]() 与其渐近线
与其渐近线![]() 分别相交于A、B 两点,由双曲线的性可知 A、B两点关于x轴对称,易求得CF=c -
分别相交于A、B 两点,由双曲线的性可知 A、B两点关于x轴对称,易求得CF=c - ![]() =
=![]() ,又AB=2CA=2×
,又AB=2CA=2×![]() ×
×![]() =
=![]() ,又∵△ABF为等边三角形,∴CF=
,又∵△ABF为等边三角形,∴CF=![]() AB, 即
AB, 即![]() =
=![]() ×
×![]() ,整理得
,整理得![]() ab=b2,∴
ab=b2,∴![]() ,从而e =
,从而e = ![]() 。故选A.
。故选A.
点析:此题虽然是关于双曲线的一个基本计算题,但它不仅考查了双曲线的基本概念及基本性质,还将离心率的计算与等边三角形中的线段的计算相结合,使得题目的内涵增大,考查功能增强,解决此类题目要求考生有较强的运算能力和较强的分析问题、解决问题的能力。
7.A 曲线y=2sin(x + )cos(x - )=2 sin( - x ) cos(-x)= sin(2 -2x)=2COS2x,由此做出函数图象,再分析P1,P2,P3,…的具体位置,求出P2P4=π
点析:本题主要体现了三角函数的二倍角公式,以及余弦函数的图象特征,由此解决问题,解决问题时时画出图象,帮助分析更加直观。
8.(理)D.由![]() 是R上的奇函数可知,
是R上的奇函数可知,![]() ,即x=0是原不等式的解,则正确答案是C、D中之一;∵
,即x=0是原不等式的解,则正确答案是C、D中之一;∵![]() 或
或![]() ,又当x<0时,
,又当x<0时,![]() ,且
,且![]() ,可以推出
,可以推出![]() 是R+上为增函数,∴
是R+上为增函数,∴![]() 时,
时,![]() ,
,![]() 是原不等式的解.故选D.
是原不等式的解.故选D.
点析:首先要根据题意掌握函数![]() 的特性(最好画出其草图),其次利用特殊值法或解不等式组都能解决这类问题.
的特性(最好画出其草图),其次利用特殊值法或解不等式组都能解决这类问题.
(文)A.在![]() 中取
中取![]() ,
,
则![]() 即函数
即函数![]() 是周期为6的函数,∴
是周期为6的函数,∴![]() ,
,![]() ,所以
,所以![]() .
.
点析:大多数这类求![]() 等等值的问题都是转化为周期函数来解.因此取
等等值的问题都是转化为周期函数来解.因此取![]() 得到
得到![]() 和
和![]() 是周期为6的函数.
是周期为6的函数.
9.C
![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() 。
。
点析:此题本质是考查函数![]() 及其复合函数的单调性。如果按常规思路,先求出
及其复合函数的单调性。如果按常规思路,先求出![]() ,再求出
,再求出![]() 的取值范围,势必比较麻烦。
的取值范围,势必比较麻烦。
10.建立坐标系,由第二定义得, 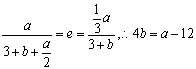 ,然后特值验证,选A;
,然后特值验证,选A;
点析:利用圆锥曲线的几何量解决应用问题,这本身就是学习数学的出发点和归宿. 对于选择题常常选择支验证,如本题由第二定义得到二元一次方程时应验证选择支求解.
11.B
![]()
![]()
![]()
![]() 。
。
点析:三角形中的三角函数有关问题是历来考查的一个重点。此题中对于![]() 同学们会误认为
同学们会误认为![]() ,而认为
,而认为![]() 是错误的。殊不知
是错误的。殊不知![]() ,此外对
,此外对![]() 的处理(利用正弦定理,将其转化成角的关系)也是需要积累的。
的处理(利用正弦定理,将其转化成角的关系)也是需要积累的。
12.(理)C 法一:1 正方体八个顶点共面有12种情况,且每个面内涉及![]() 条直线。2 以正方体的8个顶点为顶点的等边三角形共有8个,且每个等边三角形涉及3条直线。故所有异面直线的对数为
条直线。2 以正方体的8个顶点为顶点的等边三角形共有8个,且每个等边三角形涉及3条直线。故所有异面直线的对数为![]() 。
。
法二:以正方体的8个顶点为顶点的三棱锥有![]() 个,任意一个三棱锥中有3对异面直线的对数为
个,任意一个三棱锥中有3对异面直线的对数为![]() 。所以正确答案为C。
。所以正确答案为C。
点析:此题沿袭2005全国Ⅰ(理)12题,考查的难度比较大,需要认真仔细分析找到解题路径。最后多总结,把本题的解法总结成一种思路。
(文)C ![]() (D为AB边的中点)。
(D为AB边的中点)。
点析:对三角形中的“中线向量公式”应该引起重视。学生可进一步思考其他几“心”,如:满足![]() 的P点的轨迹一定过△ABC的垂心。
的P点的轨迹一定过△ABC的垂心。
13.89 由题意可知,数列{an}是以5为首项,2为公差的等差数列,Sn是等差数列{xn}的前n项和。由Sn = 5n + ![]() ≥2003,可解得n≥43. ∴ x43=5+(43-1)×2=89.∴由语句(5)打印出的数值为89.
≥2003,可解得n≥43. ∴ x43=5+(43-1)×2=89.∴由语句(5)打印出的数值为89.
点析:本题以计算机程序语言为背景考查等差数列的通项公式与前n项和公式,迁移与转化能力是解决这一类问题的关键。
14.(理) 赋值法得A=![]() ,B=
,B=![]() ,所以
,所以![]() ,所以含
,所以含![]() 项为
项为![]() ,所以正确答案应该填108。
,所以正确答案应该填108。
(文) 因为![]() ,所以正确答案应该填-160
,所以正确答案应该填-160
点析:项的系数与二项式的系数是不同的两个概念,而求各项的系数和应采用赋值法,求二项式系数和利用公式![]() 。
。
15.①→![]() , ②→
, ②→![]() , ③→
, ③→![]() .① 由AB+AC=6,得
.① 由AB+AC=6,得![]() +
+![]() =1(y≠0);
=1(y≠0);
② 由![]() BCy=10,得y2=25;③ 由AB2+AC2=BC2,得x2+y2=4(y≠0).
BCy=10,得y2=25;③ 由AB2+AC2=BC2,得x2+y2=4(y≠0).
点析:本题的设计是比较新颖的,是一道配对型的选择性的填空题.显然是一道活题,是考知识、考能力的好题.
16. 5. 按各放2张,你可以算出正确的答案是5.各放![]() 张呢,答案应当是一样的呀!
张呢,答案应当是一样的呀!
点析:考试大纲中要求,考查学生的实践能力,动手操作能力.本题将数学与日常的游戏结合起来,显示了淡化知识,重视能力的命题新格局.
17.(1)![]() ,将
,将![]() 的图象按向量
的图象按向量![]() 平移后的解析式为
平移后的解析式为![]()
![]() .…………………………3分
.…………………………3分
![]() 的图象关于直线
的图象关于直线![]() 对称,
对称,
![]() 有
有![]() ,即
,即![]() ,解得
,解得![]() . ……………………5分
. ……………………5分
则![]() . ……………………………6分
. ……………………………6分
当![]() ,即
,即![]() 时,
时,![]() 取得最大值2.…………………7分
取得最大值2.…………………7分
因此,![]() 取得最大值时
取得最大值时![]() 的集合是
的集合是![]() .……………………8分
.……………………8分
(2)由![]() ,解得
,解得![]() .
.
因此,![]() 的单调递增区间是
的单调递增区间是![]()
![]() .……………………12分
.……………………12分
点析:本题是一个常规性考查三角函数的题目,第一问要先化简解析式,然后利用向量的平移公式求出平移后的函数解析式,再利用对称性确定出a的值后,用整体法求单调区间。
18. (理)(1)依题意,随机变量![]() 的取值是2、3、4、5、6. (2分)
的取值是2、3、4、5、6. (2分)
因为P(![]() =2)=
=2)=![]() ;P(
;P(![]() =3)=
=3)=![]() ,
,
P(![]() =4)=
=4)=![]() ;P(
;P(![]() =5)=
=5)=![]() ;
;
P(![]() =6)=
=6)=![]() ; (7分)
; (7分)
所以,当![]() =4时,其发生的概率P(
=4时,其发生的概率P(![]() =4)=
=4)=![]() 最大. (6分)
最大. (6分)
(2)E![]() =
=![]() . (12分)
. (12分)
点析:概率解答试题理科多是高三的概率与统计内容,而文科则多出现在高二的概率知识里.这点应当引起我们在复课时的注意.
(文)(1)一次摸奖中20元彩金的概率![]() ; (2分)
; (2分)
一次摸奖中2元彩金的概率![]() ;
;
中纪念奖概率 ![]() (6分)
(6分)
(2)1000次收手续费1000元.
预计支付20元奖需![]() ;
;
支付2元奖需![]() 元; (9分)
元; (9分)
支付纪念奖需![]() 元;
元;
则余额n=1000-m20-m2-m纪=308元.
故庄家赚钱约308元. (12分)
点析:概率知识的复习应当紧扣课本,紧扣高考真题.在课本上的基本概念、基础知识的熟练掌握和深刻理解的前提下,适度提升复习的门槛,这也许是有效学习,高效速练的好办法.
19.法一:(1)设AB=a,由点O、D分别是AC、PC的中点知:![]() 为所求异面直线PA与BD所成角.
为所求异面直线PA与BD所成角.![]()
又OP⊥底面ABC,
![]()
![]() .从而
.从而
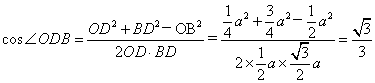 .
.
即异面直线PA与BD所成角余弦值的大小为![]() .
.
(2)过O作OE![]() PC交PC于E,
PC交PC于E,
![]()
![]() 有、
有、![]() 为所求二面角O-PC-B的平面角.设AB=a,PO=h.
为所求二面角O-PC-B的平面角.设AB=a,PO=h.
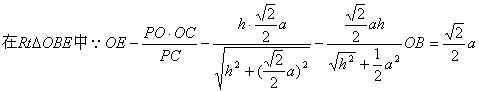
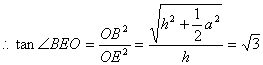 ,解得
,解得![]()
.![]()

故当 k=![]() 时,二面角O-PC-B大小为
时,二面角O-PC-B大小为 ![]()
法二:(向量法)
易证OP⊥平面ABC,又OA=OC,AB=BC,
从而OA⊥OB,OA⊥OB,OB⊥OP
以O为原点,射线OP为非负x轴,
建立空间直角坐标系O-xyz ,(1)设AB=a,则![]() ,
,![]() ,
,
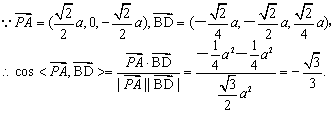
即异面直线PA与BD所成角余弦值的大小为![]() .
.
(3)设AB=a,![]()
![]() 为平面OPC的一个法向量.
为平面OPC的一个法向量.
不妨设平面PBC的一个法向量为![]() ,
,![]()
![]()
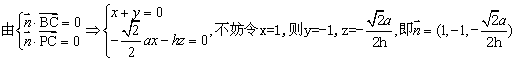
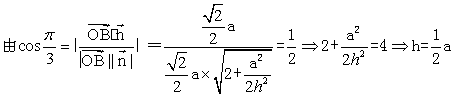
![]()
故当 k=![]() 时,二面角O-PC-B大小为
时,二面角O-PC-B大小为![]() .
.
点析:设计“一题二法”是近几年立体几何综合的基本模式。考查一题多解。其实是在考查考生的解三角形知识,考试结果表明,一般学生解题中遇到的主要障碍也在于此。本题给我们的教学启示是——要关注立体几何命题与三角函数、解三角形知识之间的联系,在教学实践中要指导学生如何运用分析的方法,从复杂的空间图形关系中抽象出对应的三角形,掌握“化空间问题为平面问题,化复杂问题为简单问题”的化归思想,同时注意掌握求解折叠问题的解法规律.另外,通过本题要教会学生如何在一般图形中,建立恰当的空间直角坐标系.
20.⑴由已知得![]() ,∴
,∴![]() ,∴
,∴![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列……………………………………3分(文5分)
的等比数列……………………………………3分(文5分)
⑵由⑴得![]() ,即
,即![]() ,………4分(文7分)
,………4分(文7分)
∴![]() ,
,![]() ,…,
,…,![]() ,
,
将上列各等式相加得![]() ,∴
,∴![]() …………..6分(文9分)
…………..6分(文9分)
又![]() 时,
时,![]() …
…![]() ,∴
,∴![]()
综上可知![]() …………………………………………………8分(文科12分)
…………………………………………………8分(文科12分)
⑶由![]() 得
得![]() …………………………9分
…………………………9分
∵![]() ,又
,又![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() …………………………10分
…………………………10分
∴![]() …
…![]() …
…![]() …
…![]()
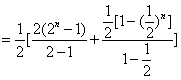
![]()
![]() 12分
12分
点析:含有数列递推公式的问题,一般是对递推公式进行变形,将其转化为等差数列或等比数列,再求出通项.如本题(1);另外在解决问题的过程中,要注意特殊情形的讨论(如n=1,q=1,d=0等等),如本题(2);对大小比较的问题,应先根据题意判断大小,再证明你的结论.如本题(3),在“![]() …
…![]() ”和“
”和“![]()
![]() ”的启发下,容易联想到将
”的启发下,容易联想到将![]() 放缩成两个等比数列(公比应该为2和
放缩成两个等比数列(公比应该为2和![]() ),最后发现
),最后发现![]() .这类问题在近几年的高考试题中经常出现.
.这类问题在近几年的高考试题中经常出现.
21.(1)①若直线为x = 1,将x = 1代入y2 = 2px得y2 = 2p
以弦PQ为直径的圆恒过原点 O ,所以有2p = 1∴ P = 1/2
②若直线l不是 x = 1时,设直线方程为: y = kx – k
将y = kx – k 代入y2 = 2px得 k2 x2 - (2p + 2k2)x + k2 = 0①
设P(x1,y1) Q(x2,y2)则由韦达定理得:
x1 + x2 = (2p + 2k2)/ k2
x1 x2 =1 故 y1y2 = - 2p 又以弦PQ为直径的圆恒过原点O,
∴ x1 x2+ y1y2 =0= 1- 2p ∴ P = 1/2
又 此时D = 4p2 + 8pk2 > 0综合①②得 P = 1/2. ………………6分
(2)设动点R的坐标为(x,y)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∵ FP + FQ = FR ∴FO + OP + FO + OQ = FO + OR
∵ FP + FQ = FR ∴FO + OP + FO + OQ = FO + OR
∴ (-1/4,0) + (x1,y1) + (x2,y2)= (x,y)
∴ x= x1 + x2 - 1/4且 y =y1 +y2
①l 方程为 x= 1时,x= x1 + x2 - 1/4= 7/4 ,y =y1 +y2= 0
②当 l 方程不是 x= 1时,x=(2p +2k2)/k2 – 1/4
y= k(x1 + x2) - 2k = 1/k
即得 :x= 2p y2 + 7/4 = y2 + 7/4 所以 y2 = x –7/4
又因为 点(7/4,0)在y2 = x –7/4 上
∴ 由①②得R点的轨迹方程为:y2 = x –7/4 ………………12分
点析:本题是一个解析几何与平面向量结合的题目,是近几年高考的一个热点题型,再就是本题主要体现了分类讨论的思想方法,在两个问法里面都分两种情况。实际主要根据了直线的斜率是否存在来进行,也是涉及直线问题的一个易错环节。
22.(1)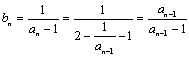 ,而
,而 ![]() ,
,
∴ ![]() .
.![]()
∴ {![]() }是首项为
}是首项为![]() ,公差为1的等差数列. (4分)
,公差为1的等差数列. (4分)
(2)
有![]() ,而
,而![]() , ∴
, ∴ ![]() .对于函数
.对于函数![]() ,在x>3.5时,y>0,
,在x>3.5时,y>0,![]() ,在(3.5,
,在(3.5,![]() )上为减函数. 故当n=4时,
)上为减函数. 故当n=4时,![]() 取最大值3.(6分)而函数
取最大值3.(6分)而函数![]() 在x<3.5时,y<0,
在x<3.5时,y<0,![]() ,在(
,在(![]() ,3.5)上也为减函数.故当n=3时,取最小值,
,3.5)上也为减函数.故当n=3时,取最小值,![]() =-1.(8分
=-1.(8分
(3)
用数学归纳法证明![]() ,再证明
,再证明![]()
. ① 当![]() 时,
时,![]() 成立; (9分)
成立; (9分)
②假设当![]() 时命题成立,即
时命题成立,即![]() ,
,
当![]() 时,
时,![]()
![]()
![]()
![]()
故当![]() 时也成立, (11分)
时也成立, (11分)
综合①②有,命题对任意![]() 时成立,即
时成立,即![]() . (12分)
. (12分)
(也可设![]() (1≤
(1≤![]() ≤2),则
≤2),则![]() ,
,
故![]()
![]()
![]() ).
).
下证:![]()
![]()
![]()
![]() .(14分)
.(14分)
点析:本题对等差数列的证明,数列项的最值的方法(函数单调性的定义法和导数法)以及数学归纳法证明不等式进行了全面的考查.
欢迎访问 http://www.k12zy.com