2006-2007学年度上学期
高中学生学科素质训练
高三数学第一轮复习单元测试(10)—《极限、导数》
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一
个选项正确
1.(理)若复数![]() 满足方程
满足方程![]() ,则
,则![]() ( )
( )
A.![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
(文)曲线y=4x-x3在点(-1,-3)处的切线方程是 ( )
A. y=7x+4 B. y=7x+2 C. y=x-4 D. y=x-2
2.函数y=x2(-![]() ≤x≤
≤x≤![]() )图象上一点P,以点P为切点的切线为直线l,则直线l的倾斜角
)图象上一点P,以点P为切点的切线为直线l,则直线l的倾斜角
的范围是 ( )
A.[0,![]() ]∪[
]∪[![]() ,π] B.[0,π]
,π] B.[0,π]
C.[![]() ,
,![]() ] D.[0,
] D.[0,![]() ]∪(
]∪(![]() ,
,![]() )
)
3.(理)若![]()
![]() ,则a的值为 ( )
,则a的值为 ( )
A.0
B.1 C.-1 D. ![]()
(文)在曲线y=x2+1的图象上取一点(1,2)及邻近一点(1+Δx,2+Δy),则![]() 为( )
为( )
A.Δx+![]() +2 B.Δx-
+2 B.Δx-![]() -2
-2
C.Δx+2 D.2+Δx-![]()
4.曲线y=![]() x5+3x2+4x在x=-1处的切线的倾斜角是 ( )
x5+3x2+4x在x=-1处的切线的倾斜角是 ( )
A.-![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.函数f(x)=x3-ax2-bx+a2在x=1时,有极值10,则a、b的值为 ( )
A.![]() B.
B.![]()
C.![]() D.以上皆错
D.以上皆错
6.(理)已知![]() ,下面结论正确的是 ( )
,下面结论正确的是 ( )
A.![]() 在
在![]() 处连续
B.
处连续
B.![]()
C.![]() D.
D.![]()
(文)设f(x)=ax3+3x2+2,若f′(-1)=4,则a的值等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数f(x)=x3-3x+1,x∈[-3,0]的最大值、最小值分别是 ( )
A.1,-1 B.1,-17 C.3, -17 D.9,-19
8.(理)数列{an}中,a1=1,Sn
是前n项和.当n≥2时,an=3Sn,则![]()
![]() 的值是( )
的值是( )
A.-![]() B.-2 C.1
D.-
B.-2 C.1
D.-![]()
(文)曲线y=x3-3x2+1在点(1,-1)处的切线方程为 ( )
A.y=3x-4 B.y=-3x+2 C.y=-4x+3 D.y=4x-5
9.(理)2+2![]() i的平方根是 ( )
i的平方根是 ( )
A.![]() +i
B.
+i
B.![]() ±i C.±
±i C.±![]() +i D.±(
+i D.±(![]() +i)
+i)
(文)已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值是 ( )
A.-37 B.-29 C.-5 D.以上都不对
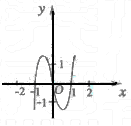 10.已知函数
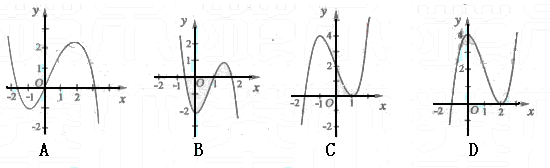
10.已知函数![]() 的图象如右图所示(其中
的图象如右图所示(其中 ![]() 是函数
是函数![]() 的导函数),下面四个图象中
的导函数),下面四个图象中![]() 的图象大致是
的图象大致是
11.设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,![]() >0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
>0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0, 3)
C.(-∞,- 3)∪(3,+∞) D.(-∞,- 3)∪(0, 3)
12.已知两点O(0,0),Q(![]() ,b),点P1是线段OQ的中点,点P2是线段QP1的中点,P3是线段P1P2的中点,┅,
,b),点P1是线段OQ的中点,点P2是线段QP1的中点,P3是线段P1P2的中点,┅,![]() 是线段
是线段![]()
![]() 的中点,则点
的中点,则点![]() 的极限位置应是( )
的极限位置应是( )
A.(![]() ,
,![]() )
B.(
)
B.(![]() ) C.(
) C.(![]() ) D. (
) D. (![]() )
)
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
13.垂直于直线2x-6y+1=0且与曲线y=x3+3x2-1相切的直线方程的一般式是__________.
14.(理) (2006年安徽卷)设常数![]() ,
,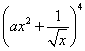 展开式中
展开式中![]() 的系数为
的系数为![]() ,则
,则![]() _____.
_____.
(文)(2006福建高考)已知直线![]() 与抛物线
与抛物线![]() 相切,则
相切,则![]()
15.函数f(x)=2x3+3x2-12x-5,则函数f(x)的单调增区间是______.
16.(理)用数学归纳法证![]()
的过程中,当n=k到n=k+1时,左边所增加的项为_______________.
(文)若函数f(x)=x3+x2+mx+1是R上的单调递增函数,则m的取值范围是______________.
三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分12分)
(理)设函数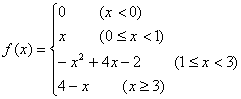
(1)画出函数的图象;
(2)在x=0,x=3处函数![]() 是否连续;
是否连续;
(3)求函数![]() 的连续区间.
的连续区间.
(文)已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若曲线![]() 上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
18.(本题满分12分)
(理)已知复数z1=cosθ-i,z2=sinθ+i,求 z1·z2的最大值和最小值.
(文)(2006福建高考)已知![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集是
的解集是![]() 且
且![]() 在区间
在区间![]() 上的最大值是12。
上的最大值是12。
(1)求![]() 的解析式;
的解析式;
(2)是否存在实数![]() 使得方程
使得方程![]() 在区间
在区间![]() 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
19.(本小题满分12分)
已知![]() 有极大值
有极大值![]() 和极小值
和极小值![]() .
.
(1)求![]() +
+![]() 的值;
的值;
(2)设曲线![]() 的极值点为A、B,求证:线段AB的中点在
的极值点为A、B,求证:线段AB的中点在![]() 上.
上.
20.(本小题满分12分)
(理)函数![]() 的定义域为R,且
的定义域为R,且![]()
(1)求证:![]()
(2)若![]() 上的最小值为
上的最小值为![]() ,
,
求证:![]()
![]() .
.
(文)(2006安徽高考)设函数![]() ,已知
,已知![]() 是奇函数。
是奇函数。
(1)求![]() 、
、![]() 的值.
的值.
(2)求![]() 的单调区间与极值.
的单调区间与极值.
21.(本小题满分12分)
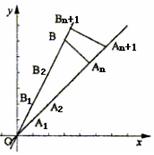 (理)如图,在平面直角坐标系xOy中,射线
(理)如图,在平面直角坐标系xOy中,射线![]() 上依次有点列A1,A2…,An,…;B1,B2,…,Bn,….其
上依次有点列A1,A2…,An,…;B1,B2,…,Bn,….其
中![]() ,
,
![]()
(1)用含有n的式子表示![]() ;
;
(2)用含有n的式子表示点An、Bn的坐标;
(3)求四边形![]() 面积的最大值.
面积的最大值.
(文)(2006陕西高考)已知函数f(x)=kx3-3x2+1(k≥0).
(1)求函数f(x)的单调区间;
(2)若函数f(x)的极小值大于0, 求k的取值范围.
22.(本大题满分14分)
自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量,n∈N*,且x1>0.不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,这些比例系数依次为正常数a,b,c.
(1)求xn+1与xn的关系式;
(2)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
(3)(只理科做)设a=2,b=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的最大允许值是多少?证明你的结论.
参考答案(10)
1.(理)设![]() ,由
,由![]() ,得
,得![]() ,得
,得![]() 。所以
。所以![]() .答案:D
.答案:D
(文)![]() ,所以k切=4-3×(-1)2=1,运用直线的点斜式方程得y=4x-x3在点(-1,-3)处的切线方程是y=x-2,所以应选D.
,所以k切=4-3×(-1)2=1,运用直线的点斜式方程得y=4x-x3在点(-1,-3)处的切线方程是y=x-2,所以应选D.
2.y′=2x.∵-![]() ≤x≤
≤x≤![]() ,∴-1≤y′≤1,即-1≤tanα≤1.又∵0≤α<π,∴0≤α≤
,∴-1≤y′≤1,即-1≤tanα≤1.又∵0≤α<π,∴0≤α≤![]() 或
或![]() ≤α<π.答案:A
≤α<π.答案:A
3.(理)∵![]()
![]() 存在,而把x=2代入分母时,分母为零,∴分子、分母应有(x-2)这一公因式,化简以后,再求极限.∴分子x2+ax-2可分解成(x-2)(x+1),即x2+ax-2=(x-2)(x+1)=x2-x-2.∴a=-1.答案: C
存在,而把x=2代入分母时,分母为零,∴分子、分母应有(x-2)这一公因式,化简以后,再求极限.∴分子x2+ax-2可分解成(x-2)(x+1),即x2+ax-2=(x-2)(x+1)=x2-x-2.∴a=-1.答案: C
(文)![]() =
=![]() =Δx+2.答案:C
=Δx+2.答案:C
4.y′=x4+6x+4,∴y′![]() =(-1)4+6(-1)+4=-1.由tanα=-1,0≤α<π,得α=
=(-1)4+6(-1)+4=-1.由tanα=-1,0≤α<π,得α=![]() π.
π.
答案:C
5.f′(x)=3x2-2ax-b.∵函数f(x)在x=1处有极值10,∴![]() 解得
解得![]() 答案:A
答案:A
6.(理) 当x=1 时,2x+3=5![]() 2,故A、B错误;而
2,故A、B错误;而![]() =5,故选D.
=5,故选D.
(文)f′(x)=3ax2+6x,f′(-1)=3a-6=4,所以a=![]() .答案:D
.答案:D
7.f′(x)=3x2-3=3(x-1)(x+1).令f′(x)=0得x=-1或x=1(舍去).
列表如下:
| x | -3 | (-3, -1) | -1 | (-1,0) | 0 |
| f(x) | -17 | ↗ | 3 | ↘ | 1 |
∴f(x)max=3,f(x)min=-17.答案:C
8.(理)当n≥2时,an=Sn-Sn-1=3Sn,∴Sn=-![]() Sn-1.又S1=a1=1,∴{Sn}是以1为首项,-
Sn-1.又S1=a1=1,∴{Sn}是以1为首项,-![]() 为公比的等比数列.∴
为公比的等比数列.∴![]()
![]() =
= ![]()
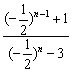 =-
=-![]() .答案: A
.答案: A
(文)y′=3x2-6x,∴y′x=1=-3.∴在(1,-1)处的切线方程为y+1=-3(x-1).答案:B
9.(理)设2+2![]() i的平方根是a+bi(a、b∈R),
i的平方根是a+bi(a、b∈R),
则(a+bi)2=2+2![]() i,即a2-b2+2abi=2+2
i,即a2-b2+2abi=2+2![]() i.由复数相等的定义,得
i.由复数相等的定义,得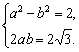
解得![]() 或
或![]() 即2+2
即2+2![]() i的平方根是±(
i的平方根是±(![]() +i).答案:D
+i).答案:D
(文)![]() (x)=6x(x-2),f(x)在(-2,0)上为增函数,在(0,2)上为减函数的,x=0时,f(x)=m最大.∴m=3,f(-2)=-37,f(2)=-5.答案:A
(x)=6x(x-2),f(x)在(-2,0)上为增函数,在(0,2)上为减函数的,x=0时,f(x)=m最大.∴m=3,f(-2)=-37,f(2)=-5.答案:A
10.由函数![]() 的图象可知:当
的图象可知:当![]() 时,
时, ![]() <0,
<0,![]() >0,此时
>0,此时![]() 增,当
增,当![]() 时,
时,![]() >0,
>0,![]() <0,此时
<0,此时![]() 减,当
减,当![]() 时,
时,![]() <0,
<0,![]() <0,此时
<0,此时![]() 减,当
减,当![]() 时,
时,![]() >0,
>0,![]() >0,此时
>0,此时![]() 增.答案:C
增.答案:C
11.∵当x<0时,![]() >0 ,即
>0 ,即![]() ,∴当x<0时,f(x)g(x)为增函数,又g(x)是偶函数且g(3)=0,∴g(-3)=0,∴f(-3)g(-3)=0,故当
,∴当x<0时,f(x)g(x)为增函数,又g(x)是偶函数且g(3)=0,∴g(-3)=0,∴f(-3)g(-3)=0,故当![]() 时,f(x)g(x)<0,又f(x)g(x)是奇函数,当x>0时,f(x)g(x)为减函数,且f(3)g(3)=0,故当
时,f(x)g(x)<0,又f(x)g(x)是奇函数,当x>0时,f(x)g(x)为减函数,且f(3)g(3)=0,故当![]() 时,f(x)g(x)<0,故选D
时,f(x)g(x)<0,故选D
12.∵点![]() 的位置应是(
的位置应是(![]() ,∴点
,∴点![]() 的极限位置应是(
的极限位置应是(![]() ).答案:C
).答案:C
13.∵所求直线与2x-6y+1=0垂直,∴k=-3.又由y=x3+3x2-1,得y′=3x2+6x=-3.∴x=-1,切点为(-1,1).∴直线方程为y-1=-3(x+1),即3x+y+2=0.答案: 3x+y+2=0
14.(理) ![]() ,由
,由![]()
![]() ,所以
,所以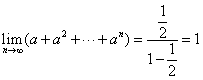 ,所以为1.
,所以为1.
(文)∵ 直线![]() 与抛物线
与抛物线![]() 相切,切线的斜率
相切,切线的斜率![]() ,∴切点
,∴切点![]() ,而切点又在抛物线
,而切点又在抛物线![]() 上,∴
上,∴ ![]() 故
故![]() .
.
15.分析:本题考查用导数求函数的单调区间,但要注意单调区间的写法.解:f′(x)=6x2+6x-12,令f′(x)>0,得6x2+6x-12>0,解得x<-2或x>1,即函数f(x)的单调增区间是(-∞,-2)或(1,+∞).答案:(-∞,-2)或(1,+∞)
16.(理)当n=k到n=k+1时,左边增加了两项![]() ,减少了一项
,减少了一项![]() ,左边所增加的项为
,左边所增加的项为![]() -
-![]() =
=![]() .答案:
.答案:![]()
(文)f′(x)=3x2+2x+m.∵f(x)在R上是单调递增函数,∴f′(x)>0在R上恒成立,即3x2+2x+m>0.由Δ=4-4×3m<0,得m>![]() .答案:m>
.答案:m>![]()
17.(理)⑴图略;
⑵![]() ,
,
![]() ,
,![]() 处连续 , 同理
处连续 , 同理![]() 处连续;
处连续;
⑶连续区间为(-∞,+∞).
(文)(1)由题设知![]() .
.
令![]() .
.
当(i)a>0时,
若![]() ,则
,则![]() ,所以
,所以![]() 在区间
在区间![]() 上是增函数;
上是增函数;
若![]() ,则
,则![]() ,所以
,所以![]() 在区间
在区间![]() 上是减函数;
上是减函数;
若![]() ,则
,则![]() ,所以
,所以![]() 在区间
在区间![]() 上是增函数;
上是增函数;
(i i)当a<0时,
若![]() ,则
,则![]() ,所以
,所以![]() 在区间
在区间![]() 上是减函数;
上是减函数;
若![]() ,则
,则![]() ,所以
,所以![]() 在区间
在区间![]() 上是减函数;
上是减函数;
若![]() ,则
,则![]() ,所以
,所以![]() 在区间
在区间![]() 上是增函数;
上是增函数;
若![]() ,则
,则![]() ,所以
,所以![]() 在区间
在区间![]() 上是减函数.
上是减函数.
(2)由(Ⅰ)的讨论及题设知,曲线![]() 上的两点A、B的纵坐标为函数的极值,且函数
上的两点A、B的纵坐标为函数的极值,且函数![]() 在
在![]() 处分别是取得极值
处分别是取得极值![]() ,
,![]() .
.
因为线段AB与x轴有公共点,所以![]() .
.
即![]() .所以
.所以![]() .
.
故![]() .
.
解得 -1≤a<0或3≤a≤4.
即所求实数a的取值范围是[-1,0]∪[3,4].
18.(理)
|
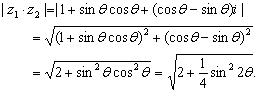
故![]() 的最大值为
的最大值为![]() 最小值为
最小值为![]() .
.
(文)(1)![]()
![]() 是二次函数,且
是二次函数,且![]() 的解集是
的解集是![]()
![]() 可设
可设![]()
![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]()
由已知,得![]()
![]()
(2)方程![]() 等价于方程
等价于方程![]()
设![]() 则
则![]()
当![]() 时,
时,![]() 是减函数;
是减函数;
当![]() 时,
时,![]() 是增函数。
是增函数。
![]()
![]() 方程
方程![]() 在区间
在区间![]() 内分别有惟一实数根,而在区间
内分别有惟一实数根,而在区间![]()
![]() 内没有实数根,
内没有实数根,
所以存在惟一的自然数![]() 使得方程
使得方程![]() 在区间
在区间![]() 内有且只有两个不同的实数根.
内有且只有两个不同的实数根.
19.(1)![]() ,由于
,由于![]() 有极大值和极小值,
有极大值和极小值,
![]() 、
、![]() 的两根,
的两根,
则![]()
![]()
![]()
(2)设![]()
![]()
知AB的中点在![]() 上
上
20.(理)解:⑴![]() 定义域为R,
定义域为R,![]()
![]()
![]()
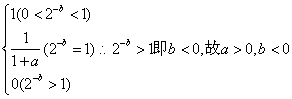
⑵由⑴知![]()
![]()
![]()
![]()
![]()
![]()
(文)(1)∵![]() ,∴
,∴![]() .从而
.从而![]() =
=![]()
是一个奇函数,所以![]() 得
得![]() ,由奇函数定义得
,由奇函数定义得![]() ;
;
(2)由(Ⅰ)知![]() ,从而
,从而![]() ,由此可知,
,由此可知,
![]() 和
和![]() 是函数
是函数![]() 是单调递增区间;
是单调递增区间;
![]() 是函数
是函数![]() 是单调递减区间;
是单调递减区间;
![]() 在
在![]() 时,取得极大值,极大值为
时,取得极大值,极大值为![]() ,
,![]() 在
在![]() 时,取得极小值,极小值为
时,取得极小值,极小值为![]() .
.
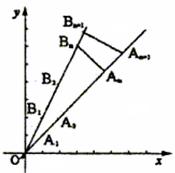
21.(理)⑴由已知得![]() ,
,
![]()
所以,![]() 是首项为
是首项为![]() ,
,
公比为![]() 的等比数列,
的等比数列,
![]()
⑵设![]()
![]() 是首项为
是首项为![]() 公差为
公差为![]() 的等差数列,
的等差数列,
![]()
![]()
![]()
![]()
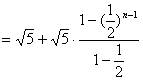
![]()
设![]() . 所以
. 所以![]()
⑶设四边形![]() 的面积是
的面积是![]() ,则
,则
![]()
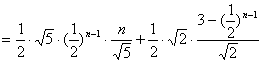
![]()
![]()
∴数列![]() 单调递减
单调递减![]() .∴四边形
.∴四边形![]() 的面积的最大值为
的面积的最大值为![]()
(文)(1)当k=0时,f(x)=-3x2+1,∴f(x)的单调增区间为(-∞,0),单调减区间[0,+∞].
当k>0时 , f '(x)=3kx2-6x=3kx(x-).
∴f(x)的单调增区间为(-∞,0) , [ , +∞], 单调减区间为[0, ].
(2)当k=0时, 函数f(x)不存在最小值.
当k>0时, 依题意 f()= - +1>0 ,
即k2>4 , 由条件k>0, 所以k的取值范围为(2,+∞).
22.(1)从第n年初到第n+1年初,鱼群的繁殖量为axn,被捕捞量为bxn,死亡量为
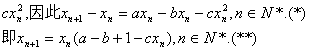
(2)若每年年初鱼群总量保持不变,则xn恒等于x1, n∈N*,从而由(*)式得
![]()
因为x1>0,所以a>b.
猜测:当且仅当a>b,且![]() 时,每年年初鱼群的总量保持不变.
时,每年年初鱼群的总量保持不变.
(3)若b的值使得xn>0,n∈N*
由xn+1=xn(3-b-xn), n∈N*, 知
0<xn<3-b, n∈N*, 特别地,有0<x1<3-b. 即0<b<3-x1.
而x1∈(0, 2),所以![]()
由此猜测b的最大允许值是1.
下证 当x1∈(0, 2) ,b=1时,都有xn∈(0, 2), n∈N*
①当n=1时,结论显然成立.
②假设当n=k时结论成立,即xk∈(0, 2),
则当n=k+1时,xk+1=xk(2-xk)>0.
又因为xk+1=xk(2-xk)=-(xk-1)2+1≤1<2,
所以xk+1∈(0, 2),故当n=k+1时结论也成立.
由①、②可知,对于任意的n∈N*,都有xn∈(0,2).
综上所述,为保证对任意x1∈(0, 2), 都有xn>0, n∈N*,则捕捞强度b的最大允许值是1.
欢迎访问 http://www.k12zy.com