乐山市高中2007届第二次调研考试数学(理)
一、选择题:(每题5分,共60分)
1.已知集合![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.1; B.2; C.1或2; D.8;
2.如果复数![]() 是实数,那么实数m等于( )
是实数,那么实数m等于( )
A.1; B.-1; C. ![]() ; D.
; D. ![]() ;
;
3. 若![]() 展开式中的第5项为常数,则
展开式中的第5项为常数,则![]() 等于( )
等于( )
A.10; B.11; C.12; D.13;
4.已知直线![]() 按向量
按向量![]() 平移后得到直线
平移后得到直线![]() ,且
,且![]() 和圆
和圆![]() 相切,那么m的值为( )
相切,那么m的值为( )
A.9或-1; B.5或-5; C.-7或7; D.-3或-13;
5.不等式![]() 的解集为( )
的解集为( )
A.![]() ;B.
;B. ![]() ;C.
;C.![]() ;D.
;D. ![]()
6. 函数![]() 的图象相邻的两条对称轴之间的距离是( )
的图象相邻的两条对称轴之间的距离是( )
A.![]() ; B.
; B. ![]() ; C.
; C. ![]() ; D.
; D. ![]() ;
;
7.在一个盒子里盛有若干个均匀的红球和白球,从中任取一个球,取到红球的概率为![]() ;若从中任取两个球,取到的全是红球的概率为
;若从中任取两个球,取到的全是红球的概率为![]() ,则盒子里一共有红球和白球( )
,则盒子里一共有红球和白球( )
 A.6个;B.9个;C.24个;D.12个;
A.6个;B.9个;C.24个;D.12个;
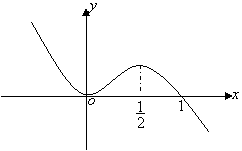
8. 函数![]() 的图象如图所示,
的图象如图所示,
则当![]() 时,
时,
函数![]() 的单调增区间是( )
的单调增区间是( )
A.![]() ;B.
;B. ![]() ;
;
C.![]() ;D.
;D. ![]() ;
;
9.设随机变量![]() 等可能取值1,2,3……,n,如果
等可能取值1,2,3……,n,如果![]() ,那么n的值为( )
,那么n的值为( )
A.3; B.4; C.10; D.9;
10已知数列![]() 满足
满足![]() ,若
,若![]() ,则
,则![]() =( )
=( )
A.3; B.2; C.1; D.-1;
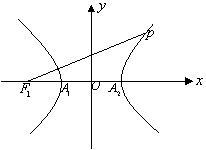 11. 如图,双曲线的左焦点为F1,顶点为
11. 如图,双曲线的左焦点为F1,顶点为![]() ,P是双曲线上任意一点,则分别以线段
,P是双曲线上任意一点,则分别以线段![]() 为直径的两圆位置关系为( )
为直径的两圆位置关系为( )
A.相交;B.相切;C.相离;D.以上情况都有可能;
12. 当![]() 满足条件
满足条件![]() 时,
时,
变量![]() 的取值范围是( )
的取值范围是( )
A.![]() ;B.
;B. ![]() ;C.
;C.![]() ;D.
;D. ![]() ;
;
二、填空题:(每题4分,共16分)
13.已知![]() ,直线
,直线![]() 过点A(3,-1),且与向量
过点A(3,-1),且与向量![]() 垂直,则直线
垂直,则直线![]() 的一般方程为___________
的一般方程为___________
14.已知曲线![]() 在x=-1处的切线与抛物线
在x=-1处的切线与抛物线![]() 相切,则此抛物线的通径长为______
相切,则此抛物线的通径长为______
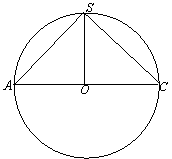 15.已知正四棱锥S-ABCD内接于球O,SAC是过球心O的一个截面,如图所示,若棱锥的底面边长为a,则SC与底面ABCD所成的角的大小为________,球O的表面积为_______
15.已知正四棱锥S-ABCD内接于球O,SAC是过球心O的一个截面,如图所示,若棱锥的底面边长为a,则SC与底面ABCD所成的角的大小为________,球O的表面积为_______
16.关于函数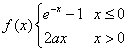 ,(a是常数且a>0)。
,(a是常数且a>0)。
对于下列命题:
① 函数![]() 的最小值是0;②函数
的最小值是0;②函数![]() 在每一点处都连续;
在每一点处都连续;
② 函数![]() 具有反函数;④函数
具有反函数;④函数![]() 在R上是增函数;
在R上是增函数;
⑤函数![]() 具有反函数。
具有反函数。
其中正确命题的序号是_________
三、解答题:共74分。
17.(12分)在△ABC中,三内角A、B、C成等差数列,
向量![]() , ①若
, ①若![]() ;试判断△ABC的形状; ②.记
;试判断△ABC的形状; ②.记![]() ,若关于A的方程
,若关于A的方程![]() 有且仅有一个解,求实数k的取值范围。
有且仅有一个解,求实数k的取值范围。
18.(12分)已知![]() ,等差数列
,等差数列![]() 中,
中,![]() ;
;
①求实数![]() 的值;②求数列
的值;②求数列![]() 的通项公式;③求
的通项公式;③求![]() 的值;
的值;
19.(12分)某足球俱乐部2006年10月份安排4次体能测试,规定:按顺序测试,一旦测试合格就不必参加以后的测试,否则4次测试都要参加,若运动员小李4次测试每次合格的概率组成一个公差为![]() 的等差数列,他第一次测试合格的概率不超过
的等差数列,他第一次测试合格的概率不超过![]() ,且他直到第二次测试才合格的概率为
,且他直到第二次测试才合格的概率为![]() 。
。
①求小李第一次参加测试就合格的概率![]() ;②求小李10月份参加测试的次数
;②求小李10月份参加测试的次数![]() 的分布列和数学期望。
的分布列和数学期望。
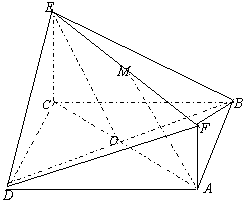
20.(12分)如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=![]() ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。
①.求证:AM∥平面BDE;
②求二面角A-DF-B的大小;
③ 试在线段AC上确定一点P,使得PF与BC所成的角是![]() 。
。
 |
21.(12分)如图所示,点A是椭圆C:![]()
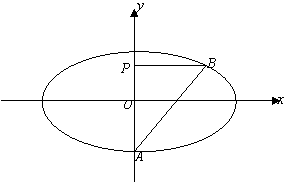 的短轴位于X轴下方的端点,过A作斜率为1的直线交椭圆于B点,P点在Y轴上,且BP∥X轴,
的短轴位于X轴下方的端点,过A作斜率为1的直线交椭圆于B点,P点在Y轴上,且BP∥X轴,![]() 。①若点P的坐标为(0,1),求椭圆C的方程;②若点P的坐标为(0,t),求实数t的取值范围。
。①若点P的坐标为(0,1),求椭圆C的方程;②若点P的坐标为(0,t),求实数t的取值范围。
22.(14)已知函数![]() 是在
是在![]() 上每一点处可导的函数,若
上每一点处可导的函数,若![]() 在
在![]() 上恒成立,①求证:函数
上恒成立,①求证:函数![]() 在
在![]() 上单调递增;
上单调递增;
②求证:当![]() 时,有
时,有![]()
③已知不等式![]() 在
在![]() 时恒成立,
时恒成立,
求证:![]()
参考答案:
一、 选择题:CBCAC;CDDCA;BB;
二、
13.![]() ; 14.32; 15.
; 14.32; 15.![]() ; 16.①②
; 16.①②
三、
17. ①△ABC为等腰三角形;②![]() ;
;
18. ①![]() ; ②
; ②![]() ;
;
③当![]() 时,原式=
时,原式=![]() ; 当
; 当![]() 时,原式=
时,原式=![]()
19.①![]() ;②
;②![]() ; 20.①略;②
; 20.①略;②![]() ;③P点在线段AC上距A点1个单位处;
;③P点在线段AC上距A点1个单位处;
21. .①![]() ;②
;②![]()
22. 略