乐山市高中2007届第二次调研考试数学（文）
一、选择题：（每题5分，共60分）
1.已知全集
，集合A＝
，集合B＝
，则
＝（ ）
A.
； B. 
； C.
； D. 
2.已知
，则“a>b”是“ac>bc”的（ ）
A.充分不必要条件；B.必要不充分条件；C.充要条件；D.既不充分也不必要条件；
3.已知直线x=m和圆相切，那么m的值为（ ）
A.3；B.－1；C.－1或3；D.－3或1；
4.若
展开式中的第5项为常数，则
等于（ ）
A.10；B.11；C.12；D.13；
5.不等式
的解集为（ ）
A.
；B. 
；C.
；D
；
6.若函数
的反函数
，则
的值为（ ）
A.1；B.－1；C.1或－1；D.5；
7.函数
的图象相邻的两条对称轴之间的距离是（ ）
A.
； B. 
； C. 
； D. 
；
8.在等差数列
中，
是前的和，若
，则
的值为（ ）
A.2； B.4； C.11； D.12；
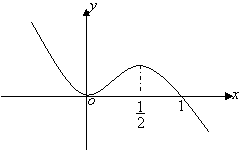
9.函数
的图象如图所示，
则当
时，
函数
的单调增区间是（ ）
A.
；B. 
；
C.
；D. 
；
10一个容量为20的样本数据，分组后，组距与频数如下：
；则样本在
上的频率为（ ）
A.
； B；
； C. 
； D. 
；
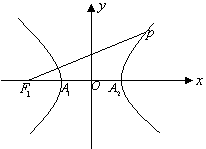11.如图，双曲线的左焦点为F1，顶点为
，P是双曲线上任意一点，则分别以线段
为直径的两圆位置关系为（ ）
A.相交；B.相切；C.相离；D.以上情况都有可能；
12.当
满足条件
时，
变量
的取值范围是（ ）
A.
；B. 
；C.
；D. 
；
二、填空题：（每题4分，共16分）
13.已知
，直线
过点A（3，－1），且与向量
垂直，则直线的一般方程为＿＿＿＿＿＿＿＿＿＿＿
14.已知曲线
在x＝－1处的切线与抛物线
相切，则此抛物线的通径长为＿＿＿＿＿＿
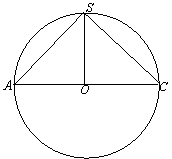15.已知正四棱锥S－ABCD内接于球O，SAC是过球心O的一个截面，如图所示，若棱锥的底面边长为a，则SC与底面ABCD所成的角的大小为＿＿＿＿＿＿＿＿，球O的表面积为＿＿＿＿＿＿＿
16.设函数
，给出如下命题：
①函数必有最小值；②若a＝0时，则函数的值域是R；
③若a＞0时，且的定义域为
，则函数有反函数；
④若函数在区间上单调递增，则实数a的取值范围
是
；
其中正确命题的序号是＿＿＿＿＿＿＿＿＿
（将你认为正确的命题的序号都填上）
三、解答题：（共74分）
17.（12分）已知向量
，记
①求的定义域，值域以及最小正周期；
②若
，其中
，求
；
18.（12分）已知
，等差数列中，
；
①求实数
的值；②求数列的通项公式；③求
的值；
19.（12分）某种电路开关闭合后，会出现红灯或绿灯闪动，已知开关闭合后，出现红灯和绿灯的概率都是
；从开关第二次闭合后，若前次出现红灯，则下一次出现红灯的概率为
，出现绿灯的概率为
；若前次出现绿灯，则下一次出现红灯的概率为
，出现绿灯的概率为
。问：①第二次闭合后出现红灯的概率是多少？②三次发光中，出现一次红灯、两次绿灯的概率是多少？
20.（12分）如图所示，在四棱锥P－ABCD中，PB⊥底面ABCD。CD⊥PD，底面ABCD为直角梯形，AD∥BC，AB⊥BC，AB＝AD＝PB＝3，BC＝6，点E在棱PA上，且PE＝2EA。
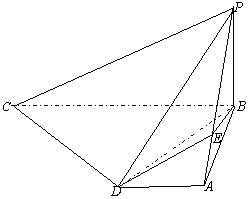①求证：PC∥平面EBD；
②求异面直线PA与CD所成的角；
③求二面角A－BE－D的大小；
21.（12分）如图所示，点A是椭圆C：
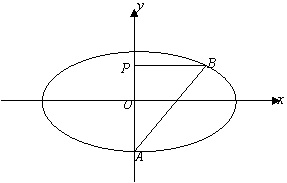的短轴位于X轴下方的端点，过A作斜率为1的直线交椭圆于B点，P点在Y轴上，且BP∥X轴，
。①若点P的坐标为（0，1），求椭圆C的方程；②若点P的坐标为（0，t），求实数t的取值范围。
22.（14分）设定义在R上的函数
，当
时，取得极大值
，且函数
的图象关于Y轴对称，
①求的表达式；②试在函数
的图象上求两点，使以这两点为切点的切线互相垂直，且切点的横坐标都在区间
上；③求证：
；
参考答案：
一、选择题：ADCCD，BCBBD，BB；
二、填空题：13.
； 14.32； 15.
； 16.②③；
三、解答题：
17.①定义域为：
；值域为：
；最小正周期为：
；
②
；
18.①
； ②
；
③当
时，原式＝
； 当
时，原式＝
；
19.①.
； ②. 
；
20.①连接AC交BD于G，连接EG，证PC∥EG即可； ②.
；③. ；
21.①
；②
；
22.①
；②所求两点为（0，0），
或（0，0），
；
③在上最大什为，最小值为
，容易证：
；