江苏省姜堰中学高三数学综合练习(三)
2007.3.
姓名
一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,有且只有一项符合题目要求。)
1.已知命题p:│x+1│>2,命题q: 5x-6<x2,则命题p是命题q的 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2.已知集合M满足M∪{1,2}={1,2,3},则符合条件的集合M的个数为 ( )
A.1个 B.2个 C.3个 D.4个
3.在等待数列{an}中,Sn表示前n项和,且a2+a8=18-a5,则S9= ( )
A.18 B.60 C.54 D.27
4.某公司新聘进8名员工,平均分给下属的甲、乙两个部分,其中两名英语翻译员不能分给同一个部门:另三名电脑编程人员也不能分给同一个部门,则不同的分配方案有( )
A.36种 B.38种 C.108种 D.114种
5.已知函数f(x)=sin(2x+θ)+![]() cos(2x+θ)(0<θ<
cos(2x+θ)(0<θ<![]() =是R上的偶函数,则θ的值为 ( )
=是R上的偶函数,则θ的值为 ( )
![]()
6.设函数![]() 的图象关于直线x=1对称,则f (x)=
(
)
的图象关于直线x=1对称,则f (x)=
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.三棱锥![]() 中:
中:![]() 和
和![]() 是全等的正三角形,边长为2,且
是全等的正三角形,边长为2,且![]() ,则三棱锥
,则三棱锥![]() 的体积为
( )
的体积为
( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
8.设点![]() 为圆
为圆![]() 上的动点,
上的动点,![]() 是圆的切线,且
是圆的切线,且![]() ,则
,则![]() 点的轨迹方程为
( )
点的轨迹方程为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.![]() 是
是![]() 的导函数,
的导函数,![]() 的图象如图所示,则
的图象如图所示,则![]() 的
的
图象只可能是下图中的材 ( )
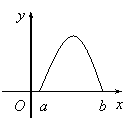
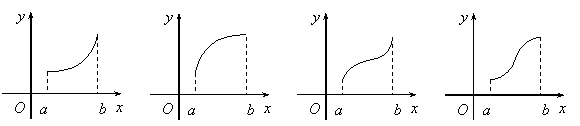
A. B. C. D.
10.对于任意实数x , y ,定义运算![]() ,其中a, b, c为常数,等号右边的运算是通常意义的加、乘运算.现已知1*2=3, 2*3=4,且有一个非零的实数m,使得对任意实数x,都有x* m=x,则m= ( )
,其中a, b, c为常数,等号右边的运算是通常意义的加、乘运算.现已知1*2=3, 2*3=4,且有一个非零的实数m,使得对任意实数x,都有x* m=x,则m= ( )
A.2 B.4 C.6 D.8
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡中相应的横线上.
11.将容量为50的样本数据,按从小到大的顺序分成4组,如下表:
| 组号 | 1 | 2 | 3 | 4 |
| 频数 | 11 | 14 | 13 |
则第3组的频率为
![]()
12.已知向量![]() ,直线
,直线![]() 过点
过点![]() 且与向量
且与向量![]() 垂直,则直线
垂直,则直线![]() 的方程为
的方程为
13.若(![]() )12的展开式中常数项是-220,则实数的a值为
。
)12的展开式中常数项是-220,则实数的a值为
。
14.旅游公司为3个旅游团提供4条线路,每个旅游团任选其中一条. 则恰有2条线路没有被选择的概率为 。
15.已知函数y=f(x)的反函数为y=1+loga(1-x)(a>0,且a≠1),则函数y=f (x)的图象必过定点 。
16.设有四个条件,其中能推出不重合平面α∥β的条件有 (填写所有正确条件的代号)
①平面r与平面α、β所成的锐二面角相等;
②直线a∥平面α,且直线a∥平面β;
③直线a⊥平面α,且直线a⊥平面β;
④a、b是异面直线,aα,bβ,且a∥β,b∥α
三.解答题
17.(本小题满分12分)已知![]() 三个顶点分别是A(1,0)、B(0,1)、C
三个顶点分别是A(1,0)、B(0,1)、C![]() ,其中
,其中![]() .
.
(1)若![]() ,求角
,求角![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
20.(本小题满分14分)函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线平行于直线
处的切线平行于直线![]() ,若函数
,若函数![]() 在
在![]() 时有极值.
时有极值.
(1)求![]() ,
,![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3) 若函数![]() 在区间
在区间![]() 上的的最大值为10,求
上的的最大值为10,求![]() 在该区间上的最小值.
在该区间上的最小值.
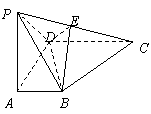
19.(本题满分14分)如图:四棱锥![]() 底面为一直角梯形,
底面为一直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 面
面![]() ,
,![]() 为
为![]() 中点.
中点.
(1)求证:平面![]() 平面
平面![]()
(2)求证:![]() ∥平面
∥平面![]()
(3)假定![]() .求二面角
.求二面角![]() 的平面角的正切值.
的平面角的正切值.
 |
20.(本小题满分15分)已知点A(1,0),B(0,1),C(1,1)和动点P(x,y)满足![]() 的等差中项.
的等差中项.
(1)求P点的轨迹方程;
(2)设P点的轨迹为曲线C1按向量![]() 平移后得到曲线C2,曲线C2上不同的两点M,N的连线交y轴于点Q(0,b),如果∠MON(O为坐标原点)为锐角,求实数b的取值范围;
平移后得到曲线C2,曲线C2上不同的两点M,N的连线交y轴于点Q(0,b),如果∠MON(O为坐标原点)为锐角,求实数b的取值范围;
(3)在(2)的条件下,如果b=2时,曲线C2在点M和N处的切线的交点为R,求证:R在一条定直线上.
21.(本小题满分15分)已知定义在R上的单调函数![]() ,存在实数
,存在实数![]() ,使得对于任意实数
,使得对于任意实数![]() 总有
总有![]() 恒成立.
恒成立.
(1)求x0的值.
(2)若![]() ,且对任意正整数n,有
,且对任意正整数n,有![]() ,记
,记
![]() ,比较
,比较![]() 与Tn的大小关系,并给出证明;
与Tn的大小关系,并给出证明;
(3)若不等式![]() 对任意不小
对任意不小
于2的正整数n都成立,求x的取值范围.
答案
一.选择题 DD CAA BB D D B
二.填空题
11.0.24 12.![]() 13.1 14.
13.1 14.![]() 15.(1,0) 16.③④
15.(1,0) 16.③④
三.解答题
17.解:(1)∵![]() 三个顶点分别是A(1,0)、B(0,1)、C
三个顶点分别是A(1,0)、B(0,1)、C![]() ,
,
∴![]()
∵![]() ∴
∴![]() ∴
∴![]()
∵![]() ∴
∴![]()
(2)由![]() ,得:
,得:![]()
即 ![]() ,
,
∴ ![]() ,
,![]()
![]()
又 ![]() , ∴
, ∴![]() ,
,![]() ∴
∴ ![]() .
.
18.(1) ![]() =2,,
=2,,![]() =-4
=-4
(2)函数![]() 的单调增区间为:(-∞,-2)(
的单调增区间为:(-∞,-2)(![]() ,+∞)单调增区间为:(-2,
,+∞)单调增区间为:(-2,![]() )
)
(3) 由函数![]() 在区间
在区间![]() 上的的最大值为10,得c=2
上的的最大值为10,得c=2
![]() 在该区间上的最小值为:
在该区间上的最小值为:![]()
19.(1)证明:![]() 面
面![]()
![]()
![]() 且
且![]()
![]() 面
面![]()
![]()
![]()
(2)证明:取![]() 的中点
的中点![]() ,连接
,连接![]()
![]() ,
,![]() 在
在![]() 中:
中:![]()
![]()
![]()
![]() ∴
∴![]()
![]()
![]()
![]()
∴四边形![]() 为平行四边形,即
为平行四边形,即![]() ∥
∥![]()
∵![]() 面
面![]() 且
且![]() 面
面![]() ∴
∴![]() ∥平面
∥平面![]()
(3)解:连接![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() .
.
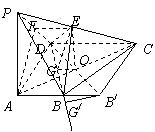 在
在![]() 中:
中:![]()
![]()
![]()
![]()
![]() 面
面![]()
过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() 。
。
由三垂线定理知:![]() 为所求二面角
为所求二面角![]() 的平面角 设
的平面角 设![]()
连![]() 并延长交
并延长交![]() 于
于![]() ,则四边形
,则四边形![]() 为正方形,且
为正方形,且![]() 为
为![]() 中点,过
中点,过![]() 作
作![]() 交
交![]() 于
于![]() .
.
![]()
![]() 在
在![]() 中:
中: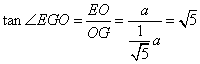
故:二面角![]() 的平面角的正切值为
的平面角的正切值为![]()
20.(1)由题意可得![]() 则
则
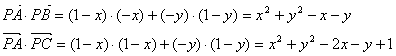
又![]() 的等差中项
的等差中项
![]()
整理得点![]() 的轨迹方程为
的轨迹方程为![]()
(2)由(1)知![]()
又![]() 平移公式为
平移公式为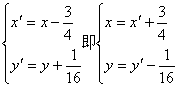 ,代入曲线C1的方程得到曲线C2的方程为:
,代入曲线C1的方程得到曲线C2的方程为:![]() 即
即![]()
曲线C2的方程为![]() . 如图由题意可设M,N所在的直线方程为
. 如图由题意可设M,N所在的直线方程为![]() ,
,
由 令
令
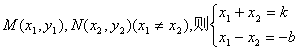 点M,N在抛物线上
点M,N在抛物线上![]()
![]()
又![]() 为锐角
为锐角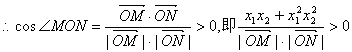
![]() ………10分
………10分
(3)当b=2时,由(2)可得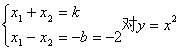 求导可得
求导可得![]()
![]() 抛物线C2在点
抛物线C2在点![]() 处的切线的斜率分别为
处的切线的斜率分别为![]() ,
,
![]() 在点M、N处的切线方程分别为
在点M、N处的切线方程分别为
![]()
由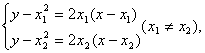 解得交点R的坐标
解得交点R的坐标![]()
满足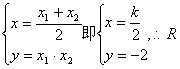 点在定直线
点在定直线![]() 上
上
21.(本小题满分14分)
解:(1)令![]() ,得
,得![]() ①
①
令![]() ,得
,得![]() ②
②
由①,②得 ![]()
![]() 为单调函数, ∴
为单调函数, ∴![]()
(2)由(1)得![]() ,
,
![]()
![]()
![]()
又![]()
![]()
又![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
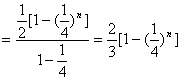
![]()
![]() ,
,
![]()
(3)令![]() ,
,
则![]()
∴当![]() 时,
时,![]()
![]() 即
即![]()
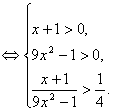 解得
解得![]() 或
或![]()