高三数学联合考试

南通四县市2007届高三联合考试（数学）　　　　　　　　　　　　　　　　　　　　

一、选择题：　　　　　　　　　　　　　　　　　　　　　　　　　　  2007年3月1日

1、在上，函数与函数具有

A、相同的单调性　　B、相同的周期性　　C、相同的奇偶性　　　D、相同的值域

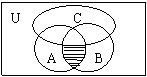2、右图中阴影部分可表示

A、　　　　B、　　
　　C、　　D、

3、已知两圆方程分别为：，，则两圆的公切线方程为

A、　　B、　　C、　　  D、

4、若，则函数与的图象关于

A、直线对称　B、轴对称　　　　C、原点对称　　　　  D、轴对称

5、在的展开式中，含的正奇数指数幂的项数共有

A、1项　　　　　  B、2项　　　　　　 C、3项　　　　　　  D、4项

6、班上要选派5名爱好书法的同学中的3名参加校外书法培训，共3期（每期只派1名，不能重复选派），由于时间上的冲突。甲、乙两位同学都不能参加第1期培训，则不同的选派方法有

A、12种　　　　　 B、24种　　　　　  C、36种　　　　　　 D、48种

7、要得到函数的图象，只需将函数的图象

A、向左平移个单位长度，再横坐标不变纵坐标伸长到原来的2倍
B、向右平移个单位长度，再横坐标不变纵坐标伸长到原来的倍
C、向左平移个单位长度，再横坐标不变纵坐标伸长到原来的2倍
D、向右平移个单位长度，再横坐标不变纵坐标伸长到原来的倍

8、某幼儿园举行讲故事、唱歌、跳舞、写字比赛，凡有一项优胜，则奖励一朵小红花。李云水同学跳舞一定优胜；讲故事、写字有一半的把握优胜；唱歌有七成把握优胜。则李云水能获得不少于三朵小红花的概率为

A、0.175　　　　　 B、0.250　　　　　  C、0.425　　　　　　 D、0.600

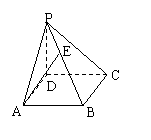9、如图，垂直正方形所在的平面，，动点在线段上，则二面角的取值范围是

A、　　　 B、　
C、　　　　　　　　  D、

10、若是上的增函数，且，，设，，若“”是“”的充分不必要条件，则实数的取值范围是

A、　　　　 B、　　　　　 C、　　　　 D、

二、填空题：

11、若，则________

12、某同学在期中考试中，语文、数学、英语、物理、化学成绩（单位：分）分别为：100，，，90，80。已知该同学各科的平均分为100，方差为200，则数学成绩为______分

13、已知函数，若在处的导数值为20，则______

14、半径为3的四个铁球熔解后铸成一个长方体（不计损耗），其中长方体的一条边长为4，则该长方体的表面积最小值为_________

15、已知动点满足，为坐标原点，则的取值范围是_______

16、对正整数，设抛物线，过任作直线交抛物线于，两点，则数列的前项和为__________

三、解答题：

17、在中，已知，外接圆半径为5
（1）求的大小；（2）若，求的周长。
18、某上市股票在30天内每股的交易价格（元）与时间（天）所组成的有序数对，点　
　 落在下图中的两条线段上；该股票在30天内的日交易量（万股）与时间（天）的部分数　
　 据如下表所示：

第t 天	4	10	16	22
（万股）	36	30	24	18

（1）根据提供的图象，写出该种股票每股交易价格（元）与时间（天）所满足的函数关系式；
（2）根据表中数据确定日交易量（万股）与时间（天）的一次函数关系式；
（3）用表示该股票日交易额（万元），写出关于的函数关系式，并求在这30天中第几天日　　
　　 交易额最大，最大值是多少？

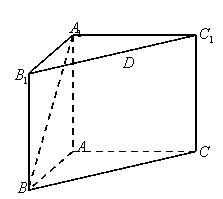
19、在直三棱柱中，，，且异面直线与所成的角为，

（1）求的值；
（2）设是上的任意一点，求点到平面的距离；
（3）请根据下面要求设计一种切割和拼接方法。要求用平行于侧棱的平面去截此三棱柱，切开后　
　　 的两个几何体再拼接成一个直四棱柱，而且所得四棱柱的表面积小于原三棱柱的表面积。（简　
　　 明扼要地写出切割方法、拼接方法，并计算拼接后四棱柱的表面积）

20、设，分别是椭圆的左，右焦点。

（1）当，点在椭圆上，且，时，求椭圆方程；
（2）对于（1）中的椭圆，若直线分别交椭圆于两点，设椭圆的长轴顶点分别　　　　
　　为，，求直线与交点的轨迹方程；

（3）过（2）中轨迹的一个焦点作直线与轨迹交于，两点，若，这样的直线能作几条？并证明你的结论？

21、已知数列是由正数组成的等比数列，是其前项的和。

（1）当首项，公比时，对于任意的正整数及正数都有成立，求的取值范围；

（2）是否存在正常数，使得成立？并证明你的结论。

南通四县市2007届高三联合考试数学试题参考答案

一、选择题：

BDACB　CADAD

二、填空题：

11.—  12.120或110　 13. 　　14. 72π+96　 15. [,]　　16. –n(n+1)

三、解答题：

17.解：（1）由正弦定理得sinA= = ∵∠A∈(0, π) ∴∠A= 或

(2) ∵,　∴∠A= ,bc=11

由余弦定理得=,即(b+c)² =3bc+75=108, ∴b+c=6,所以三角形周长为11。

18．解（1）,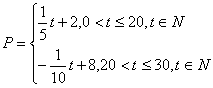　

(2)　

(3)　

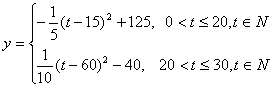
当时，万元，当，y随t的增大而减小

答：在30天中的第15天，日交易额取得最大值125万元。

19、解：（1）连结A₁C，∵ABC-A₁B₁C₁是直三棱柱，且AB=AC=1，∴A₁B=A₁C=

B₁C₁//BC即∠A₁BC就是异面直线A₁B与B₁C₁所成的角为60°，从而得△A₁BC为等边三角形。又∠BAC=90°∴BC==,得a=1.

(2)取B₁C₁、BC的中点F、E，连A₁F，FE，A₁E，得△A₁EF，由B₁C₁//BC，BC平面A₁BC，B₁C₁在平面外，∴B₁C₁//平面A₁BC，即D 到平面A₁BC的距离就是F到平面A₁BC的距离。

由上可知BC⊥A₁E，BC⊥FE，可得平面A₁BC⊥A₁EF，且相交于A₁E，故F到平面A₁BC的距离就是F到直线A₁E的距离。在Rt △A₁Ef中，易得所求值为.

(3)原三棱柱表面积为3+

以A₁C₁，B₁C₁的中点G，F所在的直线向下切开，使C₁与B₁重合，拼成一个以1，为边长的长方形，此时表面面积为4<3+.\

20.解：（1）∵a=2b,a²=b²+c²,∴c²=3b².　又∵PF₁⊥PF₂，∴PF₁²+PF₂²=（2C）²=12b².

由椭圆定义可知PF₁+PF₂=2a=4b,( PF₁+PF₂)²=12b²+4=16b²,从而得b²=1,a²=4,椭圆方程为。

（2）由题意得：A₁（-2，0），A₂（2，0），P（t,）,Q(t, — )，

得A₁P方程y= (x+2) , A₂Q方程y= — (x-2)，两式相乘得y²= (x²-4)

得（y0）(3)答：能作三条。

证明：过双曲线左焦点F（— ,0）,当直线垂直x轴时AB=1< 4,故直线不垂直于x轴。设直线y=k(x+),代入双曲线方程消去y并整理得

AB=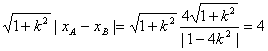

解得k=0,k=,故有三条。

21．解（1）由S_k=4(1-)　得S_k+1=S_k+2,代入 得或对于任意正整数k成立，由单调性可知S₁S_k<4得2S_k<4，所以或c<1故0<c<1

(2)假设存在一个正常数m满足题意，

则有：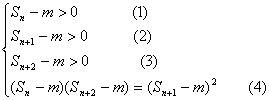

由（4）得

即，又因为m>0,故

当q=1（a₁>0,q>0）时

当时，

即q>0 时，有所以不成立。

故不存在正常数m，使得成立。