上海市十一所实验示范校07高三联考数学(文)2007.3.15
1.设![]() = 。
= 。
2.点P(x,y)满足:![]() ,那么点P的轨迹为
。
,那么点P的轨迹为
。
3.函数![]() 的值域为
。
的值域为
。
4.过点A(2,4),且切y轴于点B(0,2)的圆方程为 。
5.梯形ABCD中,![]() 。设E,F分别是BC和CD的中点,则用
。设E,F分别是BC和CD的中点,则用![]() 表示向量
表示向量![]() 为
。
为
。
6.已知点P(x,y)的坐标满足条件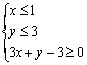 ,那么Z=x-y的取值范围是
。
,那么Z=x-y的取值范围是
。
7.函数![]() 的图象关于直线x=2对称,则b=
。
的图象关于直线x=2对称,则b=
。
8.在等差数列![]() 中,公差d等于2,又
中,公差d等于2,又![]() 则
则
![]() =
。
=
。
9.对任意函数![]() 在其公共定义域内,规定
在其公共定义域内,规定![]() 若
若
![]() 的最大值为
。
的最大值为
。
| |
11.坐标平面上点(7,5)处有一光源,将圆![]() 投射到x轴所得的影长为
。
投射到x轴所得的影长为
。
12.已知函数![]() 满足:对任意的
满足:对任意的![]() ,当
,当![]() 时,总有
时,总有![]() 的取值范围是
。
的取值范围是
。
13.对任意直线l,平面上必有直线m,使m与l成为( )
A.平行直线 B.相交直线 C.垂直直线 D.异面直线
14.某次求职考试,试卷内只有5个单选题,满分100分,每题答对时得20分,答错得0分,不倒扣分,阅卷完毕后,考评组公布了每题的答对率如下:
题号 一 二 三 四 五
答对率 81% 66% 60% 48% 45%
问此次考试,全体求职人员的平均分为 ( )
A.70分 B.65分 C.60分 D.55分
15.函数![]() 在区间A上是递增函数,那么区间A为( )
在区间A上是递增函数,那么区间A为( )
A.(-∞,0) B.![]() C.
C.![]() D.
D.![]()
16.已知数列![]() 的通项公式
的通项公式![]() 设其前n项和为Sn,则能够使Sn<-5成立的正整数n( )
设其前n项和为Sn,则能够使Sn<-5成立的正整数n( )
A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
17.已知复数![]()
(1)设复数![]()
(2)当复数z满足z=1,求z-z1的最大值。
18.设数列{an}的通项公式为![]()
(1)写出数列{an}的前7项。
(2)当![]() 时,证明k2-k必为偶数。
时,证明k2-k必为偶数。
(3)设k为一正整数,证明在数列{an}中,必可找到某项am,使am=k。
19.已知:![]()
(1)求![]() 的值。
的值。
(2)设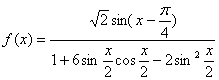 ,解关于x的方程:
,解关于x的方程:![]()
|
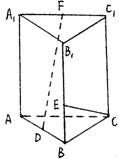
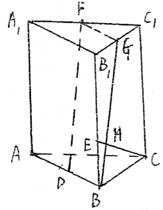
(1)求异面直线DF和CE所成角的大小。
(2)设P为BB1上的动点,问当BP的长度为多少时,
CP和DF垂直。
21.已知二次函数![]() 满足:对任意实数x,都有
满足:对任意实数x,都有![]() ,且当
,且当![]() (1,3)时,有
(1,3)时,有![]() 成立。
成立。
(1)证明:![]() 。
。
(2)若![]() 的表达式。
的表达式。
(3)设![]()
![]() ,若
,若![]() 图上的点都位于直线
图上的点都位于直线![]() 的上方,求实数m的取值范围。
的上方,求实数m的取值范围。
22.(1)数列{an}和{bn}满足![]() (n=1,2,3…),求证{bn}为等差数列的充要条件是{an}为等差数列。(8分)
(n=1,2,3…),求证{bn}为等差数列的充要条件是{an}为等差数列。(8分)
(2)数列{an}和{cn}满足![]() ,探究
,探究![]() 为等差数列的充分必要条件,需说明理由。[提示:设数列{bn}为
为等差数列的充分必要条件,需说明理由。[提示:设数列{bn}为![]() ]
]
1.![]() 2.线段 3.(1,+∞) 4.
2.线段 3.(1,+∞) 4.![]()
5.![]() 6.[-3,1] 7.18 8.2 9.1 10.
6.[-3,1] 7.18 8.2 9.1 10.![]() 11.
11.![]()
12.![]()
二、选择题
13.C 14.C 15.B 16.A
三、解答题
17.解:(1)![]() ………………2分
………………2分
∵![]() …………2分
…………2分
∴![]() …………2分
…………2分
(2)解法1:令t=z-z1=1,则z=t+z1
∵z=1,∴t+2-2i=1 …………2分
复数t对应的点在圆心为-2+2i,半径为1的圆周上 …………2分
∴t最大=-2+2i+1=2![]() +1
+1
即z-z1最大=2![]() +1 …………2分
+1 …………2分
解法2:设![]()
![]()
令![]()
上式![]()
∴![]()
解法3:前面如同(2),![]()
令![]() ∵a,b满足a2+b2=1
∵a,b满足a2+b2=1
利用线形规划的数学方法,也可以求出![]()
∴![]()
用解法2,或者解法3的方法解题,各步骤具体得分参考解法1标准给分。
18.解:(1)![]() ;
;![]()
(2)∵![]() 时。k与k-1为一奇数和一偶数
时。k与k-1为一奇数和一偶数
∴![]() 必为偶数,命题得证
必为偶数,命题得证
(3)设k为正整数
要使![]() , 只要
, 只要![]() …………2分
…………2分
8n-7=4k2-4k+1
即 ![]() …………2分
…………2分
由(2)的证明可知 ![]() 必为正整数,设为t,则取m=t+1 …………2分
必为正整数,设为t,则取m=t+1 …………2分
∴数列中存在一项am,使得 ![]()
19.解:(1)∵![]() ∴
∴![]()
解出 ![]() …………2分
…………2分
∵![]() ,
,![]() …………2分
…………2分
∴![]() …………2分
…………2分
(2)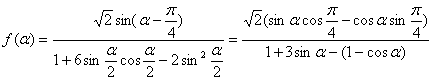 ……2分
……2分
![]() …………2分
…………2分
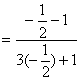
=3 …………2分
∴![]()
∴![]() …………2分
…………2分
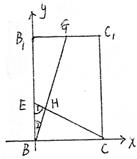
20.解:(1)取B1C1中点G,连FG,BG,又BG交EC于H
|
∴FG平行且相等于DB
∴FGBD为平行四边形, ∴FD//GB,
异面直线DF与CE所成的角为∠EHB在
侧面B1C上,如图建立坐标系
∵E(0,1),C(4,0),∴![]()
∵B(0,0),G(2,3),∴![]()
∴![]()
|
解法2:图中![]() ,
,
∴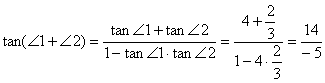
而![]()
∴异面直线DF与CE所成的角为![]()
(2)如(1),利用建立坐标系的方法,设![]() ……2分
……2分
![]() …………2分
…………2分
要使得![]() ,即8-3x=0,∴
,即8-3x=0,∴![]() …………2分
…………2分
∴当BP=![]() 时,CP与DF垂直
时,CP与DF垂直
21.解:(1)由条件知 ![]() 恒成立
恒成立
又∵取x=2时,![]() 与恒成立
与恒成立
∴![]() …………4分
…………4分
(2)∵![]() ∴
∴![]() ∴
∴![]() ……2分
……2分
又
![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
∴![]() , …………2分
, …………2分
解出:![]()
∴![]() …………2分
…………2分
(3)由分析条件知道,只要![]() 图象(在y轴右侧)总在直线
图象(在y轴右侧)总在直线 ![]() 上方即可,也就是直线的斜率
上方即可,也就是直线的斜率![]() 小于直线与抛物线相切时的斜率位置,于是:
小于直线与抛物线相切时的斜率位置,于是:
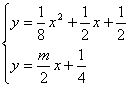 利用相切时△=0,解出
利用相切时△=0,解出 ![]() …………4分
…………4分
∴![]() …………2分
…………2分
解法2:![]() 必须恒成立
必须恒成立
即
![]() 恒成立
恒成立
①△<0,即 [4(1-m)]2-8<0,解得:![]() ……2分
……2分
②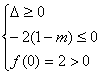 解出:
解出:![]() …………2分
…………2分
总之,![]()
22.证明:(1)必要性 若{bn}为等差数列,设首项b1,公差d
则![]()
∵![]() ∴{an}为是公差为
∴{an}为是公差为![]() 的等差数列 ……4分
的等差数列 ……4分
充分性 若{an}为等差数列,设首项a1,公差d
则![]()
![]()
∴![]()
当n=1时,b1=a1也适合
∵bn+1-bn=2d, ∴{bn}是公差为2d的等差数列 …………4分
(2)结论是:{an}为等差数列的充要条件是{cn}为等差数列且bn=bn+1
其中![]() (n=1,2,3…) …………4分
(n=1,2,3…) …………4分