江苏省南菁高级中学07年高三数学试卷
一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.
1、设
Ａ、[2，4] Ｂ. 
Ｃ. [－2，4] Ｄ. 
、
2、给出以下三个命题：
（1）垂直于同一条直线的两个平面平行
（2）与一个平面等距离的两点的连线一定平行于这个平面
（3）“一个平面内有无数条直线与另一个平面平行”是“两个平面平行”的充分不必要条件. 其中正确的命题的个数有
A. 0个 B、1个 C、2个 D、3个
3、已知
，则
Ａ. 在区间(-1,+∞)上是增函数 Ｂ. 在区间(-∞,1) 上是增函数
Ｃ. 在区间(-1,+∞)上是减函数 Ｄ. 在区间(-∞,1) 上是减函数
4、已知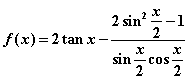
，则
的值为
Ａ. 
Ｂ. 
Ｃ. 4 Ｄ. 8
5、若平面四边形ABCD满足
，
，则该四边形一定是
A. 直角梯形
B. 矩形
C. 菱形
D. 正方形
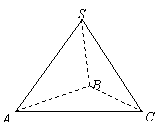
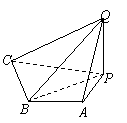
6、如图，正三棱锥
中，侧面
与底面
所成的二面角
等于
，动点
在侧面内，
底面，垂足为
，
，则动点的轨迹为
Ａ. 线段 Ｂ. 圆
Ｃ.一段圆弧 Ｄ.一段抛物线
7、已知数列
为等比数列，
，又第
项至第
项的和为112
，
则
的值为
A. 11 B. 12 C. 13 D. 14
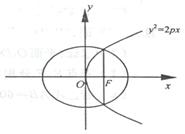8、如图，已知抛物线
的焦点恰好是
椭圆
的右焦点
，且两条曲线的连线过
，则该椭圆的离心率为
Ａ. 
Ｂ. 
Ｃ. 
Ｄ.
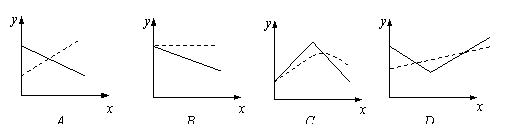9、在股票买卖过程中，经常用到两种曲线，一种是即时价格曲线
（实线表示），另一种是平均价格曲线
（虚线表示）(如f (2)
= 3是指开始买卖后二个小时的即时价格为3元；g (2) = 3表示二个小时内的平均价格为3元)，下图给出的四个图像中，其中可能正确的是
 |
10、已知
是定义
在上的偶函数，对任意
，都有
，若
，则
等于
A． 2007 B． 2006 C． 2 D．0
二、填空题：本大题共6小题，每小题5分，共30分。把答案填写在答题卡相应位置上
11、已知甲、乙两家工厂上半年每月工业生产产值如下表：（单位：万元）
| 月份 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲厂 | 70 | 50 | 80 | 40 | 65 | 55 |
| 乙厂 | 55 | 65 | 55 | 65 | 55 | 65 |
试问哪一家工厂生产情况更平稳、正常 ▲ ．（填甲或乙）
12、
的展开式的第4项是 ▲ ．
13、球面上有A，B，C三点，AB=
，BC=
，CA=6，若球心到平面ABC的距离为4，则球的表面积是 ▲ ．
14、已知向量
，其夹角为
，则直线
=0与圆
的位置关系是 ▲ ．
15、已知函数
，则
的图象的交点个数为 ▲ ．
16、一台仪器每启动一次都随机地出现一个10位的二进制数
，其中A的各位数字中，
，
出现0的概率为
，出现1的概率为
，记
,当启动仪器一次时．则
，且有且仅有3个1连排在一起时为的概率为 ▲ ．
三、解答题：本大题共5小题，共70分。解答应写出文字说明、证明过程或演算步骤。
17、（本题满分14分，第1小问7分，第2小问7分）
已知A、B、C三点的坐标分别是A(3,0)、B（0，3）、C（cos,sin）,其中
。
（1）若
，求角的值；
（2）若
,求
的值。
18、（本小题满分14分，第一小问满分3分，第二小问满分5分，第三小问满分6分）
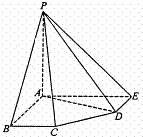在五棱锥P-ABCDE中，PA=AB=AE=2a，PB=PE=
a，BC=DE=a，∠EAB=∠ABC=∠DEA=90°．
（1）求证：PA⊥平面ABCDE；
（2）求二面角A-PD-E的大小；
（3）求点C到平面PDE的距离．
19、（本题满分14分，第1小问9分，第2小问5分）
神舟六号飞船返回舱顺利到达地球后，为了及时将航天员安全救出，地面特别指挥中心在返回舱到达区域安排三个求援中心（记为A、B、C），A在B的正东方向，相距6千米，C在B的北偏西30°，相距4千米，P为航天员着陆点，某一时刻，A接受到P的求救信号，由于B、C两地比A距P远，因此4秒后，B、C两个求援中心同时接受到这一信号．已知该信号的传播速度为1千米/秒．
⑴ 求在A处发现P的方位角；
⑵ 若信号从P点的正上空Q点处发出，则A、B收到信号时间差变大还是变小，说明理由．
20、（本题满分14分，第1小问5分，第2小问9分）
当实数
变化时,直线
与直线
都过同一定点。
(Ⅰ) 求点
所在曲线C的方程;
(Ⅱ)设M为曲线C的准线上一点，A,B为曲线C上两点.若AB所在直线过曲线C的焦点,那么△
能否为正三角形?若能,求出直线AB的方程;若不能,请说明理由.
21、（本题满分14分，第1小问6分，第2小问8分）
设函数f（x）的定义域为R，当x＜0时，f（x）＞1，且对任意的实数x，y∈R，有
f（x+y）=f（x）f（y）
（Ⅰ）求f（0），判断并证明函数f（x）的单调性；
（Ⅱ）数列{an}满足a1=f（0），且
①求{an}通项公式。
②当a＞1时，不等式
对不小于2的正整数恒成立，求x的取值范围。
江苏省南菁高级中学高三数学试卷参考答案
一、选择题：本大题共10小题，每小题5分，共50分
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | B | D | D | C | D | B | A | C | C |
二、填空题：本大题共6小题，每小题5分，共30分
11、
乙；
12、
；
13、
；
14、相离；
15、4；
16、
三、解答题：本大题共5小题，共70分
17、解：
，
，
，
，
，
………… 7分
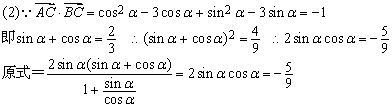
………… 14分
18、（1）证明∵PA=AB=2a，PB=2
a,∴PA2+AB2=PB2，∴∠PAB=90°，即PA⊥AB．
同理PA⊥AE．3分∵AB∩AE=A，∴PA⊥平面ABCDE． …………… 3分
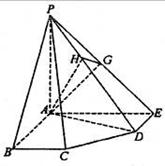（2）∵∠AED＝90°，∴AE⊥ED．
∵PA⊥平面ABCDE，∴PA⊥ED．
∴ED⊥平面PAE．过A作AG⊥PE于G，
∴DE⊥AG，∴AG⊥平面PDE．
过G作GH⊥PD于H，连AH，
由三垂线定理得AH⊥PD．
∴∠AHG为二面角A-PD-E的平面角．
………… 6分 在直角△PAE中，AG＝a．在直角△PAD中，AH＝
a，
∴在直角△AHG中，sin∠AHG＝
＝
．∴∠AHG＝arcsin．
∴二面角A-PD-E的大小为arcsin． …………… 8分
（3）∵∠EAB=∠ABC=∠DEA=90°, BC=DE=a,AB=AE=2a,
取AE中点F，连CF，
∵AF∥=BC, ∴四边形ABCF为平行四边形．
∴CF∥AB，而AB∥DE， ∴CF∥DE，而DE
平面PDE，CF
平面PDE，
∴CF∥平面PDE．
∴点C到平面PDE的距离等于F到平面PDE的距离． ……………10分
∵PA⊥平面ABCDE， ∴PA⊥DE． 又∵DE⊥AE，∴DE⊥平面PAE．
∴平面PAE⊥平面PDE．
∴过F作FG⊥PE于G，则FG⊥平面PDE．
∴FG的长即F点到平面PDE的距离． ……………12分
在△PAE中，PA=AE=2a，F为AE中点，FG⊥PE，
∴FG=
a． ∴点C到平面PDE的距离为a．
…………… 14分
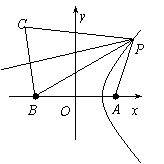19、解：⑴ 如图所示，∵PB＝PC，∴P在线段BC的垂直平分线上，
又∵PB－PA＝4，∴P在以A、B为焦点的双曲线的右支上，
以AB中点为坐标原点，AB所在直线为x轴建立直角坐标系，
则A(3，0)，B(－3，0)，C(－5，2)，
∴双曲线方程为－＝1，（x＞0）， …………… 5分
BC的垂直平分线方程为x－y＋7＝0， …………… 7分
∴P(8，5)，kPA＝tan∠PAx＝，∠PAx＝60°，
∴P点在A点的北偏东30°处．
…………… 9分
⑵ 如图所示，设PQ＝h，PB＝x，PA＝y，
∵－＝－＝(x－y)
＜x－y＝－，
故A、B收到信号时间差变小，B、C两个求援中心收到信号的时间少于4秒．…14分
20、解：（Ⅰ）由
得
∴
解得x=-2，y=3 , 直线
过定点（-2，3） ------------2分
由点（-2，3）在直线
：
上得
∴
即点P(m，n)所在的曲线C的方程为
--------------------5分
（Ⅱ）曲线C的焦点F(1，0），准线为x=
，
当AB与x轴垂直时显然△ABM不能为正三角形，
故设直线AB斜率为k（k≠0）， 设A(x1，y1)，B(x2，y2)
直线AB方程：y=k(x-1)代入得 
， 
线段AB中点N(
),
-----------------8分
∵MN⊥AB，∴直线MN方程:
将x=-1代入得点M坐标
---------------------11分
由△ABM为正三角形得
=
，解得
--------------------13分
∴△ABM能为正三角形，直线AB的方程为
.
-----------------------14分
21、解：（Ⅰ）
时，f（x）＞1
令x=－1，y=0则f（－1）=f（－1）f（0）∵f（－1）＞1
∴f（0）=1 ……………………………2分
若x＞0，则f（x－x）=f（0）=f（x）f（－x）故
故x∈R f（x）＞0 ……………………………………4分
任取x1＜x2 
故f（x）在R上减函数 …………………………6分
（Ⅱ）①
由f（x）单调性知，an+1=an+2 故{an}等差数列 
………………9分
②
是递增数列
…………11分
当n≥2时，
|
…………………12分
即
而a＞1，∴x＞1
故x的取值范围（1，+∞） ……………………14′