厦门双十中学2007届高三年级阶段测试
数学试题（文）
一、选择题：（每小题5分，共60分）
1. 设全集是实数集R，M=
等于 （ ）
A. {xx<-2} B. {x-2<x<1} C. {xx<1或x>2} D. {x-2≤x<1}
2．点（2，-1）沿向量
平移到（-2，1），则点（-2，1）沿平移到 （ ）
A.（2，-1） B.（-2，1） C.（6，-3） D.（-6，3）
3．已知函数
，则
（ ）
A．0 B．1
C．3
D．
4．等比数列
，若
，则数列前12项和S12为（ ）
A．－50 B．
C．
D．
5．函数
是 （ ）
A．最小正周期是π的偶函数 B．最小正周期是π的奇函数
| |
6．若曲线
在点P处的切线平行于直线3x-y＝0，则点P的坐标为 （ ）
A．（1，3） B．（-1，3） C．（1，0） D．（-1，0）
7．函数
与
图像关于直线x－y＝0对称，则
的单调增区间是 （ ）
A．（0，2） B．（-2，0） C．（0，＋∞） D．（-∞，0）
|
若f(1)＞1，
，则 （ ）
A．
B．且a≠－1
C．
D．
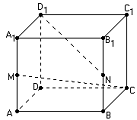
9．如图，在正方体
中，M、N分别为棱
和
中点，则异面直线CM与
所成角的正弦值为 （ ）
A．
B．
C．
D．
10．已知抛物线
的焦点弦
的两端点为
，
，则关系式
的值一定等于 （ ）
|
11．过圆
内点P
有n条弦，这n条弦的长度成等
差数列
，如果过P点的圆的最短的弦长为a1，最长的弦长
为an，且公差
，那么n的取值集合为 （ ）
A．{5，6，7} B．{4，5，6} C．{3，4，5} D．{3，4，5，6}
12．A、B是椭圆
（a>b>0）的左右顶点，C、D是左焦点F的通经端点.过F作垂直与椭圆所在平面的垂线l，且P为l上一点，则四棱锥P—ABCD的侧棱中的最短侧棱 （ ）
A．是PC、PD B．是PA
C．可能是PA，也可能是PC、PD D．既是PA，也是PC
二、填空题（每题4分，共16分）
13．
系数为
.
| |
的四位同学的考试成绩
，
且满足
，则这四位同学的考试成绩的所有可能情况的种数为
.
15．已知函数
在区间
上是增函数，则实数
的取值范围是
.
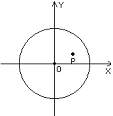
16．P是椭圆
上任意一点，F1、F2是它的两焦点，O为坐标原点，
，则动点Q的轨迹方程是
.
三、解答题
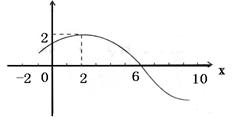
17．（本题12分）已知函数
的图象如图所示.
（Ⅰ）求函数f (x)的解析式；
|
18．（本小题满分12分）
一个口袋中装有大小相同的2个白球和3个黑球.
（1）从中摸出两个球，求两球恰好颜色不同的概率；
（2）从中摸出一个球，放回后再摸出一个球，求两球恰好颜色不同的概率.
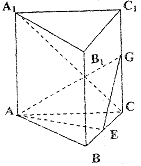
19．（本题12分）
|
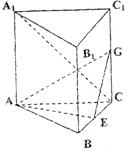
（1）求异面直线AE与A1C所成的角；
（2）求点C1到平面AEG的距离；
（3）求二面角A1—AG—E的大小.
20．（本小题满分12分）已知函数f(x)=x3+ax2+bx+c当x=-1时，取得极大值7，当x=3时，取得极小值，a、b、c的值及其极小值.
21．（12分）已知数列{an}的前n项和为Sn，且满足
.
（1）求证：{
}是等差数列；
（2）求an的表达式；
（3）若bn=2(1－n)·an(n≥2)时，求证：b22+b32+…+bn2＜1.
22．（本小题满分13分）
已知焦点在x轴上的双曲线C的两条渐近线过坐标原点，且两条渐近线与以点
为圆心，1为半径的圆相切，又知C的一个焦点与A关于直线y=x对称.
（Ⅰ）求双曲线C的方程；
（Ⅱ）若Q是双曲线C上的任一点，
为双曲线C的左、右两个焦点，从
引
的平分线的垂线，垂足为N，试求点N的轨迹方程.
参考答案
一、择题：CDBBA CADBB AB
二、填空题：13. 20
14. 15 15. 
16.
三、
17．（Ⅰ）由图象可知，
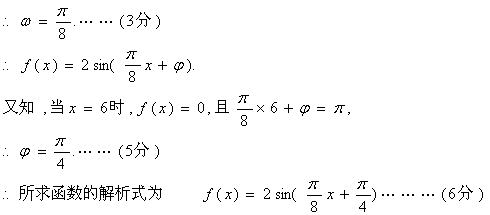
（Ⅱ）
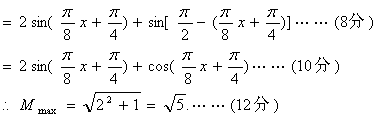
18．（1）记“摸出两个球，两球恰好颜色不同”为A，摸出两个球共有方法C
=10种，其
中，两球一白一黑有C
·C
=6种，…………………………3分
P（A）=
=
…………………………6分
（2）记摸出一球，放回后再摸出一个球“两球恰好颜色不同”为B，摸出一球得白球的概率为
=0.4,
摸出一球得黑球的概率为=0.6，
“有放回摸两次，颜色不同”指“先白再黑”或“先黑再白”，
∴P（B）=0.4×0.6+0.6×0.4=0.48 …………………………12 分
19．解：（1）以点A为坐标原点，分别以AB、AC、AA1为x轴，y轴，z轴建立坐标系
设AC=AB=A1A=2a，则有E（
）A1（
），C（
）,
…………………………2分
|
所以异面直线AE与A1C所成的角是
（4分）
（2）因为G是CC1的中点，所以点C1到平面AEG的距离
与点C到平面AEG的距离相等.
过C做EG的垂线，垂足为H，因为
，
所以CH
，所以
，
所以CH就是点C到平面AEG的距离相等.所以CH=
……………………8分
（3）连AG，设P是AC中点，过P作PQ⊥AG，Q是垂足，连EP、EQ.
又三棱柱是直三棱柱，
平面ACC1A1
∴PQ即为EQ在平面ACC1A1上的射影. 又PQ⊥AG， ∴EQ⊥AG，
∴∠PQE为二面角C—AG—E的平面角. （10分）
同（1）有：PE=a， AP=a ，PQ=
即二面角C—AG—E的平面角是
.
∴二面角A1—AG—E的平面角是
. ………………………… 12分
20．解：∵
∴
依题意有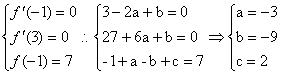
…………………………6分
由
有:－1<x<3
∴f(x)在(-∞,-1)递增，(-1，3)递减，(3，+∞)递增
故f(x)在x=-1取得极大值，在x=3取得极大值，在x=3取得极小值，且
f(x)极小值=f(3)=-25.………………12分
21．（1）证明：
……1分
…………………………………………………… 2分
又
是以2为首项，2为公差的等差数列……4分
（2）解：由（1）
……5分 当n≥2时，
（或n≥2时，
）
当n=1时，
………………7分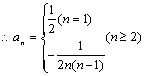 
………………8分
（3）由（2）知，
……………………………9分
…………………10分
…………11分 
………………………12分
22．解：（Ⅰ）设双曲线C的渐近线方程为y=kx，即kx－y=0.
∵该直线与圆
相切，
∴双曲线C的两条渐近线方程为y=±x. ……………………………………………3分
故设双曲线C的方程为
. 又双曲线C的一个焦点为
∴
.∴双曲线C的方程为
.………………………………7分
（Ⅱ）若Q在双曲线的右支上，则延长
到T，使
，
若Q在双曲线的左支上，则在上取一点T，使.
根据双曲线的定义
，所以点T在以
为圆心，2为半径的圆上，即点T的轨迹方程是
① ……………………………………………………10分
由于点N是线段
的中点，设
.
则
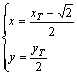即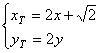
代入①并整理得点N的轨迹方程为
………………………13分