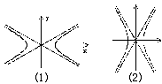高三年级阶段测试数学理

厦门双十中学2007届高三年级阶段测试

数学试题（理）

1．复数等于　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　　B．　　　　　　　　　　 C．　　　　　　　 D．

2．定义集合运算：A⊙B=｛z z= xy(x+y)，x∈A，y∈B｝，设集合A=｛0，1｝，B=｛2，3｝，则集合A⊙B的所有元素之和为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．0　　　 　　　　　　B．6　　　　　 　　 C．12　　　　　　　　　　　D．18

3．函数y＝lnx－1(x＞0)的反函数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．y＝e^x-1(x∈R) 　　 B．y＝e^x+1(x∈R) 　　 C．y＝e^x＋1(x＞1) 　　D．y＝e^x－1(x＞1)

4．已知函数，则下列关于函数性质判断正确的是　　　　（　　）

　　　 A．最小正周期为，一个对称中心是　　 　

　　　 B．最小正周期为，一个对称中心是

　　　 C．最小正周期为，一个对称中心是　　 

　　　 D．最小正周期为，一个对称中心是

5．已知a,b,c为三条不同的直线，且a平面M，b平面N，M∩N=c

①若a与b是异面直线，则c至少与a，b中的一条相交；　　　

②若a不垂直于c，则a与b一定不垂直.

　　　 ③若a//b，则必有a//c；　　　　　　　　　　　　　

　　　 ④若a⊥b，a⊥c则必有M⊥N

　　以上的命题中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．②③④　　　　　　　 B．①③　　　　　　　　　 C．①④　　　　　　　　　 D．②③

6．用1个1，2个2，3个3这6个数可以组成多少个不同的6位数　　　　　　　　　　　　（　　）

　　　 A．20个　　　　　　　 B．60个 　　　　　　　C．120个　　　　　　 D．90个

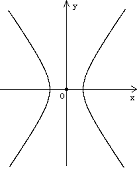
7．已知双曲线的两条渐近线的夹角为（双曲线在角内），则双曲线的离心率为　　　　　　　　　　　　　（　　）

　　　 A．2　　　　　　　　　B．　　 　　　　　 C．　　　 　　 D．

8．已知实数的最小值是　　　　　 （　　）

　　　 A．1　　　　　　　　　　　　B．4　　　　　　　　　　　　C．－4　　　　　　　　　　 D．－1

9．满足函数是奇函数，且在R上是增函数的条件是　　（　　）

　　　 A．p>0 ,q=0　　 　　B．p<0 ,q=0　　 　　C．p≤0，q＝0　 　　 D．p≥0，q=0

10．已知函数在区间上至少取得2个最大值，则正整数t的最小值是（　　）

　　　 A．9　 　　　　　　　　　 B．10　　 　　　　　　　C．11　　 　　　　　　　D．12

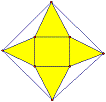
11．有一个正四棱锥，它的底面边长与侧棱长均为a，现用一张正方形包装纸将其完全包住（不能裁剪纸，但可以折叠），那么包装纸的最小边长应为　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

A．　　　　B．　　　C．　　 　 D．

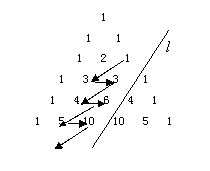
12．如图，在杨辉三角形中，斜线的上方，从1开始箭头所示

的数组成一个锯齿形数列：1,3,3,4,6,5,10,…，记其前n项和

为S_n，则S₁₉等于　　　　　　　　　　　　　　 （　　）

　　　 A．129　　　　　　　　　　 B．172　　　　　

　　　 C．228　　　　  　 D．283

二、填空题（每题4分，共16分）

13．函数f(x)=ax³+bx²+cx+d的部分数值如下:

x	－3	－2	－1	0	1	2	3	4	5	6
y	－80	－24	0	4	0	0	16	60	144	296

则函数y=lgf(x)的定义域为___________.

14．设常数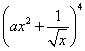，展开式中的系数为，则_____.

15．设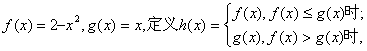函数则函数的最大值是　　　　　 .

16．如图，O是半径为l的球心，点A、B、C在球面上， OA、

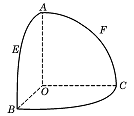
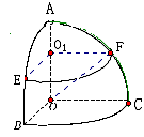
OB、OC两两垂直，E、F分别是大圆弧AB与AC的中点，

则点E、F在该球面上的球面距离是　　　　　　　 

三、解答题

17．（本题12分）

已知A、B、C是三内角，向量，且

　 （1）求角A；（2）若.

18．（本题12分）

某安全生产监督部门对5家小型煤矿进行安全检查(简称安检). 若安检不合格，则必须整改.若整改后经复查仍不合格，则强制关闭. 设每家煤矿安检是否合格是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率是0.8，计算(结果精确到0.01)：

　 （1）恰好有两家煤矿必须整改的概率；（2）某煤矿不被关闭的概率；（3）至少关闭一家煤矿的概率.

19．（本题12分）

已知a₁=2，点(a_n,a_n+1)在函数f(x)=x²+2x的图象上，其中=1，2，3，…

　 （1）证明数列｛lg(1+a_n)｝是等比数列；

　 （2）设T_n=(1+a₁) (1+a₂) …(1+a_n)，求数列｛a_n｝的通项及T_n；

20．（本题12分）

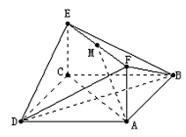
如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=，AF=1，M是线段EF的中点.

　 （1）求证AM∥平面BDE；

　 （2）求二面角A—DF—B的大小；

　 （3）试在线段AC上确定一点P，使得PF与BC所成角是60⁰.

21．（本题12分）

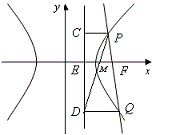
已知双曲线C：（>0,>0）的离心率为，右焦点为F,过点G（1,0）且斜率为1的直线与双曲线C交于A、B两点，并且。

　 （1）求双曲线方程C；

　 （2）过（1）中双曲线C的右焦点F，引直线交双曲线右支于P、Q两点，设P、Q两点在双曲线右准线的射影分别为点C、D，右准线与轴交于E点，线段EF的中点为M，求证： P、M、D三点共线。

22．（本题14分）

已知函数.

　 （1）求函数在区间上的最大值；

　 （2）求证：在区间上，函数的图象在函数的图象的下方；

　 （3）设，求证：.

参考答案

一、选择题：ADBAB　BDCDC　AD　　　　　　 

二、填空题：(－1,1)和(2,+∞)；　 1；　 1；　　

1．解：=

2．解：①x=0时，z=0；②x=1，y=2时z=6；　 x=1,y=3时z=12　　 所有元素之和为18.

3．解：y的值域为R，反函数为y＝e^x+1(x∈R)

4．解：=，T=，再将代入满足.

注：三角函数的对称中心位于“图象的平衡位置上”即将x=　　　　代入后

三角函数的对称轴位于“图象的最值处”即将x=　　　　代入后

5．④两直线必须相交.

6．解1：；解2：先从6个位置中选择3个位置让“3”站，再从剩下的3个位置中选2个位置给“2”站，剩下的位置给“1”站.则

7．解：①

②假如本题将“双曲线在角内”去掉，

则还可以出现第二种情况.9

8．解：依题意可知点P(x,y)在直线4x+3y=0上运动，求的最小值

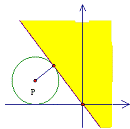
先求点(-2,1)到P(x,y)的距离-----------

的最小值=

9．解：f(x)为奇函数，则f(0)=0，所以q=0；

当时，，则作图可知时，f(x)为增函数.

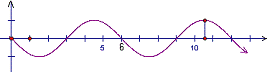
10．解：函数的周期为6，依题意可知

，所以正整数t的最小值为11.

11．解：将正四棱锥展开得图，当正方形如图放置时，

所需正方体的边长最小，不难求得A.

12．提示：第一行C₂²，第二行C₃¹+C₃²=C₄²，

第三行C₄¹+C₄²=C₅²，…，

故S₁₉=C₂²+C₄²+C₅²+…+C₁₂²=C₁₃³-C₃²=283.

13．解：由f(x)的解析式可知f(x)图象连续及f(x)的单调性可确定,

在(－1,1)和(2,+∞)上均有f(x)＞0.

14．解：，由，所以

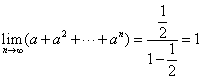，所以为1.

15．解：依题意可作出图形（如右所示）可知在（1，1）处取最值.

16．解：本题关键是求球心角

在面AOC中，F为中点，所以，得

同理得，在中EF=1，所以在中，所以EF两点的球面距离=

17．解：（1）∵ ∴　

即,　

∵　∴　

∴----------------6分

　 （1）由题知，

------------10分

所以 ∴

-------------------------------------12分

18．解：（1）记恰好有两家煤矿必须整改为事件A；

所以.

　 （2）解法一（对立事件）记该煤矿不被关闭为事件B；.

解法二　（分类穷举）记该煤矿不被关闭为事件B；所以.

　 （3）记至少关闭一家煤矿为事件C.所以.

19．解：（1）由已知，　　

，，两边取对数得，即

是公比为2的等比数列.-----------------------------------------------------------6分

　 （2）由（1）知

------------------- 8分

　　　 　　　 =--------12分

20．解1：（1）记AC与BD的交点为O,连接OE,∵O、M分别是AC、EF的中点，ACEF是矩形，

∴四边形AOEM是平行四边形，∴AM∥OE.∵平面BDE， 平面BDE，

∴AM∥平面BDE.

　 （2）在平面AFD中过A作AS⊥DF于S，连结BS，

∵AB⊥AF， AB⊥AD，

∴AB⊥平面ADF，

∴AS是BS在平面ADF上的射影，由三垂线定理得BS⊥DF.

∴∠BSA是二面角A—DF—B的平面角.

在RtΔASB中，∴

∴二面角A—DF—B的大小为60º.

　 （3）设CP=t（0≤t≤2）,作PQ⊥AB于Q，则PQ∥AD，

∵PQ⊥AB，PQ⊥AF，，∴PQ⊥平面ABF，

平面ABF，

∴PQ⊥QF.在RtΔPQF中，∠FPQ=60º，PF=2PQ.

∵ΔPAQ为等腰直角三角形，

∴又∵ΔPAF为直角三角形，∴，

∴所以t=1或t=3(舍去)即点P是AC的中点.

解2：（1）建立如图所示的空间直角坐标系.设，连接NE，

则点N、E的坐标分别是（、（0,0,1）,

 ∴=(,

又点A、M的坐标分别是（）、（

∴=（

∴，NE=AM且NE与AM不共线，∴NE∥AM.

又∵平面BDE， 平面BDE，∴AM∥平面BDF.

　 （Ⅱ）∵AF⊥AB，AB⊥AD，AF∴AB⊥平面ADF.

∴为平面DAF的法向量.

∵=（·=0，

∴=（·=0，　　

∴为平面BDF的法向量.

∴cos<>=，的夹角是60º.即所求二面角A—DF—B的大小是60º.

　 （Ⅲ）设P(t,t,0)(0≤t≤)得∴=（，0，0）

又∵PF和CD所成的角是60º.∴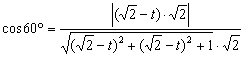

解得或（舍去），

即点P是AC的中点.

21．解：（1）由已知：　所以双曲线方程为-------------1分

直线AB方程为：，代入得：　--------2分

--------3分

　--------5分

　 -------6分

　 （2）法一：可得焦点F(3,，0),M（2，0）.故设直线为，代入得

，设P()，Q()

则--------8分

要证P,M,D三点共线，只须证,即可

，

＝即--------10分

又

P,M,D三点共线　　　　  --------12分

　 （法二）连接PD，设PD与x轴交于点N, 则,

又,--------5分

,,，--------10分

,N是线段EF的中点，所以N，M,重合， P,M,D三点共线--------12分

22．解：（1）∵，当时，．……………2分

　　　 ∴在区间上为增函数，∴．　　  ……………4分

　 （2）令，　　　 则．……………6分

　　　 当时，．∴在区间上为减函数．

　　　 又函数在处连续，且． ∴，

即.

　　　 在区间上，函数的图象在函数的图象的下方．…………9分

　 （3）证法一：，

当时，不等式成立．

当时，

　　　 ∴．………………………………………………………14分

证法二：数学归纳法①当时，不等式成立．

当时，左边，右边，不等式成立．

②假设当时，不等式成立，即．

那么，当时，

　　　

　　　 这就是说，当时，不等式也成立．　 由（1）（2）知，对于一切正整数ｎ不等式都成立.