高三数学第一学期期末五校联考
数学科(文科)试题
本试卷分选择题和非选择题两部分,共4页,满分为150分,考试时间120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号填写在答题卡上。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案;不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
第一部分 选择题(共50分)
一、选择题(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.设I是全集,I={0,1,2,3,4},集合A={0,l,2,3},集合B={4},则![]()
( )
A.{0} B.{0,1} C.{0,1,2,3,4} D.{0,1,4}
2.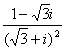 =
( )
=
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 已知函数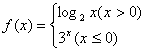 ,则
,则![]() 的值是
( )
的值是
( )
A.9 B.![]() C.-9
D.-
C.-9
D.-![]()
4.设![]() 且
且![]() ,则锐角x为
( )
,则锐角x为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
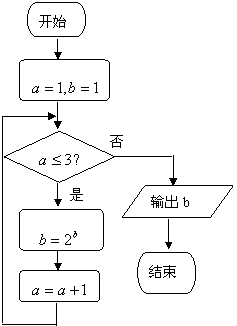 5.如图,该程序运行后输出的结果为 ( )
5.如图,该程序运行后输出的结果为 ( )
A.1 B.2
C.4 D.16
![]() 6.不等式组
6.不等式组![]() 所表示的平面
所表示的平面
区域是 ( )
A.一个三角形
B.一个梯形
C.直角三角形
D.两个等腰直角三角形
7.设下表是某班学生在一次数学考试中数学成绩的分布表
| 分数段 |
|
|
|
|
|
|
| 人 数 | 7 | 6 | 8 | 12 | 6 | 6 |
那么分数在![]() 中的频率和分数不满110分的累积频率约分别是 ( )
中的频率和分数不满110分的累积频率约分别是 ( )
A.0.18, 0.47 B.0.47, 0.18 C.0.18, 1 D.0.38, 1
8.已知等比数列![]() 的首项为8,
的首项为8,![]() 是其前
是其前![]() 项的和,某同学经计算得
项的和,某同学经计算得![]() =8,
=8,![]() =20,
=20,![]() =36,
=36,![]() =65,后来该同学发现其中一个数算错了,则该数为
( )
=65,后来该同学发现其中一个数算错了,则该数为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.定义两种运算:![]() a
a![]() b=
b=![]() ,则函数f(x)=
,则函数f(x)=![]() 为( )
为( )
A.奇函数 B.偶函数
C.奇函数且为偶函数 D.非奇函数且非偶函数
第二部分 非选择题(共100分)
 二、填空题:(每小题5分,共20分,其中14小题为选做题,考生从给出的两题中选择其中一道作答,若两题全答的只计算前一题得分。)
二、填空题:(每小题5分,共20分,其中14小题为选做题,考生从给出的两题中选择其中一道作答,若两题全答的只计算前一题得分。)
11.函数![]() 的定义域为_____________
的定义域为_____________
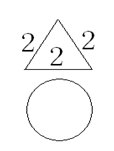
12.一个几何体的正视图和侧视图均是边长为2的正三角形,俯视
图为一个圆,如右图,这个几何体的体积为
13.对2×2数表定义平方运算如下:
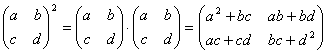 ,则
,则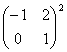 =__________.
=__________.
14.▲选做题:在下面两道题中选做一题,两道题都选的只计算前一题的得分。
 (1)过点
(1)过点![]() 的直线的参数方程
的直线的参数方程![]() ,若此直线与直线
,若此直线与直线![]() 相交于点B,则|AB|=
相交于点B,则|AB|=
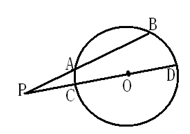
(2)如右图,已知⊙O的割线PAB交⊙O于A,B两点,割线PCD经过圆心,若PA=3,AB=4,PO=5,则⊙O的半径为_______________
三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤)
15.(本题满分12分)某射手进行射击训练,假设每次射击击中目标的概率为![]() ,且各次射击的结果互不影响.
,且各次射击的结果互不影响.
(1)求射手在3次射击中,3次都击中目标的概率(用数字作答);
(2)求射手在3次射击中,恰有两次连续击中目标的概率(用数字作答);
(3)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答).
16.(本小题满分12分)在⊿ABC中,角A、B、C所对的边分别为a、b、c,且![]()
(1)求tanC的值; (2)若⊿ABC最长的边为1,求b。
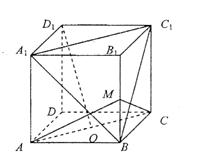
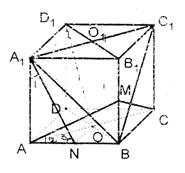
|
(1)D1O//平面A1BC1;
(2)D1O⊥平面MAC.
18.(本小题满分14分)已知数列![]() 的前
的前![]() 项和
项和![]() .
.
(1) 求数列{![]() }的通项公式;
}的通项公式;
(2)设![]() ,求数列{
,求数列{![]() }的前
}的前![]() 项和.
项和.
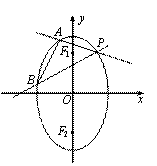
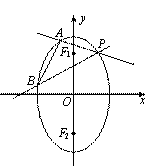 19.(本小题满分14分)已知椭圆
19.(本小题满分14分)已知椭圆![]() 两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足
两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足![]() ,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
(1)求P点坐标;
(2)求证直线AB的斜率为定值;
(3)求△PAB面积的最大值。
20.(本小题满分14分)设M是由满足下列条件的函数![]() 构成的集合:“①方程
构成的集合:“①方程![]() 有实数根;②函数
有实数根;②函数![]() 的导数
的导数![]() 满足
满足![]() .”
.”
(1)判断函数![]() 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
(2)集合M中的元素![]() 具有下面的性质:若
具有下面的性质:若![]() 的定义域为D,则对于任意
的定义域为D,则对于任意![]() ,都存在
,都存在![]() ,使得等式
,使得等式![]() 成立”,试用这一性质证明:方程
成立”,试用这一性质证明:方程![]() 只有一个实数根;
只有一个实数根;
(3)设![]() 是方程
是方程![]() 的实数根,求证:对于
的实数根,求证:对于![]() 定义域中任意的
定义域中任意的![]() ,当
,当![]() ,且
,且![]() 时,
时,![]() .
.
高三数学第一学期期末五校联考
数学科(文科)答案
一、CBBBD DACCA
二、11、由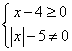 解得
解得![]() ,所以函数
,所以函数![]() 的定义域为{x
的定义域为{x![]() }
}
12.三视图知这个几何体为圆锥,它的体积为
![]()
13.![]()
14.(1)由![]()
得点 ![]()
(2)提示:设圆的半径为R,由![]() 得
得![]() 解得R=2
解得R=2
三、15.解: (1)记事件“射手在3次射击中,3次都击中目标”为事件A,
![]() ;………………………………………4分
;………………………………………4分
(2)记事件“射手在3次射击中,恰有两次连续击中目标”为事件B,
![]() ;………………………………………8分
;………………………………………8分
(3)记事件“射手第3次击中目标时,恰好射击了4次”为事件C,
![]() ………………………………………12分
………………………………………12分
16.解:(1)![]()
![]() B为锐角,且
B为锐角,且![]() ,
,![]() ,………………3分
,………………3分
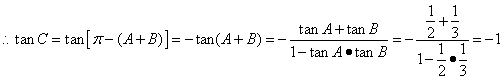 ………………6分
………………6分
(2)由(1)知C为钝角,所以C是最大角,所以最大边为c=1, ………………8分
![]() , ………………10分
, ………………10分
由正弦定理:![]() 得
得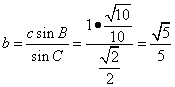 。 ………………12分
。 ………………12分
17.证明:证明: (1)连结![]() 分别交
分别交![]() 于
于![]() ………………1分
………………1分
|
![]() 分别是
分别是![]() 的中点
的中点
![]() ………………3分
………………3分
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
![]() ………………5分
………………5分
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ………………7分
………………7分
(2)连结![]() ,设正方体
,设正方体![]() 的棱长为
的棱长为![]() ,
,
在正方体![]() 中,对角面
中,对角面![]() 为矩形且
为矩形且![]() ………………8分
………………8分
![]() 分别是
分别是![]() 的中点
的中点
![]()
![]() ………………10分
………………10分
![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]() ,即
,即![]()
说明:(也可以计算![]() 三边长度,验证
三边长度,验证![]() ,从而得
,从而得![]() )
)
在正方体![]() 中
中
![]() 平面
平面![]()
![]()
又![]() ,
,![]()
![]() 平面
平面![]() ………………12分
………………12分
![]() 平面
平面![]()
![]()
又![]()
![]() 平面
平面![]() ………………14分
………………14分
另证:过O作ON//BC交AB于N………………8分

……………11分

………………14分
18.解:(1)![]() 时,
时,![]() ;
………………2分
;
………………2分
当![]() . ………………4分
. ………………4分
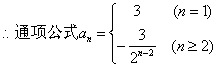 ………………6分
………………6分
(2) 设{![]() }的前
}的前![]() 项和为
项和为![]() ,当
,当![]() 时,
时,
![]() ;………………8分
;………………8分
![]() 时,
时,![]() ,
,![]()
![]()
![]() ………………10分
………………10分
![]()
![]()
![]()
![]() =
=![]()
![]() ………………14分
………………14分
19.解:(1)由题可得![]() ,
,![]() ,设
,设![]()
则![]() ,
,![]() ,……………………2分
,……………………2分
∴![]() ,∵点
,∵点![]() 在曲线上,则
在曲线上,则![]() ,∴
,∴![]() ,从而
,从而![]() ,得
,得![]() .则点P的坐标为
.则点P的坐标为![]() . ……………………5分
. ……………………5分
(2)由题意知,两直线PA、PB的斜率必存在,设PB的斜率为![]() ,………6分
,………6分
则BP的直线方程为:![]() .由
.由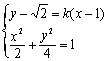 得
得![]()
![]() ,设
,设![]() ,则
,则![]() ,
,
 同理可得
同理可得![]() ,则
,则![]() ,
,![]() . ………………9分
. ………………9分
所以:AB的斜率![]() 为定值. ………………10分
为定值. ………………10分
(3)设AB的直线方程:![]() .
.
由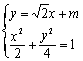 ,得
,得![]() ,
,
由![]() ,得
,得![]()
P到AB的距离为![]() ,………………12分
,………………12分
则![]()
![]() 。
。
当且仅当![]() 取等号
取等号
∴三角形PAB面积的最大值为![]() 。………………14分
。………………14分
20.解:(1)因为![]() ,所以
,所以![]() 满足条件
满足条件![]() ,………2分
,………2分
又因为当![]() 时,
时,![]() ,所以方程
,所以方程![]() 有实数根0.
有实数根0.
所以函数![]() 是集合M中的元素. ………………………………………………5分
是集合M中的元素. ………………………………………………5分
(2)假设方程![]() 存在两个实数根
存在两个实数根![]() ),则
),则![]() ,不妨设
,不妨设![]() ,根据题意存在数
,根据题意存在数![]() ,
,
使得等式![]() 成立, ……………………………………………7分
成立, ……………………………………………7分
因为![]() ,
,![]() ,且
,且![]() ,所以
,所以![]() ,
,
与已知![]() 矛盾,所以方程
矛盾,所以方程![]() 只有一个实数根;…………………10分
只有一个实数根;…………………10分
(3)不妨设![]() ,因为
,因为![]() 所以
所以![]() 为增函数,所以
为增函数,所以![]() ,
,
又因为![]() ,所以函数
,所以函数![]() 为减函数,
为减函数,
所以![]() ,
,
所以![]() ,即
,即![]() ,………………………12分
,………………………12分
所以![]()
![]() .…………………………………………14分
.…………………………………………14分