高三数学第一学期期末抽查试卷
一、填空题：
1、 集合
，若
，则
。
2、 设函数
，则
的值为 
。
3、 设等差数列
的公差为2，且
，则
。
4、 不等式
的解为 
。
5、 已知
，则
的值为 
。
6、 2005年1月6日是“中国十三亿人口日”，如果要使我国总人口在2015年以前控制在十四亿之内，那么从2005年1月6日开始的随后10年中我国的年平均人口自然增长率应控制在 
%以内（精确到0.01）。
7、 若函数
是奇函数，且周期为
，则
（写出一个你认为符合题意的函数即可）。
8、 一个布袋中共有10个除了颜色之外完全相同的球，其中4个白球，6个黑球，则一次任意摸出两球中至少有一个白球的概率为 
。
9、 方程
的正实数根
（结果精确到0.1）。
10、考察下列一组不等式：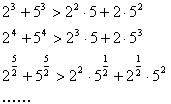
将上述不等式在左右两端仍为两项和的情况下加以推广，使以上的不等式成为推广不等式的特例，则推广的不等式为
。
二、选择题：
11、设
、
，则
是
的
（ D ）
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不是充分条件，也不是必要条件
12、若
，则
的值为
（ A ）
A、2
B、
C、1
D、
13、若等比数列对一切正整数
都有
，其中
是的前项的和，则公比
的值为（ C ）
A、
B、
C、2
D、
14、函数
在区间
上存在
，使
，则的取值范围是
（ C ）
A、
B、
C、
D、
三、解答题：
15、设
为奇函数，且当
时，
（Ⅰ）求当
时，的解析表达式；
（Ⅱ）解不等式
。
解：（Ⅰ）时，
。
（Ⅱ）由题意，得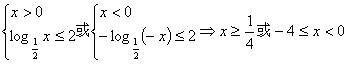
。
16、已知函数
，
（Ⅰ）求函数的最小正周期，并写出其所有单调递减区间；
（Ⅱ）若
，求函数的最大值
与最小值
。
解：（Ⅰ）
，单调递减区间：
（Ⅱ）
。
17、现定义复函数如下：在某个变化过程中有两个变量
与
，如果对于的某个范围D内的每一个确定的复数，按照某个对应法则
都有唯一确定的复数与它对应，那么，我们就称是的复函数，记作
。
设复函数
，
（Ⅰ）求
的值； （Ⅱ）若
，求的值。
解：（Ⅰ）
。
（Ⅱ）设
，
，
∴
。
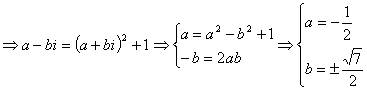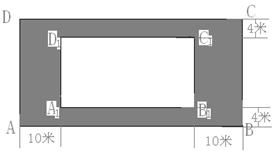
18、某房地产开发公司计划在一楼区内建造一个长方形公园
，公园由长方形的休闲区
和环公园人行道（阴影部分）组成。已知休闲区的面积为
平方米，人行道的宽分别为
米和米（如图）
（Ⅰ）若设休闲区的长和宽的比
，求公园所占面积
关于
的函数
的解析式；
（Ⅱ）要使公园所占面积最小，休闲区的长和宽该如何设计？
解：（Ⅰ）设休闲区的宽为米，则其长为
米，
∴
，
∴
（Ⅱ）
，当且仅当
时，公园所占面积最小，
此时，
，即休闲区的长为
米，宽为
米。
19、已知一列向量
，满足
，
（Ⅰ）证明：
是等比数列；
（Ⅱ）求向量
与
的夹角
；
（Ⅲ）把中所有与
共线的向量按原来的顺序排成一列，记为
，令
，
为坐标原点，求点列
的极限点
的坐标。（注：若点
坐标为
，且
，则称点
为点列的极限点。）
解：（Ⅰ）
，
，
，
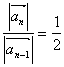是首项为
，公比为的等比数列。
（Ⅱ）∵
，
∴向量与的夹角
。
（Ⅲ）由（Ⅱ）可知，∥
∥
∥…，即
，∴
，
设，则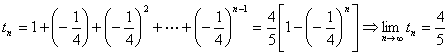
，
，
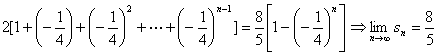∴点列的极限点的坐标为
。
20、已知集合是满足下列性质的函数的全体：在定义域内存在，使得
成立。
（Ⅰ）函数
是否属于集合？说明理由；
（Ⅱ）设函数
，求的取值范围；
（Ⅲ）设函数
图象与函数
的图象有交点，证明：函数
。
解：（Ⅰ）若
，在定义域内存在，则
，
∵方程
无解，∴
。
（Ⅱ）
，
时，
；
时，由
，得
。
∴
。
（Ⅲ）∵
，
又∵函数图象与函数的图象有交点，设交点的横坐标为，
则
，其中
。
∴，即。