高三数学第一学期期末考试卷
一、填空题（本大题共12小题，每小题4分，满分48分）
1．
。
2．函数
的定义域为 。
3．不等式
的解为 。
4．已知
，则
。
5．计算：
。
6．函数
的反函数经过点（2，3），则b= 。
7．数列{an}中，若a1=1，an-1an=n（n≥2），则a4= 。
8．（理）在极坐标系中，O是极点，
，
则△AOB的形状为 。
（文）某工程由下列工序组成，则工程总时数为 天。
| 工 序 | a | b | c | d | e | f |
| 紧前工序 | - | a | b | c | c | d,e |
| 工时数(天) | 2 | 2 | 4 | 5 | 4 | 3 |
9．有4条线段，长度分别为3、5、7、8，从这4条线段中任取3条，则所取3条线段能
构成三角形的概率是 。
10．在Rt△ABC中，
，
，则边c长为 。
11．方程
的解的个数是 。
12．有穷数列{an}，Sn为其前n项和，定义
为数列{an}的“凯森和”，
如果有99项的数列a1、a2、a3、…、a99的“凯森和”为1000，则有100项的数列
1、a1、a2、a3、a4、…a99的“凯森和”
= 。
二、选择题（本大题共4题，每小题4，满分共16分）
13．“
”是“
”的（ ）
（A）充分非必要条件； （B）必要非充分条件；
（C）充要条件； （D）既非充分又非必要条件。
14．复数z1=2+i，z2=1-i，则z1×z2在复平面内的对应点位于 （ ）
（A）第一象限； （B）第二象限；
（C）第三象限； （D）第四象限；
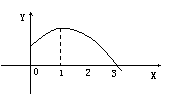15．函数
的部分图象如图，则
、
可以取的一组值是 （ ）
（A）
；
（B）
；
（C）
；
（D）
；
16．已知：命题p：函数
的值域为R；
命题q：函数
是减函数；
若p或q为真命题，p且q为假命题，则实数a的取值范围为 （ ）
（A）a≤1； （B）a＜2；
（C）1＜a＜2； （D）a≤1或a≥2 。
三、解答题（本大题共4小题，满分86分）
17．（本题满分12分）关于x的方程
有一实根为n，设复数
，求m、n的值及复数z的值。
解：
18．（本题满分12分）
已知集合
，
，
求
解：
19．（本题满分14分）
先阅读下列不等式的证法，再解决后面的问题：
已知
，
，求证
，
证明：构造函数
因为对一切xÎR，恒有
≥0，所以
≤0,
从而得，
（1）若
，
，请写出上述结论的推广式；
（2）参考上述解法，对你推广的结论加以证明。
解：
20．（本题满分14分）
现有一批货物用轮船从上海洋山深水港运往青岛，已知该船航行的最大速度为35海
里/小时，上海至青岛的航行距离约为500海里，每小时运输成本由燃料费用和其余
费用组成。轮船每小时的燃料费用与轮船速度的平方成正比（比例系数为0.6），其
余费用每小时960元。
（1）把全程运输y（元）表示为速度x（海里/小时）的函数；
（2）为了使全程运输成本最小，轮船应以多大速度行驶？
解：
21．（本题满分16分）
已知在数列
中，
，
，
(
、
Î
,¹0)。
（1）若=2，=-1，求
、
，并猜测
；
（2）[理]若
是等比数列，且
是等比数列，求、满足的条件；
[文]¹1，若是等比数列，且是等比数列，求、满足的条件；
（3）一个质点从原点出发，依次按向右、向上、向左、向下的方向交替地运动，第
次
运动的位移是
，质点到达点
。设点
的横坐标为
，若=0，若
，
求。
解：
22．（本题满分18分）
已知函数
，
，
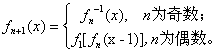
（1）若函数
，求函数
、
的解析式；
（2）[理]若函数
，函数
的定义域是[1,2]，
求
的值；
[文]若函数，求函数的定义域；
（3）设是定义在上的周期为4的奇函数，且函数的图像关于直线
对称。当
时，
，求正数的最小值及函数在[-2,2]上
的解析式。
解：
高三数学第一学期期末考试卷解答
一、填空题（本大题共12小题，每小题4分，满分48分）
1． 2p/3 。
2．函数的定义域为 (-1,1) 。
3．不等式的解为 x＜0或x＞1 。
4．已知，则 
。
5．计算： 1 。
6．函数的反函数经过点（2，3），则b= -6 。
7．数列{an}中，若a1=1，an-1an=n（n≥2），则a4= 8/3 。
8．（理）在极坐标系中，O是极点，，则△AOB的形状为 等腰直
角三角形 。
（文）某工程由下列工序组成，则工程总时数为 16 天。
| 工 序 | a | b | c | d | e | f |
| 紧前工序 | - | a | b | c | c | d,e |
| 工时数(天) | 2 | 2 | 4 | 5 | 4 | 3 |
9．有4条线段，长度分别为3、5、7、8，从这4条线段中任取3条，则所取3条线段能
构成三角形的概率是 3/4 。
10．在Rt△ABC中，，，则边c长为 
。
11．方程的解的个数是 7 。
12．有穷数列{an}，Sn为其前n项和，定义为数列{an}的“凯森和”，
如果有99项的数列a1、a2、a3、…、a99的“凯森和”为1000，则有100项的数列
1、a1、a2、a3、a4、…a99的“凯森和”= 991 。
二、选择题（本大题共4题，每小题4，满分共16分）
13．“”是“”的 （ B ）
（A）充分非必要条件； （B）必要非充分条件；
（C）充要条件； （D）既非充分又非必要条件。
14．复数z1=2+i，z2=1-i，则z1×z2在复平面内的对应点位于 （ D ）
（A）第一象限； （B）第二象限；
（C）第三象限； （D）第四象限；
15．函数的部分图象如图，则、可以取的一组值是 （ C
）
（A）；
（B）；
（C）；
（D）；
16．已知：命题p：函数的值域为R；
命题q：函数是减函数；
若p或q为真命题，p且q为假命题，则实数a的取值范围为 （ C ）
（A）a≤1； （B）a＜2； （C）1＜a＜2； （D）a≤1或a≥2 。
三、解答题（本大题共4小题，满分86分）
17．（本题满分12分）关于x的方程
有一实根为n，设复数
，求m、n的值及复数z的值。
解：∵实数n是方程
的一个根，
∴
, (4¢) 
，∴n=1，m=1, (8¢)
. (12¢)
18．（本题满分12分）
已知集合，，
求
解：由
，得
, (2¢) 解得
, (4¢)
, (6¢)
∵0＜x＜
, ∴
＜x+
＜
, ∴
=(1,2] (10¢),
∴=[
]∩(1,2]=(1,
] (12¢)
19．（本题满分14分）
先阅读下列不等式的证法，再解决后面的问题：
已知，，求证，
证明：构造函数
因为对一切xÎR，恒有≥0，所以≤0,
从而得，
（1）若，，请写出上述结论的推广式；
（2）参考上述解法，对你推广的结论加以证明。
解：（1）若
，
，
求证：
(4¢)
（2）证明：构造函数
(6¢)
(9¢)
(11¢)
因为对一切xÎR，都有≥0，所以△=
≤0,
从而证得：
. (14¢)
20．（本题满分14分）
现有一批货物用轮船从上海洋山深水港运往青岛，已知该船航行的最大速度为35海
里/小时，上海至青岛的航行距离约为500海里，每小时运输成本由燃料费用和其余
费用组成。轮船每小时的燃料费用与轮船速度的平方成正比（比例系数为0.6），其
余费用每小时960元。
（1）把全程运输y（元）表示为速度x（海里/小时）的函数；
（2）为了使全程运输成本最小，轮船应以多大速度行驶？
解：设每小时燃料费用为m元，则m=
(0＜x≤35) (2¢)
由题意，全程所用的时间为
小时，所以
，xÎ(0,35] (4¢)
故所求的函数为
，xÎ(0,35] (6¢)
（2）以下讨论函数，xÎ(0,35]的单调性：
设0＜x1＜x2≤35, (7¢)
(10¢)
∵0＜x1＜x2≤35，∴x1-x2＜0，x1x2＞0，x1x2＜1225Þ x1x2-1600＜0，
∴
＞0Þ
(12¢)
∴函数，xÎ(0,35]是减函数，故当轮船速度为35海里/小时时，
所需成本最小. (14¢)
注：未经证明，直接说函数，xÎ(0,35]是减函数而得出结论,扣2分.
21．（本题满分16分）
已知在数列中，，，(、Î,¹0)。
（1）若=2，=-1，求、，并猜测；
（2）[理]若是等比数列，且是等比数列，求、满足的条件；
[文]¹1，若是等比数列，且是等比数列，求、满足的条件；
（3）一个质点从原点出发，依次按向右、向上、向左、向下的方向交替地运动，第次
运动的位移是，质点到达点。设点的横坐标为，若=0，若，
求。
解：（1）∵
， (2¢)
∴猜测: 
. (4¢)
（2）（理）由
，
得
，
当
时，
，显然是等比数列，
当
时，因为，只有
时，才是等比数列
∴Þ
，即
，或 (6¢)
由， 得
(n≥2),
当
时，
(n≥2)，显然
是等差数列，
当
时，
，只有
时，才是等差数列，
，即
，或 (8¢)
综上，、满足的条件是 (10¢)
（文）∵是等比数列，，∴，或 (6¢)
∵是等差数列，
，∴ (8¢)
∴、满足的条件是 (10¢)
（3）∵
，∴
(12¢)
∴
,…,
∴
. (14¢)
∵
，∴
(16¢)
22．（本题满分18分）
已知函数，
，
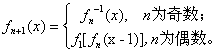
（1）若函数，求函数、的解析式；
（2）[理]若函数，函数的定义域是[1,2]，
求的值；
[文]若函数，求函数的定义域；
（3）设是定义在上的周期为4的奇函数，且函数的图像关于直线
对称。当时，，求正数的最小值及函数在[-2,2]上
的解析式。
解：（1）∵ 
， (1¢) ∴ 
； (2¢)
； (4¢)
. (6¢)
（2）（理）∵ 
，∴
, (7¢)
, (8¢)
， (9¢)
∴
. (11¢)
由题设，得
. (12¢)
（文）∵ ，∴, (7¢)
∴ , (9¢)
, (11¢)
∴ 的定义域为
. (12¢)
（3）∵是定义在R上的奇函数，∴
①
∵函数的图象关于直线
对称，∴
②
在②式中以
替换
，得 
③
由①式和③式，得 
④
在④式中以
替换，得 
⑤
由④式和⑤式，得 
(14¢)
∵是定义在R上的周期为4的奇函数，∴正数的最小值是1. (16¢)
∴当Î[0,1]时，
，∴当Î[-1,0]时，Î[0,1]，
，即
.
∵函数的图象关于直线
对称，
∴当Î(1,2]时，2-Î[0,1)，
当Î[-2,-1)当，Î(1,2]，
，即
.
∴
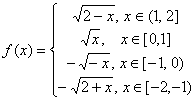. (18¢)