高三数学第一学期期末联考试题
命题人:岳西中学 储炳南 审题人:野寨中学:徐金友
注意事项:
1.本试卷分第Ⅰ卷(试题卷)和第Ⅱ卷(答题卷)两部分,共150分。考试时间120分钟。
2.考生一律不准使用计算器。
第Ⅰ卷
一、选择题(本大题共11小题,每小题5分,共55分;每小题给出的四个选项中,只有一个是符合要求的。)
1.已知向量![]() ,
,![]() ,则
,则![]() 与
与![]() ( )
( )
A.垂直 B.不垂直也不平行 C.平行且同向 D.平行且反向
2.设A={x-1<x<2},B={xx2<a},若B![]() A,则实数a的取值范围是( )
A,则实数a的取值范围是( )
A.a<1 B.a≤1 C.0≤a≤1 D.1≤a≤4
3、下列不等式中解集为实数集R的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
4.若等差数列前n项和为48,前2n项和为60,则前3n项之和为( )
A.84 B.72 C.36 D.-24
5.若![]() ,则
,则![]() 的值为
( )
的值为
( )
A、2 B、![]() C. -2 D.
C. -2 D. ![]()
6.已知![]() ,且方程
,且方程![]() 的解依次成等差数列,则a的值为( )
的解依次成等差数列,则a的值为( )
A.2 B.3 C.4 D.2、3、4
7. 在![]() 的展开式中,任取一项,则取出的是有理项的概率为( )
的展开式中,任取一项,则取出的是有理项的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.下列关于函数![]() 的叙述正确的是( )
的叙述正确的是( )
A.当且仅当x=1时,![]() 取得最小值2
B.当且仅当
取得最小值2
B.当且仅当![]() 时,
时,![]() 取得最小值2
取得最小值2
C.当且仅当![]() 时,
时,![]() 取得最小值2 D.当且仅当
取得最小值2 D.当且仅当![]() 时取得最大值4
时取得最大值4
9. 已知函数![]() 的导数
的导数![]() 处取得极大值,则a的取值范围是 ( )
处取得极大值,则a的取值范围是 ( )
A.(-![]() ,-1) B.(-1,0) C.(0,1) D.(0,+
,-1) B.(-1,0) C.(0,1) D.(0,+![]() )
)
10.已知函数![]() ,若方程
,若方程![]() 的两根分别为
的两根分别为![]() ,若
,若![]() ,则
,则![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
11.已知![]() ,满足
,满足![]() 且
且![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.[0,1] B.(0,1) C.![]() D.
D.![]()
二、填空题(本大题共4小题,每小题4分,共16分)
12.设O是△ABC内部一点,且![]() 的面积之比为
的面积之比为
13. 已知![]() ,则
,则![]() =
=
14.在等比数![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,若数列
,若数列![]() 也是等比数列,则
也是等比数列,则![]() 等于
等于
15.随机变量ξ的分布列为![]() ,k=1、2、3、4,c为常数,则
,k=1、2、3、4,c为常数,则![]() 的值为
的值为
三、解答题(本大题共6小题,共79分)
16.(12分)已知集合![]()
(1)若![]() ,求a的取值范围;(2)若
,求a的取值范围;(2)若![]() ,求
,求![]() 的取值范围。
的取值范围。
17.(12分)设函数![]() ,
,![]() 图像的一条对称轴是直线
图像的一条对称轴是直线![]() .(1)求
.(1)求![]() 值;(2)求函数
值;(2)求函数![]() 的单调递减区间; (3)已知A、B函数
的单调递减区间; (3)已知A、B函数![]() 的图像上任意两点,求直线AB的斜率的取值范围。
的图像上任意两点,求直线AB的斜率的取值范围。
18.(14分)已知函数![]() 在
在![]() 上是增函数。(1)求a的取值范围;(2)求
上是增函数。(1)求a的取值范围;(2)求![]() 的极值;(3)若
的极值;(3)若![]() 有三个不同的实根,求a的取值范围。
有三个不同的实根,求a的取值范围。
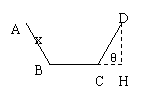 19.(14分)某工程建设中,需用宽为2,长为
19.(14分)某工程建设中,需用宽为2,长为![]() 的矩形铁皮建造大量的长度为
的矩形铁皮建造大量的长度为![]() 的引水槽,按工程设计要求,引水槽过水横断面应设计为等腰梯形,为了使引水槽的过水流量最大,应使引水槽的横断面面积S为最大,如果设引水槽横断面的等腰梯形的腰长为x,腰与下底的夹角为
的引水槽,按工程设计要求,引水槽过水横断面应设计为等腰梯形,为了使引水槽的过水流量最大,应使引水槽的横断面面积S为最大,如果设引水槽横断面的等腰梯形的腰长为x,腰与下底的夹角为![]() (如图所示)。
(如图所示)。
(1)试将S表示成关于![]() 和
和![]() 的函数;
的函数;
(2)当![]() 一定时,求S的最大值
一定时,求S的最大值![]() ;
;
(3)当![]() 为何值时,(2)中
为何值时,(2)中![]() 取得最大值,并求出最大值和此时
取得最大值,并求出最大值和此时![]() 的值。
的值。
20.(13分)在正方体骰子的六个面中,有三个面标有数字0,两个面标有数字1,一个面标有数字2, 现同时抛掷三枚骰子.
(1)求三枚骰子出现的数字之积最大的概率;(2)求数字0、1、2各出现一次的概率;(3)求三枚骰子出现的数字之积的分布列与数学期望。
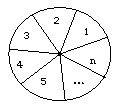
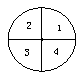
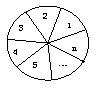
21.(14分)有一种摇奖盘是将一单位圆分成n(![]() )个均匀的扇形区域构成的(如图所示),现需将这n个扇形区域用三种不同颜色涂色,并要求三种颜色都要使用,且相邻的区域不能同色。如果把含有n(
)个均匀的扇形区域构成的(如图所示),现需将这n个扇形区域用三种不同颜色涂色,并要求三种颜色都要使用,且相邻的区域不能同色。如果把含有n(![]() )个扇形区域的摇奖盘的涂色方法数记为
)个扇形区域的摇奖盘的涂色方法数记为![]() 。(1)求:
。(1)求:![]() 、
、![]() ;(2)试用
;(2)试用![]() 、
、![]() 表示
表示![]() (只要求写出关系式);并证明数列
(只要求写出关系式);并证明数列![]() (
(![]() )是等比数列;(3)求数列
)是等比数列;(3)求数列![]() (
(![]() )的通项公式。
)的通项公式。
第Ⅱ卷(答题卷)
二、填空题:
12. ;13. ;14. ;15. 。
三、解答题(注意:答题时不要超出方框)
16.
17.
18.
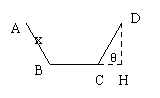 |
19.
20.
 21.
21.

参考答案:
一、选择题 1.A; 2.B ; 3. A ;4. C ; 5. B ;6. D; 7.C ;8.C ; 9.B ; 10.C 11.D .
1.A
2.解析:当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
由B ![]() A
A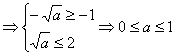
∴a≤1,故选B.
另解: 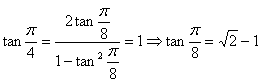 .
.
3. ∵![]() 的解集为R,故选A
的解集为R,故选A
4.解析:思路1:特殊值法,令n=1,则
S1=a1=48,a2=S2-S1=12
∴d=-36 ∴a3=a2+d=-24,
∴S3=48+12-24=36 故选 C
思路2;由![]() 成等差数列,知:
成等差数列,知:
![]()
∴ ![]() 故选 C
故选 C
思路3: 由Sn,S2n-Sn,S3n-S2n成等差数列得:
2(S2n-Sn)=Sn+(S3n-S2n)
得: S3n=3(S2n-Sn)=36 故选 C
5. 解析: ∵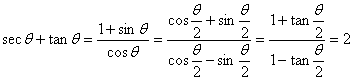
![]() , ∴
, ∴![]()
∴故选B.
6. 解析: 由![]() ,
,
![]()
∴由![]() 的解依次成等差数列,
的解依次成等差数列,
![]() 的解依次成等差数列,
的解依次成等差数列,
![]() ,即a=2或3或4
,即a=2或3或4
故选D.
7. ∵![]() ,∴当
,∴当![]() 时为有理项,又因为
时为有理项,又因为![]() 的展开式共有13项,所以从中任取一项为有理项的概率为
的展开式共有13项,所以从中任取一项为有理项的概率为![]() ,故选C
,故选C
8. 【解析】
∵ ![]()
=![]()
![]()
![]()
![]()
“=”当且仅当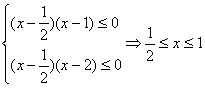 时成立。
时成立。
故选C
9.利用检验法可得B正确
10.解析: ∵方程![]() 的两根分别为x1,x2,
的两根分别为x1,x2,
∴可设:![]()
∵![]() ,
,
∴![]() ,
,![]()
∴![]()
![]()
![]()
![]() 。故选C。
。故选C。
11.解析:方法一:由1![]() 且
且![]()
![]()
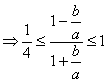 ,记
,记![]() ,
,
则有: ![]()
![]()
![]()
![]()
即![]() 的取值范围是
的取值范围是![]() ;故选D.
;故选D.
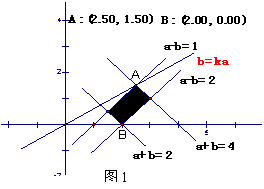
方法二: 由1![]() 且
且![]()
![]() ……(Ⅰ)
……(Ⅰ)
画出不等式组(Ⅰ)表示的可行域, 记![]() ,由图象可知:当直线b=ka过点A时,k取得最大值
,由图象可知:当直线b=ka过点A时,k取得最大值![]() , 当直线b=ka过点B时,k取得最小值0, ∴
, 当直线b=ka过点B时,k取得最小值0, ∴![]() 的取值范围是
的取值范围是![]() ;
;
二、填空题
12. ![]() ;
;
解析:以OA、OB为平行四边形的的边,
作平行四边形OADC,则
![]()
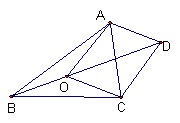 ∵
∵ ![]() ∴
∴![]()
∴![]()
∴![]()
∴![]()
13. 1024;
解析:方法1:由![]() ,两边同时求导得:
,两边同时求导得: ![]() ,令x=0得:
,令x=0得:![]() ;
;
方法2:![]() ,∴
,∴![]()
14.因数列![]() 为等比,则
为等比,则![]() ,因数列
,因数列![]() 也是等比数列,则
也是等比数列,则
![]()
即,![]() ,所以
,所以![]() 。
。
15.![]() ;
;
解析:由![]() 得:
得:
![]() ,则
,则![]()
三、解答题
16. 解:![]() ……2分
……2分
(1)![]()
![]() ……4分
……4分
a<0时,
![]() ……6分
……6分
a=0时![]() 显然不符合条件。
显然不符合条件。
∴![]() 时, a的取值范围是
时, a的取值范围是![]() ……8分
……8分
(2)要满足![]() 时成立
时成立
∵此时B![]()
故所求的a值为3。 ………12分
17.解析:(1)因为![]() 图像关于直线
图像关于直线![]() 对称,
对称,
所以, ![]() , ……2分
, ……2分
即![]() ,所以
,所以![]() ,
,![]()
![]() Z,
Z,
解得![]() ,
,![]()
![]() Z,
Z,
又因为![]() ,故取
,故取![]() 。……4分
。……4分
(2)由(1)![]() ,
,
由![]() ,
,![]() Z……6分
Z……6分
![]()
故f(x)单调减区间为![]() ,
,![]() Z
Z
(注:写成![]() ,
,![]() Z也可)……8分
Z也可)……8分
(3)因为对于连续函数![]() 的图像上任意两点A、B,在图象上总存在一点P,使得过点P的切线斜率等于直线AB的斜率,因此,我们只需求出过
的图像上任意两点A、B,在图象上总存在一点P,使得过点P的切线斜率等于直线AB的斜率,因此,我们只需求出过![]() 的图像上任意一点切线的斜率的取值范围。
的图像上任意一点切线的斜率的取值范围。
由 ![]() ,
,
得:![]() ,……10分
,……10分
∴ ![]() 即曲线切线的斜率的取值范围是[-2,2]
即曲线切线的斜率的取值范围是[-2,2]
∴直线AB的斜率的取值范围[-2,2] ……12分
18.解:(1)∵![]() ,
,
∴![]() 在
在![]() 上恒成立……(2分)
上恒成立……(2分)
∴![]()
∵![]() ,∴
,∴![]()
∴![]() 即a的取值范围为
即a的取值范围为![]() ……(4分)
……(4分)
(2)由![]()
∵当![]() 时,
时,![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ……(7分)
……(7分)
∴![]() ,
,
![]() ……(9分)
……(9分)
(3)∵![]() 有三个不同的实根,
有三个不同的实根,
∴![]() ,
,
![]() ……(12分)
……(12分)
∴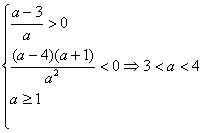
∴a的取值范围为(3,4)……(14分)
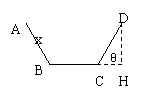 19.解:(1)由题意可知:AB=CD=x,BC=2-2x,上底AD=2-2x+2xcosθ,高DH=xsinθ,
19.解:(1)由题意可知:AB=CD=x,BC=2-2x,上底AD=2-2x+2xcosθ,高DH=xsinθ,
∴![]()
![]()
即![]() ,(
,(![]() )……4分
)……4分
(2)由(1)知:
![]()
=![]()
∴![]() ……8分
……8分
(3)方法1: 由![]()
![]() ,
,
构造点:![]() ,A(2,0),则
,A(2,0),则![]() 为PA的斜率的相反数,由于点P在单位圆上,由几何知识得:
为PA的斜率的相反数,由于点P在单位圆上,由几何知识得: ![]() 时,
时,![]() 取得最大值
取得最大值![]() ……12分
……12分
又因为当![]() 时,
时,![]()
∴当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,此时
,此时![]() 。……14分
。……14分
方法2:记![]()
![]()
![]()
![]()
![]()
![]()
![]() (其中
(其中![]() ,
,![]() )
)
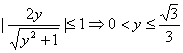
由![]() 得:
得:![]() ,
,
![]() ,
,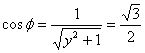
![]() 。∴
。∴![]()
∴![]() ,
,
“=”当且仅当![]() ,
,![]() 时成立,
时成立,
∴当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,此时
,此时![]() 。……14分
。……14分
其它方法酌情给分
20.解析:
(1) 因为三枚骰子出现的数字均为2时其积最大,而每枚骰子出现数字2的概率均为![]() ,∴
,∴![]() ……3分
……3分
(2)∵每枚骰子出现数字0、1、2的概率均分别为![]() 、
、![]() 、
、![]() ,
,
∴数字0、1、2各出现一次的概率为![]() ……7分
……7分
(3)设三枚骰子出现的数字之积为ξ,则ξ=0、1、2、4、8
∵![]()
![]()
![]()
![]()
![]()
∴三枚骰子出现的数字之积的分布列为:
| ξ | 0 | 1 | 2 | 4 | 8 |
| P |
|
|
|
|
|
……11分
数学期望为: ![]() ……13分
……13分
注:求![]() ,利用
,利用![]()
较为方便。

 21.解:
21.解:
(1)![]() ……(2分)
……(2分)
![]() ……(4分)
……(4分)
(2)如果我们在含有n区域的摇奖盘中的某一区域内再插入一个区域(如图3所示),则共有n+2个区域,而此时插入的这个区域有2种涂色方法,故此时n+2个区域共有2![]() 种涂色方法;
种涂色方法;

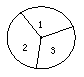
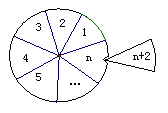 如果我们在含有n+1区域的摇奖盘中的某两个相邻的交界线上再插入一个区域(如图4所示),则共有n+2个区域,而此时插入的这个区域只有1种涂色方法,故此时n+2个区域共有
如果我们在含有n+1区域的摇奖盘中的某两个相邻的交界线上再插入一个区域(如图4所示),则共有n+2个区域,而此时插入的这个区域只有1种涂色方法,故此时n+2个区域共有![]() 种涂色方法;所以:
种涂色方法;所以:
![]() ……(7分)
……(7分)
![]()
![]()
![]()
![]()
∴![]() (
(![]() )是以2为公比的等比数列……(8分)
)是以2为公比的等比数列……(8分)
(3)由(3)可知![]()
![]()
![]()
![]()
![]()
令![]() ,则有
,则有![]() ……(10分)
……(10分)
![]()
![]()
![]() ……(12分)
……(12分)
又∵![]()
∴![]() ,
,
∴![]() ,即
,即![]() (
(![]() )……(14分)
)……(14分)
注: 由![]() ,得出数列
,得出数列![]() 是以
是以![]() 为公比的等比数列,得出
为公比的等比数列,得出![]()
![]()
![]() ,扣2分
,扣2分
其它方法酌情给分